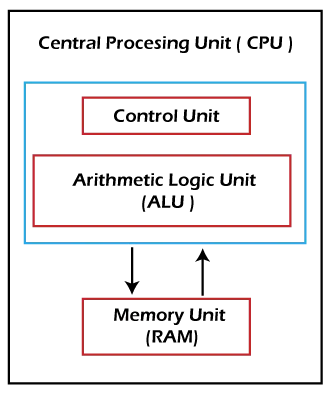
Ukupna pokrivenost svih nula u binarnoj matrici

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } S obzirom na binarnu matricu koja sadrži samo nule i jedinice, trebamo pronaći zbroj pokrivenosti svih nula matrice gdje je pokrivenost za određenu 0 definirana kao ukupni broj jedinica oko nule u smjeru lijevo desno gore i dolje. One mogu biti bilo gdje sve do točke ugla u smjeru.
Primjeri:
Input : mat[][] = {0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0} Output : 20 First four zeros are surrounded by only one 1. So coverage for zeros in first row is 1 + 1 + 1 + 1 Zeros in second row are surrounded by three 1's. Note that there is no 1 above. There are 1's in all other three directions. Coverage of zeros in second row = 3 + 3. Similarly counting for others also we get overall count as below. 1 + 1 + 1 + 1 + 3 + 3 + 2 + 2 + 2 + 2 + 2 = 20 Input : mat[][] = {1 1 1 0 1 0 0 1} Output : 8 Coverage of first zero is 2 Coverages of other two zeros is 3 Total coverage = 2 + 3 + 3 = 8 Recommended Practice Pokrivenost svih nula u binarnoj matrici Probajte! A jednostavno rješenje riješiti ovaj problem je neovisnim prebrojavanjem jedinica oko nula, tj. pokrećemo petlju četiri puta u svakom smjeru za svaku ćeliju za danu matricu. Kad god pronađemo 1 u bilo kojoj petlji, prekidamo petlju i povećavamo rezultat za 1.
An učinkovito rješenje je učiniti sljedeće.
- Prelazi sve retke slijeva na desno, povećava rezultat ako je 1 već viđen (u trenutnom obilasku), a trenutni element je 0.
- Pređite sve retke s desna na lijevo, povećajte rezultat ako je 1 već viđen (u trenutnom obilasku), a trenutni element je 0.
- Pređite sve stupce od vrha do dna, povećajte rezultat ako je 1 već viđen (u trenutnom obilasku), a trenutni element je 0.
- Pređite sve stupce od dna do vrha, povećajte rezultat ako se 1 već vidi (u trenutnom obilasku), a trenutni element je 0.
U donjem kodu uzima se Booleova varijabla isOne koja postaje istinita čim se naiđe na jedinicu u trenutnom obilaženju za sve nule nakon što se taj rezultat iteracije poveća jednom istom procedurom koja se primjenjuje u sva četiri smjera da bi se dobio konačni odgovor. Ponovno postavljamo isOne na false nakon svakog obilaska.
C++ // C++ program to get total coverage of all zeros in // a binary matrix #include using namespace std ; #define R 4 #define C 4 // Returns total coverage of all zeros in mat[][] int getTotalCoverageOfMatrix ( int mat [ R ][ C ]) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { bool isOne = false ; // 1 is not seen yet // looping in columns from left to right // direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we have found // a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for right to // left direction. isOne = false ; for ( int j = C -1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns for up and down // directions. for ( int j = 0 ; j < C ; j ++ ) { bool isOne = false ; // 1 is not seen yet for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R -1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods int main () { int mat [ R ][ C ] = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 } }; cout < < getTotalCoverageOfMatrix ( mat ); return 0 ; }
Java // Java program to get total // coverage of all zeros in // a binary matrix import java . io . * ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage // of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [][] mat ) { int res = 0 ; // looping for all // rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet boolean isOne = false ; // looping in columns from // left to right direction // to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet boolean isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code static public void main ( String [] args ) { int [][] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; System . out . println ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by anuj_67.
Python3 # Python3 program to get total coverage of all zeros in # a binary matrix R = 4 C = 4 # Returns total coverage of all zeros in mat[][] def getTotalCoverageOfMatrix ( mat ): res = 0 # looping for all rows of matrix for i in range ( R ): isOne = False # 1 is not seen yet # looping in columns from left to right # direction to get left ones for j in range ( C ): # If one is found from left if ( mat [ i ][ j ] == 1 ): isOne = True # If 0 is found and we have found # a 1 before. else if ( isOne ): res += 1 # Repeat the above process for right to # left direction. isOne = False for j in range ( C - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 # Traversing across columns for up and down # directions. for j in range ( C ): isOne = False # 1 is not seen yet for i in range ( R ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 isOne = False for i in range ( R - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 return res # Driver code mat = [[ 0 0 0 0 ][ 1 0 0 1 ][ 0 1 1 0 ][ 0 1 0 0 ]] print ( getTotalCoverageOfMatrix ( mat )) # This code is contributed by shubhamsingh10
C# // C# program to get total coverage // of all zeros in a binary matrix using System ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [] mat ) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet bool isOne = false ; // looping in columns from left to // right direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for // right to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet bool isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods static public void Main () { int [] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; Console . WriteLine ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by vt_m.
JavaScript < script > // Javascript program to get total // coverage of all zeros in // a binary matrix let R = 4 ; let C = 4 ; // Returns total coverage // of all zeros in mat[][] function getTotalCoverageOfMatrix ( mat ) { let res = 0 ; // looping for all // rows of matrix for ( let i = 0 ; i < R ; i ++ ) { // 1 is not seen yet let isOne = false ; // looping in columns from // left to right direction // to get left ones for ( let j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( let j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( let j = 0 ; j < C ; j ++ ) { // 1 is not seen yet let isOne = false ; for ( let i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( let i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } let mat = [[ 0 0 0 0 ] [ 1 0 0 1 ] [ 0 1 1 0 ] [ 0 1 0 0 ]]; document . write ( getTotalCoverageOfMatrix ( mat )); < /script>
Izlaz
20
Vremenska složenost: O(n 2 )
Pomoćni prostor: O(1)
Napravi kviz