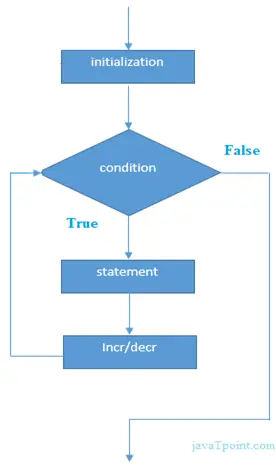
Un nombre est dit heureux s'il mène à 1 après une séquence d'étapes dans laquelle chaque numéro d'étape est remplacé par la somme des carrés de son chiffre, c'est-à-dire que si nous commençons par Happy Number et continuons à le remplacer par la somme carrée des chiffres, nous atteignons 1. 

Exemples :  

 Input: n = 19   
 Output: True   
 19 is Happy Number   
 1^2 + 9^2 = 82   
 8^2 + 2^2 = 68   
 6^2 + 8^2 = 100   
 1^2 + 0^2 + 0^2 = 1   
 As we reached to 1 19 is a Happy Number.   
  
 Input: n = 20   
 Output: False  
   
 C++   
   // method return true if n is Happy Number   int     numSquareSum  (  int     n  )     {      int     num     =     0  ;      while     (  n     !=     0  )     {      int     digit     =     n     %     10  ;      num     +=     digit     *     digit  ;      n     /=     10  ;      }      return     num  ;   }   int     isHappyNumber  (  int     n  )   {      set   <  int  >     st  ;      while     (  1  )      {      n     =     numSquareSum  (  n  );      if     (  n     ==     1  )      return     true  ;      if     (  st  .  find  (  n  )     !=     st  .  end  ())      return     false  ;      st  .  insert  (  n  );      }   }   
  Java   
   // method return true if n is Happy Number   public     static     int     numSquareSum  (  int     n  )   {      int     num     =     0  ;      while     (  n     !=     0  )     {      int     digit     =     n     %     10  ;      num     +=     digit     *     digit  ;      n     /=     10  ;      }      return     num  ;   }   static     boolean     isHappyNumber  (  int     n  )   {      HashSet   <  Integer  >     st     =     new     HashSet   <>  ();      while     (  true  )     {      n     =     numSquareSum  (  n  );      if     (  n     ==     1  )      return     true  ;      if     (  st  .  contains  (  n  ))      return     false  ;      st  .  add  (  n  );      }   }   // This code is contributed by Princi Singh   
  Python   
   # method return true if n is Happy Number   def   numSquareSum  (  n  ):   num   =   0   while  (  n  ):   digit   =   n   %   10   num   =   num   +   digit  *  digit   n   =   n   //   10   return   num   def   isHappyNumber  (  n  ):   st   =   set  ()   while   (  1  ):   n   =   numSquareSum  (  n  )   if   (  n   ==   1  ):   return   True   if   n   not   in   st  :   return   False   st  .  insert  (  n  )   
  C#   
   // Method return true if n is Happy Number   static     int     numSquareSum  (  int     n  )   {      int     num     =     0  ;      while     (  n     !=     0  )     {      int     digit     =     n     %     10  ;      num     +=     digit     *     digit  ;      n     /=     10  ;      }      return     num  ;   }   static     int     isHappyNumber  (  int     n  )   {      HashSet   <  int  >     st     =     new     HashSet   <>  ();      while     (  1  )     {      n     =     numSquareSum  (  n  );      if     (  n     ==     1  )      return     true  ;      if     (  st  .  Contains  (  n  ))      return     false  ;      st  .  Add  (  n  );      }   }   // This code is contributed by 29AjayKumar   
  JavaScript   
    <  script  >   // method return true if n is Happy Number      function     numSquareSum  (  n  )     {      let     num     =     0  ;      while     (  n     !==     0  )     {      let     digit     =     n     %     10  ;      num     +=     digit     *     digit  ;      n     =     Math  .  floor  (  n     /     10  );      }      return     num  ;      }      let     st     =     new     Set  ();      while     (  1  )      {      n     =     numSquareSum  (  n  );      if     (  n     ==     1  )      return     true  ;      if     (  st  .  has  (  n  ))      return     false  ;      st  .  add  (  n  );      }   }   //This code is contributed by Mayank Tyagi    <  /script>   
   
    Analyse de complexité :    
 
    Complexité temporelle :    O(n*log(n)).    
    Espace auxiliaire :    O(n) depuis l'utilisation d'un ensemble supplémentaire pour le stockage  
 
 Nous pouvons résoudre ce problème sans utiliser d’espace supplémentaire et cette technique peut également être utilisée dans d’autres problèmes similaires. Si nous traitons chaque nombre comme un nœud et le remplaçons par un chiffre de somme carrée comme un lien, alors ce problème est le même que    trouver une boucle dans une liste de liens    :   
 
 Ainsi, comme solution proposée à partir du lien ci-dessus, nous garderons deux nombres lents et rapides, tous deux initialisés à partir d'un nombre donné, lent est remplacé une étape à la fois et rapide est remplacé deux étapes à la fois. If they meet at 1 then the given number is Happy Number otherwise not.    
 C++   
   // C++ program to check a number is a Happy number or not   #include          using     namespace     std  ;   // Utility method to return sum of square of digit of n   int     numSquareSum  (  int     n  )   {      int     squareSum     =     0  ;      while     (  n  )     {      squareSum     +=     (  n     %     10  )     *     (  n     %     10  );      n     /=     10  ;      }      return     squareSum  ;   }   // method return true if n is Happy number   bool     isHappynumber  (  int     n  )   {      int     slow       fast  ;      // initialize slow and fast by n      slow     =     fast     =     n  ;      do     {      // move slow number by one iteration      slow     =     numSquareSum  (  slow  );      // move fast number by two iteration      fast     =     numSquareSum  (  numSquareSum  (  fast  ));      }     while     (  slow     !=     fast  );      // if both number meet at 1 then return true      return     (  slow     ==     1  );   }   // Driver code to test above methods   int     main  ()   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      cout      < <     n      < <     ' is a Happy number  n  '  ;      else      cout      < <     n      < <     ' is not a Happy number  n  '  ;   }   // This code is contributed by divyeshrabadiya07   
  C   
   // C program to check a number is a Happy number or not   #include         #include         // Utility method to return sum of square of digit of n   int     numSquareSum  (  int     n  )   {      int     squareSum     =     0  ;      while     (  n  )     {      squareSum     +=     (  n     %     10  )     *     (  n     %     10  );      n     /=     10  ;      }      return     squareSum  ;   }   // method return true if n is Happy number   bool     isHappynumber  (  int     n  )   {      int     slow       fast  ;      // initialize slow and fast by n      slow     =     fast     =     n  ;      do     {      // move slow number by one iteration      slow     =     numSquareSum  (  slow  );      // move fast number by two iteration      fast     =     numSquareSum  (  numSquareSum  (  fast  ));      }     while     (  slow     !=     fast  );      // if both number meet at 1 then return true      return     (  slow     ==     1  );   }   // Driver code to test above methods   int     main  ()   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      printf  (  '%d is a Happy number  n  '       n  );      else      printf  (  '%d is not a Happy number  n  '       n  );   }   // This code is contributed by Sania Kumari Gupta   // (kriSania804)   
  Java   
   // Java program to check a number is a Happy   // number or not   class   GFG     {       // Utility method to return sum of square of   // digit of n   static     int     numSquareSum  (  int     n  )   {      int     squareSum     =     0  ;      while     (  n  !=     0  )      {      squareSum     +=     (  n     %     10  )     *     (  n     %     10  );      n     /=     10  ;      }      return     squareSum  ;   }       // method return true if n is Happy number   static     boolean     isHappynumber  (  int     n  )   {      int     slow       fast  ;          // initialize slow and fast by n      slow     =     fast     =     n  ;      do      {      // move slow number      // by one iteration      slow     =     numSquareSum  (  slow  );          // move fast number      // by two iteration      fast     =     numSquareSum  (  numSquareSum  (  fast  ));          }      while     (  slow     !=     fast  );          // if both number meet at 1      // then return true      return     (  slow     ==     1  );   }       // Driver code to test above methods   public     static     void     main  (  String  []     args  )   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      System  .  out  .  println  (  n     +         ' is a Happy number'  );      else      System  .  out  .  println  (  n     +         ' is not a Happy number'  );   }   }   
  Python   
   # Python3 program to check if a number is a Happy number or not   # Utility method to return the sum of squares of digits of n   def   num_square_sum  (  n  ):   square_sum   =   0   while   n  :   square_sum   +=   (  n   %   10  )   **   2   n   //=   10   return   square_sum   # Method returns True if n is a Happy number   def   is_happy_number  (  n  ):   # Initialize slow and fast pointers   slow   =   n   fast   =   n   while   True  :   # Move slow pointer by one iteration   slow   =   num_square_sum  (  slow  )   # Move fast pointer by two iterations   fast   =   num_square_sum  (  num_square_sum  (  fast  ))   if   slow   !=   fast  :   continue   else  :   break   # If both pointers meet at 1 then return True   return   slow   ==   1   # Driver Code   n   =   13   if   is_happy_number  (  n  ):   print  (  n     'is a Happy number'  )   else  :   print  (  n     'is not a Happy number'  )   
  C#   
   // C# program to check a number   // is a Happy number or not   using     System  ;   class     GFG     {   // Utility method to return    // sum of square of digit of n   static     int     numSquareSum  (  int     n  )   {      int     squareSum     =     0  ;      while     (  n  !=     0  )      {      squareSum     +=     (  n     %     10  )     *         (  n     %     10  );      n     /=     10  ;      }      return     squareSum  ;   }   // method return true if   // n is Happy number   static     bool     isHappynumber  (  int     n  )   {      int     slow       fast  ;      // initialize slow and      // fast by n      slow     =     fast     =     n  ;      do      {          // move slow number      // by one iteration      slow     =     numSquareSum  (  slow  );      // move fast number      // by two iteration      fast     =     numSquareSum  (  numSquareSum  (  fast  ));      }      while     (  slow     !=     fast  );      // if both number meet at 1      // then return true      return     (  slow     ==     1  );   }   // Driver code   public     static     void     Main  ()   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      Console  .  WriteLine  (  n     +         ' is a Happy number'  );      else      Console  .  WriteLine  (  n     +         ' is not a Happy number'  );   }   }   // This code is contributed by anuj_67.   
  JavaScript   
    <  script  >   // Javascript program to check a number is a Happy   // number or not   // Utility method to return sum of square of   // digit of n   function     numSquareSum  (  n  )   {      var     squareSum     =     0  ;      while     (  n  !=     0  )      {      squareSum     +=     (  n     %     10  )     *     (  n     %     10  );      n     =     parseInt  (  n  /  10  );      }      return     squareSum  ;   }       // method return true if n is Happy number   function     isHappynumber  (  n  )   {      var     slow       fast  ;          // initialize slow and fast by n      slow     =     fast     =     n  ;      do      {      // move slow number      // by one iteration      slow     =     numSquareSum  (  slow  );          // move fast number      // by two iteration      fast     =     numSquareSum  (  numSquareSum  (  fast  ));          }      while     (  slow     !=     fast  );          // if both number meet at 1      // then return true      return     (  slow     ==     1  );   }       // Driver code to test above methods   var     n     =     13  ;   if     (  isHappynumber  (  n  ))      document  .  write  (  n     +         ' is a Happy number'  );   else      document  .  write  (  n     +         ' is not a Happy number'  );       // This code contributed by Princi Singh     <  /script>   
  PHP   
      // PHP program to check a number   // is a Happy number or not   // Utility method to return    // sum of square of digit of n   function   numSquareSum  (   $n  )   {   $squareSum   =   0  ;   while   (  $n  )   {   $squareSum   +=   (  $n   %   10  )   *   (  $n   %   10  );   $n   /=   10  ;   }   return   $squareSum  ;   }   // method return true if   // n is Happy number   function   isHappynumber  (   $n  )   {   $slow  ;   $fast  ;   // initialize slow    // and fast by n   $slow   =   $n  ;   $fast   =   $n  ;   do   {   // move slow number   // by one iteration   $slow   =   numSquareSum  (  $slow  );   // move fast number   // by two iteration   $fast   =   numSquareSum  (  numSquareSum  (  $fast  ));   }   while   (  $slow   !=   $fast  );   // if both number meet at 1    // then return true   return   (  $slow   ==   1  );   }   // Driver Code   $n   =   13  ;   if   (  isHappynumber  (  $n  ))   echo   $n      ' is a Happy number  n  '  ;   else   echo   n      ' is not a Happy number  n  '  ;   // This code is contributed by anuj_67.   ?>   
   
    Sortir :       
 
 13 is a Happy Number  
    Analyse de complexité :    
 
    Complexité temporelle :    O(n*log(n)).   
    Espace auxiliaire :      
 
  
    Une autre approche pour résoudre ce problème sans utiliser d'espace supplémentaire.     
 Un nombre ne peut pas être un nombre heureux     si à n'importe quelle étape la somme des carrés des chiffres obtenus est un nombre à un chiffre sauf 1 ou 7    . This is because 1 and 7 are the only single-digit happy numbers. Using this information we can develop an approach as shown in the code below -   
 C++   
   // C++ program to check if a number is a Happy number or   // not.   #include          using     namespace     std  ;   // Method - returns true if the input is a happy number else   // returns false   bool     isHappynumber  (  int     n  )   {      int     sum     =     n       x     =     n  ;      // This loop executes till the sum of square of digits      // obtained is not a single digit number      while     (  sum     >     9  )     {      sum     =     0  ;      // This loop finds the sum of square of digits      while     (  x     >     0  )     {      int     d     =     x     %     10  ;      sum     +=     d     *     d  ;      x     /=     10  ;      }      x     =     sum  ;      }      if     (  sum     ==     7     ||     sum     ==     1  )      return     true  ;      return     false  ;   }   int     main  ()   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      cout      < <     n      < <     ' is a Happy number'  ;      else      cout      < <     n      < <     ' is not a Happy number'  ;      return     0  ;   }   // This code is contributed by Sania Kumari Gupta   
  C   
   // C program to check if a number is a Happy number or   // not.   #include         #include         // Method - returns true if the input is a happy number else   // returns false   bool     isHappynumber  (  int     n  )   {      int     sum     =     n       x     =     n  ;      // This loop executes till the sum of square of digits      // obtained is not a single digit number      while     (  sum     >     9  )     {      sum     =     0  ;      // This loop finds the sum of square of digits      while     (  x     >     0  )     {      int     d     =     x     %     10  ;      sum     +=     d     *     d  ;      x     /=     10  ;      }      x     =     sum  ;      }      if     (  sum     ==     7     ||     sum     ==     1  )      return     true  ;      return     false  ;   }   int     main  ()   {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      printf  (  '%d is a Happy number'       n  );      else      printf  (  '%d is not a Happy number'       n  );      return     0  ;   }   // This code is contributed by Sania Kumari Gupta   
  Java   
   // This code is contributed by Vansh Sodhi.   // Java program to check if a number is a Happy number or   // not.   class   GFG     {      // method - returns true if the input is a happy      // number else returns false      static     boolean     isHappynumber  (  int     n  )      {      int     sum     =     n       x     =     n  ;      // this loop executes till the sum of square of      // digits obtained is not a single digit number      while     (  sum     >     9  )     {      sum     =     0  ;      // this loop finds the sum of square of digits      while     (  x     >     0  )     {      int     d     =     x     %     10  ;      sum     +=     d     *     d  ;      x     /=     10  ;      }      x     =     sum  ;      }      if     (  sum     ==     1     ||     sum     ==     7  )      return     true  ;      return     false  ;      }      // Driver code      public     static     void     main  (  String  []     args  )      {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      System  .  out  .  println  (  n     +     ' is a Happy number'  );      else      System  .  out  .  println  (  n      +     ' is not a Happy number'  );      }   }   
  Python   
   # Python3 program to check if a number is a Happy number or not.   # Method - returns true if the input is   # a happy number else returns false   def   isHappynumber  (  n  ):   Sum     x   =   n     n   # This loop executes till the sum   # of square of digits obtained is   # not a single digit number   while   Sum   >   9  :   Sum   =   0   # This loop finds the sum of   # square of digits   while   x   >   0  :   d   =   x   %   10   Sum   +=   d   *   d   x   =   int  (  x   /   10  )   x   =   Sum   if   Sum   ==   1   or   Sum   ==   7  :   return   True   return   False   n   =   13   if   isHappynumber  (  n  ):   print  (  n     'is a Happy number'  )   else  :   print  (  n     'is not a Happy number'  )   # This code is contributed by mukesh07.   
  C#   
   // C# program to check if a number   // is a Happy number or not.   using     System  ;   class     GFG     {      // Method - returns true if the input is      // a happy number else returns false      static     bool     isHappynumber  (  int     n  )      {      int     sum     =     n       x     =     n  ;      // This loop executes till the sum      // of square of digits obtained is      // not a single digit number      while     (  sum     >     9  )     {      sum     =     0  ;      // This loop finds the sum of      // square of digits      while     (  x     >     0  )     {      int     d     =     x     %     10  ;      sum     +=     d     *     d  ;      x     /=     10  ;      }      x     =     sum  ;      }      if     (  sum     ==     1     ||     sum     ==     7  )      return     true  ;      return     false  ;      }      // Driver code      public     static     void     Main  (  String  []     args  )      {      int     n     =     13  ;      if     (  isHappynumber  (  n  ))      Console  .  WriteLine  (  n     +     ' is a Happy number'  );      else      Console  .  WriteLine  (  n     +     ' is not a Happy number'  );      }   }   // This code is contributed by 29AjayKumar   
  JavaScript   
    <  script  >   // This code is contributed by Vansh Sodhi.   // javascript program to check if a number is a Happy number or not.      // method - returns true if the input is a happy      // number else returns false      function     isHappynumber  (  n  )      {      var     sum     =     n       x     =     n  ;      // this loop executes till the sum of square of      // digits obtained is not a single digit number      while  (  sum     >     9  )         {      sum     =     0  ;      // this loop finds the sum of square of digits      while     (  x     >     0  )         {      var     d     =     x     %     10  ;      sum     +=     d     *     d  ;      x     /=     10  ;      }      x     =     sum  ;      }      if  (  sum     ==     1     ||     sum     ==     7  )      return     true  ;      return     false  ;   }   // Driver code      var     n     =     13  ;      if     (  isHappynumber  (  n  ))      document  .  write  (  n     +         ' is a Happy number'  );      else      document  .  write  (  n     +         ' is not a Happy number'  );       // This code is contributed by 29AjayKumar     <  /script>   
    
  Sortir   
13 is a Happy number 
 
    Analyse de complexité :    
 
    Complexité temporelle :    O(n*log(n)).   
    Espace auxiliaire :    O(1).   
 
 Consultez votre article apparaissant sur la page principale de GeeksforGeeks et aidez les autres Geeks.