Edellytys: Lineaarinen regressio

Lineaarinen regressio on koneoppimisalgoritmi, joka perustuu valvottuun oppimiseen. Se suorittaa regressiotehtävän. Regressio mallintaa tavoiteennustusarvon riippumattomien muuttujien perusteella. Sitä käytetään enimmäkseen muuttujien ja ennustamisen välisen suhteen selvittämiseen. Erilaiset regressiomallit eroavat toisistaan ​​sen mukaan, millainen riippuvaisten ja riippumattomien muuttujien välinen suhde, mitä ne harkitsevat ja kuinka monta riippumatonta muuttujaa käytetään. Tämä artikkeli osoittaa, kuinka käyttää erilaisia ​​Python-kirjastoja lineaarisen regression toteuttamiseen tietyssä tietojoukossa. Esitämme binaarisen lineaarisen mallin, koska se on helpompi visualisoida. Tässä esittelyssä malli käyttää Gradient Descent -tekniikkaa oppimiseen. Voit oppia siitä täältä.

Vaihe 1: Tuodaan kaikki tarvittavat kirjastot

Python 3

import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn> import> preprocessing, svm> from> sklearn.model_selection> import> train_test_split> from> sklearn.linear_model> import> LinearRegression>

Vaihe 2: Tietojoukon lukeminen:

Python 3

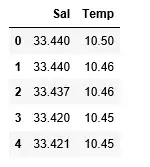
df> => pd.read_csv(> 'bottle.csv'> )> df_binary> => df[[> 'Salnty'> ,> 'T_degC'> ]]> > # Taking only the selected two attributes from the dataset> df_binary.columns> => [> 'Sal'> ,> 'Temp'> ]> #display the first 5 rows> df_binary.head()>

Lähtö:

Vaihe 3: Tiedonhajannan tutkiminen

Python 3

#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary, order> => 2> , ci> => None> )> plt.show()>

Lähtö:

Vaihe 4: Tietojen puhdistus

Python 3

# Eliminating NaN or missing input numbers> df_binary.fillna(method> => 'ffill'> , inplace> => True> )>

Vaihe 5: Koulutamme malliamme

Python 3

X> => np.array(df_binary[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace> => True> )> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > # Splitting the data into training and testing data> regr> => LinearRegression()> > regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Lähtö:

Vaihe 6: Tutkimme tuloksiamme

Python 3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()> # Data scatter of predicted values>

Lähtö:

Mallimme alhainen tarkkuuspistemäärä viittaa siihen, että regressiivinen mallimme ei ole sopinut kovin hyvin olemassa olevaan dataan. Tämä viittaa siihen, että tietomme eivät sovellu lineaariseen regressioon. Mutta joskus tietojoukko voi hyväksyä lineaarisen regressorin, jos otamme huomioon vain osan siitä. Tarkastellaanpa tätä mahdollisuutta.

Vaihe 7: Työskentely pienemmän tietojoukon kanssa

Python 3

df_binary500> => df_binary[:][:> 500> ]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary500,> > order> => 2> , ci> => None> )>

Lähtö:

Voimme jo nähdä, että ensimmäiset 500 riviä noudattavat lineaarista mallia. Jatka samalla tavalla kuin ennenkin.

Python 3

df_binary500.fillna(method> => 'fill'> , inplace> => True> )> > X> => np.array(df_binary500[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary500[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > df_binary500.dropna(inplace> => True> )> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > regr> => LinearRegression()> regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Lähtö:

Python 3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()>

Lähtö:

Vaihe 8: Regression arviointimetrit

Lopuksi tarkistamme Lineaarisen regressiomallin suorituskyvyn arviointimetriikan avulla. Regressioalgoritmeissa käytämme laajalti keskiarvo_absoluuttinen_virhe- ja keskimääräinen_neliövirhe -mittauksia mallin suorituskyvyn tarkistamiseen.

Python 3

from> sklearn.metrics> import> mean_absolute_error,mean_squared_error> > mae> => mean_absolute_error(y_true> => y_test,y_pred> => y_pred)> #squared True returns MSE value, False returns RMSE value.> mse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred)> #default=True> rmse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred,squared> => False> )> > print> (> 'MAE:'> ,mae)> print> (> 'MSE:'> ,mse)> print> (> 'RMSE:'> ,rmse)>

Lähtö:

MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078