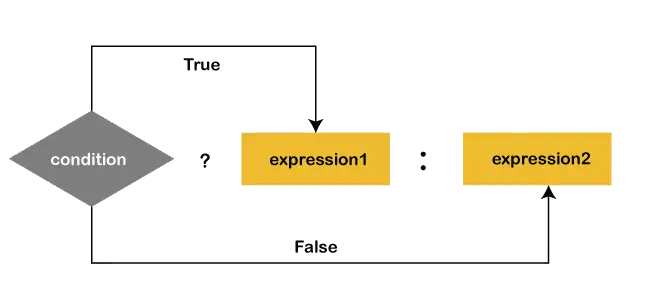
POSTORDER TRAVERSAL OF BINARY TREE

Postimääräyksen läpikulku määritellään tyypiksi puun läpikulku joka noudattaa vasen-oikea-juurikäytäntöä siten, että jokaiselle solmulle:

Vasen alipuu ajetaan ensin

Sitten ajetaan oikea alipuu

Lopuksi alipuun juurisolmu ajetaan

Postimääräyksen läpikulku

Algoritmi binaaripuun postorder-läpikulkuun:

Algoritmi jälkikäteen tapahtuvalle läpikäymiselle on esitetty seuraavasti:

Postimääräys (juuri):

Noudata vaiheita 2–4, kunnes root != NULL

Postorder (juuri -> vasen)

Postorder (juuri -> oikealle)

Kirjoita root -> data

Lopeta silmukka

Kuinka postorder Traversal of Binary Tree toimii?

Harkitse seuraavaa puuta:

Esimerkki binaaripuusta

Jos suoritamme postorder-läpikulun tässä binääripuussa, läpikulku on seuraava:

Vaihe 1: Läpikulku siirtyy luvusta 1 sen vasempaan alipuuhun eli 2:een, sitten 2:sta vasempaan alipuun juureen, eli 4. Nyt 4:llä ei ole alipuuta, joten siinä käydään.

Solmussa 4 käydään

Vaihe 2: Koska 2:n vasemmassa alipuussa käydään kokonaan, se nyt kulkee 2:n oikean alipuun läpi, eli se siirtyy kohtaan 5. Koska luvun 5 alipuuta ei ole, siinä käydään.

Node 5 on vierailtu

Vaihe 3: Nyt käydään sekä solmun 2 vasemmalla että oikealla alipuulla. Joten käy nyt itse solmussa 2.

Node 2 on vierailtu

Vaihe 4: Kun solmun 1 vasen alipuu ajetaan, se siirtyy nyt oikeaan alipuun juureen, eli 3. Solmussa 3 ei ole vasenta alipuuta, joten se kulkee oikean alipuun läpi eli 6. Solmussa 6 ei ole alipuuta ja joten siinä vierailee.

Solmussa 6 käydään

Vaihe 5: Kaikki solmun 3 alipuut kulkevat läpi. Joten nyt solmu 3 on vierailtu.

Solmussa 3 käydään

Vaihe 6: Koska kaikki solmun 1 alipuut kulkevat, on nyt aika käydä solmussa 1 ja läpikulku päättyy sen jälkeen, kun koko puu on ajettu läpi.

Koko puussa käydään

Joten solmujen läpikulkujärjestys on 4 -> 5 -> 2 -> 6 -> 3 -> 1 .

Ohjelma toteuttaa postorder Traversal of Binary Tree

Alla on postorder traversalin kooditoteutus:

C++

// C++ program for postorder traversals> #include> using> namespace> std;> // Structure of a Binary Tree Node> struct> Node {> > int> data;> > struct> Node *left, *right;> > Node(> int> v)> > {> > data = v;> > left = right = NULL;> > }> };> // Function to print postorder traversal> void> printPostorder(> struct> Node* node)> {> > if> (node == NULL)> > return> ;> > // First recur on left subtree> > printPostorder(node->vasemmalle);> > // Then recur on right subtree> > printPostorder(node->oikealla);> > // Now deal with the node> >

cout ' '; } // Driver code int main() {  struct Node* root = new Node(1);  root->vasen = uusi solmu(2);  juuri->oikea = uusi solmu(3);  juuri->vasen->vasen = uusi solmu(4);  juuri->vasen->oikea = uusi solmu(5);  juuri->oikea->oikea = uusi solmu(6);  // Funktion kutsu < < 'Postorder traversal of binary tree is: 
';  printPostorder(root);  return 0; }>

Java

// Java program for postorder traversals> import> java.util.*;> // Structure of a Binary Tree Node> class> Node {> > int> data;> > Node left, right;> > Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> class> GFG {> > > // Function to print postorder traversal> > static> void> printPostorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > System.out.print(node.data +> ' '> );> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > Node root => new> Node(> 1> );> > root.left => new> Node(> 2> );> > root.right => new> Node(> 3> );> > root.left.left => new> Node(> 4> );> > root.left.right => new> Node(> 5> );> > root.right.right => new> Node(> 6> );> > // Function call> > System.out.println(> 'Postorder traversal of binary tree is: '> );> > printPostorder(root);> > }> }> // This code is contributed by prasad264>

Python 3

# Python program for postorder traversals> # Structure of a Binary Tree Node> class> Node:> > def> __init__(> self> , v):> > self> .data> => v> > self> .left> => None> > self> .right> => None> # Function to print postorder traversal> def> printPostorder(node):> > if> node> => => None> :> > return> > # First recur on left subtree> > printPostorder(node.left)> > # Then recur on right subtree> > printPostorder(node.right)> > # Now deal with the node> > print> (node.data, end> => ' '> )> # Driver code> if> __name__> => => '__main__'> :> > root> => Node(> 1> )> > root.left> => Node(> 2> )> > root.right> => Node(> 3> )> > root.left.left> => Node(> 4> )> > root.left.right> => Node(> 5> )> > root.right.right> => Node(> 6> )> > # Function call> > print> (> 'Postorder traversal of binary tree is:'> )> > printPostorder(root)>

C#

// C# program for postorder traversals> using> System;> // Structure of a Binary Tree Node> public> class> Node {> > public> int> data;> > public> Node left, right;> > public> Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> public> class> GFG {> > // Function to print postorder traversal> > static> void> printPostorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > Console.Write(node.data +> ' '> );> > }> > static> public> void> Main()> > {> > // Code> > Node root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > Console.WriteLine(> > 'Postorder traversal of binary tree is: '> );> > printPostorder(root);> > }> }> // This code is contributed by karthik.>

Javascript

// Structure of a Binary Tree Node> class Node {> > constructor(v) {> > this> .data = v;> > this> .left => null> ;> > this> .right => null> ;> > }> }> // Function to print postorder traversal> function> printPostorder(node) {> > if> (node ==> null> ) {> > return> ;> > }> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > console.log(node.data +> ' '> );> }> // Driver code> function> main() {> > let root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > console.log(>

'Postorder traversal of binary tree is: 
'>

);> > printPostorder(root);> }> main();>

Lähtö

Postorder traversal of binary tree is: 4 5 2 6 3 1

Selitys:

Miten postimyynnin läpikulku toimii

Monimutkaisuusanalyysi:

Aika monimutkaisuus: O(N) missä N on solmujen kokonaismäärä. Koska se kulkee kaikkien solmujen läpi vähintään kerran.
Aputila: O(1), jos rekursiopinotilaa ei oteta huomioon. Muussa tapauksessa O(h), missä h on puun korkeus

Pahimmassa tapauksessa h voi olla sama kuin N (kun puu on vinossa puu)
Parhaassa tapauksessa h voi olla sama kuin rauhoittaa (kun puu on täydellinen puu)