Maksimoi N X N ylävasemman alimatriisin summa annetusta 2N X 2N matriisista

Koska a 2N x 2N kokonaislukumatriisi. Voit kääntää mitä tahansa riviä tai saraketta kuinka monta kertaa tahansa ja missä tahansa järjestyksessä. Tehtävänä on laskea vasemman yläkulman maksimisumma N X N alimatriisi eli alimatriisin elementtien summa välillä (0 0) arvoon (N - 1 N - 1).
Esimerkkejä:
Syöte: kanssa[][] = {
112 42 83 119
56 125 56 49
15 78 101 43
62 98 114 108
}
Lähtö: 414
Annettu matriisi on kooltaan 4 x 4, joka meidän on maksimoitava
vasemman yläkulman 2 x 2 matriisin summa eli
mat[0][0] + matto[0][1] + matto[1][0] + matto[1][1].
Seuraavat toiminnot maksimoivat summan:
1. Käännä sarake 2 toisinpäin
112 42 114 119
56 125 101 49
15 78 56 43
62 98 83 108
2. Käänteinen rivi 0
119 114 42 112
56 125 101 49
15 78 56 43
62 98 83 108
Vasemman ylämatriisin summa = 119 + 114 + 56 + 125 = 414.
Vasemman yläosan alimatriisin summan maksimoimiseksi kunkin ylävasemman alimatriisin solun kohdalla on neljä ehdokasta, mikä tarkoittaa vastaavia soluja ylhäällä vasemmalla-oikealla-ala-vasemmalla ja alaoikealla-alimatriisissa, joiden kanssa se voidaan vaihtaa.
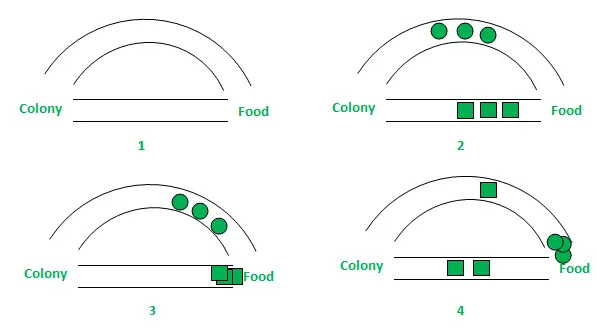
Tarkkaile nyt jokaista solua missä tahansa, voimme vaihtaa sen vasemman yläosan alimatriisin vastaavaan ehdokasarvoon muuttamatta muiden solujen järjestystä vasemman yläosan alimatriisissa. Kaavio näyttää tapauksen, jossa neljän ehdokkaan maksimiarvo on oikean yläkulman alimatriisissa. Jos se on vasemmassa tai alakulmassa, voimme ensin kääntää rivin tai sarakkeen päinvastaiseksi sijoittaaksemme sen oikeaan yläosamatriisiin ja noudattaa sitten samaa toimintosarjaa kuin kaaviossa on esitetty.
Tässä matriisissa sanotaan a 26 on neljän ehdokkaan enimmäismäärä ja a 23 täytyy vaihtaa a:lla 26 muuttamatta solujen järjestystä vasemman yläosan alimatriisissa.

Käänteinen rivi 2

Käänteinen sarake 2

Käänteinen rivi 7

Käänteinen sarake 6

Käänteinen rivi 2

Alla on tämän lähestymistavan toteutus:
C++ // C++ program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations #include #define R 4 #define C 4 using namespace std ; int maxSum ( int mat [ R ][ C ]) { int sum = 0 ; for ( int i = 0 ; i < R / 2 ; i ++ ) for ( int j = 0 ; j < C / 2 ; j ++ ) { int r1 = i ; int r2 = R - i - 1 ; int c1 = j ; int c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += max ( max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])); } return sum ; } // Driven Program int main () { int mat [ R ][ C ] = { 112 42 83 119 56 125 56 49 15 78 101 43 62 98 114 108 }; cout < < maxSum ( mat ) < < endl ; return 0 ; }
Java // Java program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations class GFG { static int maxSum ( int mat [][] ) { int sum = 0 ; int maxI = mat . length ; int maxIPossible = maxI - 1 ; int maxJ = mat [ 0 ] . length ; int maxJPossible = maxJ - 1 ; for ( int i = 0 ; i < maxI / 2 ; i ++ ) { for ( int j = 0 ; j < maxJ / 2 ; j ++ ) { // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . max ( Math . max ( mat [ i ][ j ] mat [ maxIPossible - i ][ j ] ) Math . max ( mat [ maxIPossible - i ] [ maxJPossible - j ] mat [ i ][ maxJPossible - j ] )); } } return sum ; } // Driven Program public static void main ( String [] args ) { int mat [][] = { { 112 42 83 119 } { 56 125 56 49 } { 15 78 101 43 } { 62 98 114 108 } }; System . out . println ( maxSum ( mat )); } } /* This Java code is contributed by Rajput-Ji*/
Python3 # Python3 program to find the maximum value # of top N/2 x N/2 matrix using row and # column reverse operations def maxSum ( mat ): Sum = 0 for i in range ( 0 R // 2 ): for j in range ( 0 C // 2 ): r1 r2 = i R - i - 1 c1 c2 = j C - j - 1 # We can replace current cell [i j] # with 4 cells without changing/affecting # other elements. Sum += max ( max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])) return Sum # Driver Code if __name__ == '__main__' : R = C = 4 mat = [[ 112 42 83 119 ] [ 56 125 56 49 ] [ 15 78 101 43 ] [ 62 98 114 108 ]] print ( maxSum ( mat )) # This code is contributed # by Rituraj Jain
C# // C# program to find maximum value // of top N/2 x N/2 matrix using row // and column reverse operations using System ; class GFG { static int R = 4 ; static int C = 4 ; static int maxSum ( int [ ] mat ) { int sum = 0 ; for ( int i = 0 ; i < R / 2 ; i ++ ) { for ( int j = 0 ; j < C / 2 ; j ++ ) { int r1 = i ; int r2 = R - i - 1 ; int c1 = j ; int c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . Max ( Math . Max ( mat [ r1 c1 ] mat [ r1 c2 ]) Math . Max ( mat [ r2 c1 ] mat [ r2 c2 ])); } } return sum ; } // Driven Code public static void Main () { int [ ] mat = { { 112 42 83 119 } { 56 125 56 49 } { 15 78 101 43 } { 62 98 114 108 } }; Console . Write ( maxSum ( mat )); } } // This code is contributed // by ChitraNayal
PHP // PHP program to find maximum value // of top N/2 x N/2 matrix using row // and column reverse operations function maxSum ( $mat ) { $R = 4 ; $C = 4 ; $sum = 0 ; for ( $i = 0 ; $i < $R / 2 ; $i ++ ) for ( $j = 0 ; $j < $C / 2 ; $j ++ ) { $r1 = $i ; $r2 = $R - $i - 1 ; $c1 = $j ; $c2 = $C - $j - 1 ; // We can replace current cell [i j] // with 4 cells without changing // affecting other elements. $sum += max ( max ( $mat [ $r1 ][ $c1 ] $mat [ $r1 ][ $c2 ]) max ( $mat [ $r2 ][ $c1 ] $mat [ $r2 ][ $c2 ])); } return $sum ; } // Driver Code $mat = array ( array ( 112 42 83 119 ) array ( 56 125 56 49 ) array ( 15 78 101 43 ) array ( 62 98 114 108 )); echo maxSum ( $mat ) . ' n ' ; // This code is contributed // by Mukul Singh ?>
JavaScript < script > // Javascript program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations let R = 4 ; let C = 4 ; function maxSum ( mat ) { let sum = 0 ; for ( let i = 0 ; i < R / 2 ; i ++ ) { for ( let j = 0 ; j < C / 2 ; j ++ ) { let r1 = i ; let r2 = R - i - 1 ; let c1 = j ; let c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . max ( Math . max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) Math . max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])); } } return sum ; } // Driven Program let mat = [[ 112 42 83 119 ] [ 56 125 56 49 ] [ 15 78 101 43 ] [ 62 98 114 108 ]]; document . write ( maxSum ( mat )); // This code is contributed by avanitrachhadiya2155 < /script>
Lähtö
414
Aika monimutkaisuus: O(N 2 ).
Aputila: O(1) koska se käyttää vakiotilaa muuttujille
Luo tietokilpailu