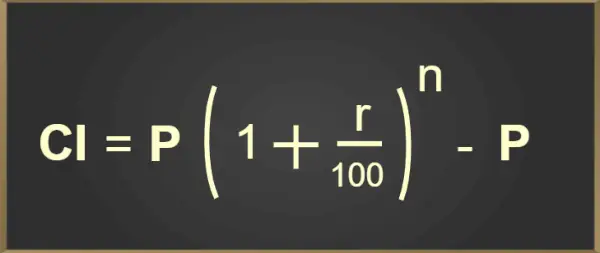
Korkokorko on laina- tai talletussummalle laskettava korko, jolle lasketaan korkoa pääomalle sekä aikaisemmille ansaitulle korolle.

Yleinen ero koron ja yksinkertaisen koron välillä on, että in korkoa korolle , korko lasketaan pääomalle sekä aiemmin ansaitun koron osalta, kun taas yksinkertainen korko riippuu vain sijoitetusta pääomasta.

Sisällysluettelo

• Mikä on korkokorko?
• Yhdistelmäkorkokaava
• Kuinka laskea korkokorko?
• Yhdistelmäkorkokaava – Johtaminen
• Puolen vuoden korkokaava
• Neljännesvuosittainen korkokaava
• Kuukauden korkokaava
• Päivittäinen korkokaava
• Jaksollinen yhdistelynopeuskaava
• Sääntö 72
• Peräkkäisten vuosien korkokorko
• Jatkuva korkokaava
• Joitakin muita yhdistelmiä kiinnostavia sovelluksia
• Koron ja yksinkertaisen koron välinen ero
• Esimerkkejä yhdistetyistä koroista
• Yhdistelmäkorko – harjoituskysymykset

Mikä on korkokorko?

Korkokorko on pääoman korkoa sekä pääomalle ansaittua korkoa. Sana yhdistelmäkorko koostuu kahdesta sanasta Yhdiste, joka tarkoittaa, että se koostuu kahdesta tai useammasta ja korko tarkoittaa summan lainaamisesta ansaittua rahaa. Näin ollen korkokorko on lainasta ansaittua rahaa, ja se koostuu kahdesta korosta, jotka ovat:

• Pääomasumman korko

• Pääomasummalle ansaitun koron korko jakson aikana

Yhdistetyn koron määritelmä

Korkoa korolle on pääomalle laskettu korko ja aiemmin ansaittu korko. Sitä merkitään C.I. Se on erittäin hyödyllinen sijoittamiseen ja lainan takaisinmaksuun. Se tunnetaan myös nimellä korkokorko.

Korkoa korolle on erittäin hyödyllinen pankki- ja rahoitussektoreilla ja on hyödyllinen myös muilla aloilla. Muutamia sen käyttötavoista ovat:

• Maan väestönkasvu
• Sijoituksen arvo tietyn ajanjakson aikana.
• Löytääksesi paisuneet kustannukset ja minkä tahansa tuotteen poistoarvon.
• Minkä tahansa laitoksen tai maan kasvun ennustamiseen.

Korkokorko (C.I) = Summa – Pääoma

Yhdistelmäkorkokaava

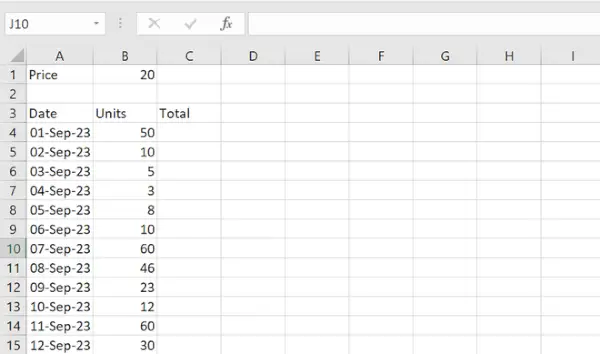
Korkoa korolle lasketaan sen jälkeen, kun kokonaissumma on laskettu tietyltä ajanjaksolta koron ja alkuperäisen pääoman perusteella. P:n alkupääomalle, vuosikoron r:lle, ajanjaksolle t vuosina, koron lisäyskertojen lukumäärälle vuosittain n, CI:n laskentakaava on seuraava:

CI = P(1 + r/100) ⁿ – P

Yllä oleva koron laskentakaava on lisätty alla olevaan kuvalomakkeeseen:

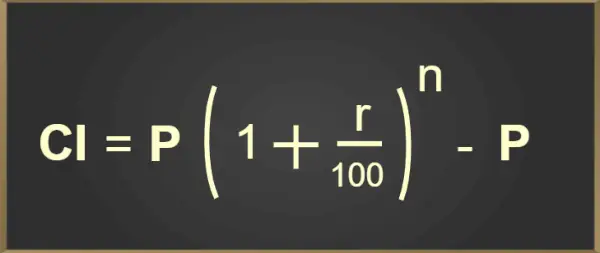
Yhdistelmäkorkokaava

Missä,

• P = Main
• r = Korko
• n = Kertojen lukumäärä, jolloin korko lasketaan vuodessa
• t = aika (vuosina)

Voimme kirjoittaa koron kaavan seuraavasti:

Korkokorko = A – P

Missä,

• A = Rahan kokonaismäärä yhdistämisen jälkeen
• P = Alkupääoma

Korkokorko = P(1 + r/n) ^nt -P

Missä,

• P = Alkupääoma
• r = vuosikorko
• n = Korkokertojen lukumäärä
• t = Vuosien lukumäärä

Korkokorko voidaan laskea vuosittain, puolivuosittain, neljännesvuosittain, kuukausittain, päivittäin jne. vaatimuksen mukaan.

Kuinka laskea korkokorko?

Korkoa korolle on sekä pääomalle että kertyneelle korolle maksettu korko. Jokaisella aikavälillä ansaittu korko lisätään alkuperäiseen pääomaan, joten pääoma nousee edelleen.

Käytä seuraavia menetelmiä löytääksesi koronkorot.

Vaihe 1: Huomautus, pääoma, korko ja ajanjakso annettu

Vaihe 2: Laske määrä kaavalla A = P(1 + r/100) ⁿ

Vaihe 3: Etsi korkokorko kaavalla CI = Summa – pääoma

Säännöllisin väliajoin tähän mennessä kertynyt korko lasketaan olemassa olevaan pääomaan ja sitten korko lasketaan laskettu uudelle päämiehelle . Uusi pääoma on yhtä suuri kuin alkupääoman ja tähän mennessä kertyneen koron summa.

Korkokorko = pääoman korko + pääoman korko (toisesta vuodesta eteenpäin)

Korkokorko lasketaan säännöllisin väliajoin, kuten vuosittain (vuosittain), puolivuosittain, neljännesvuosittain, kuukausittain, jne; Se on kuin sijoituksesta saatujen korkotulojen uudelleen sijoittaminen saa rahat kasvamaan nopeammin ajan myötä! Se on juuri sitä, mitä korkokorko tekee rahalle. Pankit tai mikä tahansa rahoituslaitos laskee summan vain koron perusteella.

Yhdistelmäkorkokaava – Johtaminen

Yhdistelmäkorkokaava on tehokas työkalu, jota käytetään rahoituksessa alkuperäisen pääoman ansaitun tai maksetun koron laskemiseen, joka sisältää sekä alkuperäisen pääoman että aikaisempien kausien aikana kertyneen koron. Koron koron kaava saadaan seuraavasti:

Missä,

• A on sijoituksen tai lainan tuleva arvo korkoineen
• P on pääomasumma (alkusijoitus tai lainasumma)
• r on vuosikorko (desimaalilukuna)
• n on kuinka monta kertaa korkoa korotetaan vuodessa
• t on aika, jolle rahaa sijoitetaan tai lainataan, vuosina

Yksinkertainen korkokaava

Yksinkertainen korko lasketaan vain pääoman määrälle. Se voidaan esittää kaavalla ,

Yhdistelmäkorkokaava jatkuvalla yhdistelyllä

Kun korkoa yhdistetään jatkuvasti (raamattoman monta kertaa vuodessa), koron kaava johdetaan käyttämällä jatkuvan koron kaavaa:

Missä,

• e on Eulerin luku (noin 2,71828)
• P on pääomasumma
• r on vuosikorko
• t on aika vuosissa

Yleinen yhdistetyn koron kaava

Yleisen koronkorkokaavan johtamiseksi harkitaan koron korkoa n kertaa vuodessa.

Jos P lisätään n kertaa vuodessa vuosikorolla r, korko r jaetaan n:llä ja sitä sovelletaan n kertaa vuodessa. Joten t vuoden kuluttua kaavasta tulee:

Missä,

• edustaa korkoa korkojaksoa kohti.
• nt on yhdistelmäjaksojen kokonaismäärä t vuoden aikana.

Tämä kaava havainnollistaa, kuinka alkuperäinen pääoma kasvaa ajan myötä, kun korkoa lisätään säännöllisin väliajoin . Kun n lähestyy ääretöntä (eli jatkuvaa sekoitusta), kaava konvergoi kohti jatkuvan sekoituksen kaavaa .

Yhteenvetona, koron kaava on seurausta jatkuvasta sekoituskaavasta, joka on mukautettu erillisiin sekoitusjaksoihin vuodessa. Se mahdollistaa sijoituksen tai lainan tulevan arvon laskemisen, huomioimalla säännöllisin väliajoin koronkorot.

Puolen vuoden korkokaava

Olkoon sijoitettu pääoma P ja korko R % vuodessa, joka lisätään puolivuosittain 't' vuoden ajan

Kuten se yhdistetään puolivuosittain, pääomaa muutetaan 6 kuukauden lopussa, ja siihen asti ansaitut korot lisätään pääomaan ja tästä tulee uusi pääoma. Vastaavasti lasketaan lopullinen summa.

Me tiedämme,

korko = R% vuodessa, laskettuna puolivuosittain

korko = (R/2) %

aika on t vuotta tiedämme, että t vuotta on 2t puoli vuotta.

Nyt,

A = P (1 + R/200) ^2t

CI = A – P

Neljännesvuosittainen korkokaava

Olkoon sijoitettu pääoma P ja korko R % vuodessa, joka yhdistetään neljännesvuosittain t vuoden ajalta.

Kuten se yhdistetään neljännesvuosittain, pääomaa muutetaan 3 kuukauden lopussa, ja siihen asti kertynyt korko lisätään pääomaan ja tästä tulee uusi pääoma. Vastaavasti lasketaan lopullinen summa.

me tiedämme,

korko = R % vuodessa yhdistettynä neljännesvuosittain

hinta = (R/4) %

aika on t vuotta tiedämme, että t vuotta on 4t neljännekset.

Nyt,

A = P(1 + R/400) ^4t

CI = A – P

Tarkistaa: Neljännesvuosittainen korkokaava

Kuukauden korkokaava

Jos korkoa korotetaan kuukausittain, korkokertojen määrä on 12 ja kuukausikorko on 1/12 vuotuisesta koronkorosta. Tästä syystä kuukausittainen yhdistetyn koron kaava annetaan muodossa

A = P[1 + (R/1200)] ^12t

CI = A – P

Tarkistaa: Kuukauden korkokaava

Päivittäinen korkokaava

Jos kiinnostus kasvaa päivittäin, niin.

Uusi korko on R/365 %

n = 365

Siksi päivittäinen yhdistetyn koron kaava annetaan seuraavasti:

A = P[1 + (R/36500)] ^365t

CI = A – P

Jaksollinen yhdistelynopeuskaava

Kokonaismäärä, mukaan lukien pääoma P ja korkokorko CI, saadaan seuraavasti:

A = P[1 + (r/n)] ^nt

missä,

• P = Main
• A = Lopullinen määrä
• r = vuosikorko
• n = Niiden kertojen lukumäärä, jolloin korko muodostuu
• t = aika (vuosina)

Näin ollen korkokorko on:

CI = A – P

Sääntö 72

Sääntö 72 on kaava, jolla arvioidaan, kuinka monen vuoden rahamme kaksinkertaistuvat, jos se yhdistetään vuosittain. varten esimerkki , jos rahamme sijoitetaan r % Lisätään vuosittain, niin kuluu 72/r vuotta ennen kuin rahamme tuplaantuu.

Tämä laskelma on hyödyllinen myös rahamme paisuneen arvon laskemiseen, eli se antaa kuinka monessa vuodessa omaisuutemme arvo puolittuu, jos se poistetaan vuosittain.

72 kaavan sääntö

Seuraavaa kaavaa käytetään arvioimaan vuosien lukumäärä, jolloin sijoituksemme kaksinkertaistuu.

N = 72/r

missä,

• N on arvioitu vuosiluku, jona rahamme tuplataan
• r on korko, jolla rahamme yhdistetään vuosittain

Esimerkki sääntö 72

Oletetaan, että Kabir on sijoittanut 10 00 000 rupiaa velkarahastoon, joka antaa 8 %:n tuoton. Selvitä, kuinka monessa vuodessa sen rahat kaksinkertaistuvat, jos ne yhdistetään vuosittain.

Käyttämällä yllä olevaa kaavaa: N = 72/8 = 9 vuotta

Täten, kestää 9 vuotta ennen kuin Kabirin rahat tuplaavat.

Peräkkäisten vuosien korkokorko

Jos meillä on sama summa ja sama korko. C.I. tietyn vuoden C.I on aina enemmän kuin edellisen vuoden C.I. (3. vuoden CI on suurempi kuin 2. vuoden CI). Kahden peräkkäisen vuoden CI:n välinen ero on yhden vuoden korko edellisen vuoden C.I:lle.

3. vuoden C.I – 2. vuoden C.I = 2. vuoden C.I × r × 1/100

Kahden peräkkäisen vuoden summien erotus on yhden vuoden korko edellisen vuoden summaan nähden.

3. vuoden määrä – 2. vuoden määrä = 2. vuoden määrä × r × 1/100

Tärkeimmät tulokset

Kun meillä on sama summa ja sama korko ,

C.I n:nnelle vuodelle = C.I (n – 1) vuodelle + yhden vuoden korko C.I:lle (n – 1) vuodelle

Jatkuva korkokaava

Jatkuvaa yhdistelykaavaa käytetään rahoituksessa laskemaan sellaisen sijoituksen lopullinen arvo, joka käy läpi jatkuvaa yhdistelyä eri ajanjaksojen aikana ja jonka arvoa lisätään ajan kuluessa. Jatkuvan sekoituksen kaava annetaan muodossa

Lopullinen arvo = nykyinen arvo × e ^rt

missä,

• r on korko
• t on aika

Lisätietoja, Jatkuva sekoituskaava

Joitakin muita yhdistelmiä kiinnostavia sovelluksia

Kasvu: Tätä käytetään pääasiassa kasvuun, jos toimialat liittyvät toisiinsa.

Tuotanto n vuoden jälkeen = alkuperäinen tuotanto × (1 + r/100) ⁿ

Poisto: Kun tuotteen hankintameno laskee r % vuodessa, niin sen arvo n vuoden kuluttua on

Nykyinen arvo × (1 + r/100) ⁿ

Väestöongelmat: Kun kaupungin, kaupungin tai kylän väkiluku kasvaa tietyllä nopeudella vuodessa.

Väestö n vuoden jälkeen = nykyinen väestö × (1 + r/100) ⁿ

Koron ja yksinkertaisen koron välinen ero

Yhdistetyn koron ja yksinkertaisen koron välinen ero voidaan oppia alla tässä artikkelissa

Yhdistelmäkorko vs yksinkertainen korko
Korkokorko (CI)	Simple Interest (SI)
CI on korkoa, joka lasketaan sekä pääomalle että aiemmin ansaitulle korolle.	SI on korko, joka lasketaan vain pääomalle.
Sama periaate, Rate ja Time period CI> KYLLÄ	Sama periaate, Rate ja Time period JOO
CI:n kaava on A = P(1 + R/100) T CI = A – P	SI:n kaava on JOS = (P×R×T) / 100

Esimerkkejä yhdistetyistä koroista

Joitakin esimerkkejä koron kaavoista ovat

Esimerkki 1: Etsi korkokorko, kun pääoma = Rs 6000, korko = 10 % vuodessa ja aika = 2 vuotta.

Ratkaisu:

Ensimmäisen vuoden korko = (6000 × 10 × 1)/100 = 600

Summa ensimmäisen vuoden lopussa = 6000 + 600 = 6600

Toisen vuoden korko = (6600 × 10 × 1) / 100 = 660

Summa toisen vuoden lopussa = 6600 + 660 = 7260

Korkokorko = 7260 – 6000 = 1260

Esimerkki 2: Mikä on 8000 Rs:n koronkorko kahden vuoden kuluttua, kun korko on 2 % vuodessa?

Ratkaisu:

Annettu,

• Pää P = 8000
• Korko r = 2 %
• Aika = 2 vuotta

kaavan mukaan

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100) ² = 8000 (102/100) ²

A = 8323

Korkokorko = A – P = 8323 – 8000 = 323 rupiaa

Esimerkki 3: Hari talletti Rs. 4000 rahoitusyhtiössä 2 vuoden korolla 5 % vuodessa. Mikä on korko, jonka Rohit saa 2 vuoden jälkeen?

Ratkaisu:

Annettu,

• Pää P = 4000
• Korko r = 5 %
• Aika = 2 vuotta

Kaavan mukaan,

A = P (1 + R/100) ⁿ

A = 4000 (1 + 5/100) ²

A = 4000 (105/100) ²

A = 4410

Korkokorko = A – P = 4410 – 4000 = 410

Esimerkki 4: Etsi Rs:n korkokorko. 2000 4 prosentin vuosikorolla 1,5 vuoden ajan. Milloin korko lasketaan puolivuosittain?

Ratkaisu:

Annettu,

• Pääp = 2000
• Korko r = 4 %
• Aika = 1,5 (eli 3 puoli vuotta)

kaavan mukaan,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Korkokorko = A – P = 2122 – 2000 = 122

Esimerkki 5: Mikä on koron 10 000 korko vuodeksi korolla 20 % vuodessa, jos korkoa korotetaan neljännesvuosittain?

Ratkaisu:

Annettu,

• Pääoma P = 10 000 Rs
• Korko R = 12 % (12/4 = 3 % vuosineljänneksessä)
• Aika = 1 vuosi (1 × 4 = 4 neljännestä)

Kaavan mukaan,

A = P (1 + R/100) ⁿ

A = 10 000 (1 + 3/100) ⁴

A = 10 000 (103/100) ⁴

A = 11255

Korkokorko = A – P = 11255 – 10000 = 1255

Esimerkki 6: Etsi korkokorko 5 % vuodessa 2 vuoden ajalta kyseiselle pääomalle, joka kahdessa vuodessa 5 % vuodessa tietyllä Rs. 400 yksinkertaista korkoa.

Ratkaisu:

Annettu,

• Yksinkertainen korko IF = 400
• Hinta R = 5 %
• Aika T = 2 vuotta

Kaavan mukaan,

Yksinkertainen korko = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 korkokorko = 5 %

P = 40 000/10 = 4 000 Rs

Aika = 2 vuotta

Kaavan mukaan,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Korkokorko = A – P = 4410 – 4000 = 410

Esimerkki 7: Etsi koron korko 30 000 Rs:lle 7 % korolla, joka korkoitetaan vuosittain kahden vuoden ajan.

Ratkaisu:

• Pääoma P = 30 000 Rs
• Hinta R = 7 %
• Aika = 2 vuotta

Kaavan mukaan,

A = P (1 + R/100) ⁿ

A = 30 000 (1 + 7/100) ²

A = 30 000 (107/100) ²

A = 34347

Korkokorko = A – P = 34347 – 30000 = 4347

Aiheeseen liittyvää luettavaa:

• Päivittäinen korkokorko
• Kuukauden korkokorko
• Luokan 8 yhdistetyn koron ratkaisu
• Yhdistelmäkorko – soveltuvuuskysymyksiä ja vastauksia
• Yksinkertainen kiinnostus

Yhdistelmäkorko – harjoituskysymykset

Erilaisia ​​korkokorkoja koskevia käytännön kysymyksiä ovat mm.

Q1. Selvitä summa, joka on maksettava 3 vuoden kuluttua, jos lainataan 10 000 summa 4% korolla, joka lisätään vuosittain.

Q2. Selvitä, että korko on maksettava 1,5 vuoden kuluttua, jos lainataan 2500 korkoa 6 % korolla puolivuosittain.

Q3. Laske korkokorko 9000 lainalle korolla 5 % neljännesvuosittain 15 kuukauden ajan.

Q4. Laske koronkorko 20 000 lainalle korolla 12 % 3 kuukaudeksi ja kuukausittain

Johtopäätös koronkorosta

Korkokorko on a tehokas rahoituskonsepti, jonka avulla sijoitukset tai lainat voivat kasvaa tai kertyä ajan myötä. Toisin kuin yksinkertainen korko, joka laskee koron vain alkuperäisestä pääomasta, korkoa korolle ottaa huomioon sekä alkuperäiselle pääomalle kertyneet korot että aiemmilta kausilta kertyneet korot.

Korkokorko - UKK

Mikä yhdistetyn intressin merkitys?

Korkokorko on pääomalle laskettu korko sekä aikaisemmalta kiinteältä ajalta ansaittu korko

Kuinka lasketaan korkokorko?

Korkokoron laskemiseksi lasketaan ensin lopullinen summa, jonka jälkeen se vähennetään pääomasta, jotta saadaan lopullinen korkokorko. Summa lasketaan kaavalla,

A = P(1 + R/100) ^t

CI = A – P

Onko yhdistetty korko parempi kuin yksinkertainen korko sijoittajille?

Kyllä, yhdistetty korko on sijoittajalle paljon parempi kuin yksinkertainen korko.

Mikä on yhdistetyn koron kaava, jos se yhdistetään päivittäin?

Oletetaan, että annettu pääoma on P, korko on R ja aikaväli on T vuotta, niin koron kaava, kun se yhdistetään päivittäin, on:

A = P(1 + R/365) ^{{365 × T}}

Mitä eroa on CI:n ja SI:n välillä?

Perusero CI:n ja SI:n välillä on, että SI on pääoman määrältä veloitettava korko, kun taas CI on pääoman määrältä veloitettava korko sekä pääomalle kertynyt korko