Ubicación óptima del punto para minimizar la distancia total

 #practiceLinkDiv { mostrar: ninguno !importante; }
#practiceLinkDiv { mostrar: ninguno !importante; } Dado un conjunto de puntos como y una línea como ax+by+c = 0. Necesitamos encontrar un punto en una línea dada para la cual la suma de distancias desde un conjunto de puntos dado sea mínima.
Ejemplo:

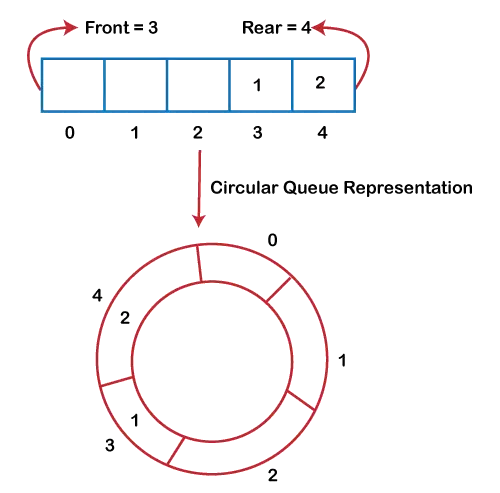
In above figure optimum location of point of x - y - 3 = 0 line is (2 -1) whose total distance with other points is 20.77 which is minimum obtainable total distance.Recommended Practice Ubicación óptima del punto para minimizar la distancia total ¡Pruébalo!
Si tomamos un punto en una línea dada a una distancia infinita, entonces el costo total de la distancia será infinito. Ahora, cuando movemos este punto en la línea hacia puntos dados, el costo total de la distancia comienza a disminuir y después de un tiempo comienza a aumentar nuevamente, lo que llega a infinito en el otro extremo infinito de la línea, por lo que la curva del costo de la distancia parece una curva en U y tenemos que encontrar el valor inferior de esta curva en U.
Como la curva en U no aumenta ni disminuye monótonamente, no podemos usar la búsqueda binaria para encontrar el punto más bajo. Aquí usaremos la búsqueda ternaria para encontrar el punto más bajo. La búsqueda ternaria omite un tercio del espacio de búsqueda en cada iteración. Puede leer más sobre la búsqueda ternaria. aquí .
Entonces, la solución procede de la siguiente manera: comenzamos con bajo y alto inicializados como algunos valores más pequeños y más grandes respectivamente, luego comenzamos la iteración en cada iteración, calculamos dos medios mid1 y mid2 que representan 1/3 y 2/3 de posición en el espacio de búsqueda, calculamos la distancia total de todos los puntos con mid1 y mid2 y actualizamos bajo o alto comparando estos costos de distancia. Esta iteración continúa hasta que bajo y alto se vuelven aproximadamente iguales.
C++ // C/C++ program to find optimum location and total cost #include using namespace std ; #define sq(x) ((x) * (x)) #define EPS 1e-6 #define N 5 // structure defining a point struct point { int x y ; point () {} point ( int x int y ) : x ( x ) y ( y ) { } }; // structure defining a line of ax + by + c = 0 form struct line { int a b c ; line ( int a int b int c ) : a ( a ) b ( b ) c ( c ) { } }; // method to get distance of point (x y) from point p double dist ( double x double y point p ) { return sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = -1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance double findOptimumCostUtil ( point p [] int n line l ) { double low = -1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x co-ordiantes // of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; // double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost double findOptimumCost ( int points [ N ][ 2 ] line l ) { point p [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver code to test above method int main () { line l ( 1 -1 -3 ); int points [ N ][ 2 ] = { { -3 -2 } { -1 0 } { -1 2 } { 1 2 } { 3 4 } }; cout < < findOptimumCost ( points l ) < < endl ; return 0 ; }
Java // A Java program to find optimum location // and total cost class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point static class point { int x y ; point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line of ax + by + c = 0 form static class line { int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of point (x y) from point p static double dist ( double x double y point p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ static double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ] ); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point p [] int n line l ) { double low = - 1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int points [][] line l ) { point [] p = new point [ N ] ; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ] ); return findOptimumCostUtil ( p N l ); } // Driver Code public static void main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int points [][] = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; System . out . println ( findOptimumCost ( points l )); } } // This code is contributed by Rajput-Ji
Python3 # A Python3 program to find optimum location # and total cost import math class Optimum_distance : # Class defining a point class Point : def __init__ ( self x y ): self . x = x self . y = y # Class defining a line of ax + by + c = 0 form class Line : def __init__ ( self a b c ): self . a = a self . b = b self . c = c # Method to get distance of point # (x y) from point p def dist ( self x y p ): return math . sqrt (( x - p . x ) ** 2 + ( y - p . y ) ** 2 ) # Utility method to compute total distance # all points when choose point on given # line has x-coordinate value as X def compute ( self p n l x ): res = 0 y = - 1 * ( l . a * x + l . c ) / l . b # Calculating Y of chosen point # by line equation for i in range ( n ): res += self . dist ( x y p [ i ]) return res # Utility method to find minimum total distance def find_Optimum_cost_untill ( self p n l ): low = - 1e6 high = 1e6 eps = 1e-6 + 1 # Loop until difference between low # and high become less than EPS while (( high - low ) > eps ): # mid1 and mid2 are representative x # co-ordiantes of search space mid1 = low + ( high - low ) / 3 mid2 = high - ( high - low ) / 3 dist1 = self . compute ( p n l mid1 ) dist2 = self . compute ( p n l mid2 ) # If mid2 point gives more total # distance skip third part if ( dist1 < dist2 ): high = mid2 # If mid1 point gives more total # distance skip first part else : low = mid1 # Compute optimum distance cost by # sending average of low and high as X return self . compute ( p n l ( low + high ) / 2 ) # Method to find optimum cost def find_Optimum_cost ( self p l ): n = len ( p ) p_arr = [ None ] * n # Converting 2D array input to point array for i in range ( n ): p_obj = self . Point ( p [ i ][ 0 ] p [ i ][ 1 ]) p_arr [ i ] = p_obj return self . find_Optimum_cost_untill ( p_arr n l ) # Driver Code if __name__ == '__main__' : obj = Optimum_distance () l = obj . Line ( 1 - 1 - 3 ) p = [ [ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ] ] print ( obj . find_Optimum_cost ( p l )) # This code is contributed by Sulu_mufi
C# // C# program to find optimum location // and total cost using System ; class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point public class point { public int x y ; public point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line // of ax + by + c = 0 form public class line { public int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of // point (x y) from point p static double dist ( double x double y point p ) { return Math . Sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance of all points when choose point on given line has x-coordinate value as X */ static double compute ( point [] p int n line l double X ) { double res = 0 ; // calculating Y of chosen point // by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point [] p int n line l ) { double low = - 1 e6 ; double high = 1 e6 ; // loop until difference between // low and high become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative // x co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by // sending average of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int [ ] points line l ) { point [] p = new point [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i 0 ] points [ i 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code public static void Main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int [ ] points = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; Console . WriteLine ( findOptimumCost ( points l )); } } // This code is contributed by 29AjayKumar
JavaScript < script > // A JavaScript program to find optimum location // and total cost function sq ( x ) { return x * x ; } let EPS = ( 1e-6 ) + 1 ; let N = 5 ; // structure defining a point class point { constructor ( x y ) { this . x = x ; this . y = y ; } } // structure defining a line of ax + by + c = 0 form class line { constructor ( a b c ) { this . a = a ; this . b = b ; this . c = c ; } } // method to get distance of point (x y) from point p function dist ( x y p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ function compute ( p n l X ) { let res = 0 ; // calculating Y of chosen point by line equation let Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( let i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance function findOptimumCostUtil ( p n l ) { let low = - 1e6 ; let high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space let mid1 = low + ( high - low ) / 3 ; let mid2 = high - ( high - low ) / 3 ; let dist1 = compute ( p n l mid1 ); let dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost function findOptimumCost ( points l ) { let p = new Array ( N ); // converting 2D array input to point array for ( let i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code let l = new line ( 1 - 1 - 3 ); let points = [[ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ]]; document . write ( findOptimumCost ( points l )); // This code is contributed by rag2127 < /script>
Producción
20.7652
Complejidad del tiempo: En 2 )
Espacio Auxiliar: En)