Este tutorial es una guía para principiantes para aprender estructuras de datos y algoritmos usando Python. En este artículo, analizaremos las estructuras de datos integradas, como listas, tuplas, diccionarios, etc., y algunas estructuras de datos definidas por el usuario, como listas enlazadas , árboles , graficos , etc., y algoritmos de recorrido, búsqueda y clasificación con la ayuda de ejemplos y preguntas de práctica buenos y bien explicados.

Liza

Listas de Python Son colecciones ordenadas de datos al igual que las matrices en otros lenguajes de programación. Permite diferentes tipos de elementos en la lista. La implementación de Python List es similar a Vectors en C++ o ArrayList en JAVA. La operación costosa es insertar o eliminar el elemento desde el principio de la Lista, ya que es necesario desplazar todos los elementos. La inserción y eliminación al final de la lista también puede resultar costosa en el caso de que la memoria preasignada se llene.

Ejemplo: creación de una lista de Python

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Se puede acceder a los elementos de la lista mediante el índice asignado. En el índice inicial de Python de la lista, una secuencia es 0 y el índice final es (si hay N elementos) N-1.

Ejemplo: operaciones de lista de Python

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

tupla

tuplas de pitón son similares a las listas pero las tuplas son inmutable en la naturaleza, es decir, una vez creado no se puede modificar. Al igual que una Lista, una Tupla también puede contener elementos de varios tipos.

En Python, las tuplas se crean colocando una secuencia de valores separados por 'comas' con o sin el uso de paréntesis para agrupar la secuencia de datos.

Nota: Para crear una tupla de un elemento debe haber una coma al final. Por ejemplo, (8,) creará una tupla que contiene 8 como elemento.

Ejemplo: operaciones de tuplas de Python

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Colocar

conjunto de pitón es una colección mutable de datos que no permite ninguna duplicación. Los conjuntos se utilizan básicamente para incluir pruebas de membresía y eliminar entradas duplicadas. La estructura de datos utilizada en esto es Hashing, una técnica popular para realizar inserción, eliminación y recorrido en O(1) en promedio.

Si hay varios valores presentes en la misma posición de índice, entonces el valor se agrega a esa posición de índice para formar una lista vinculada. En CPython Sets se implementan utilizando un diccionario con variables ficticias, donde las claves son los miembros establecidos con mayores optimizaciones para la complejidad del tiempo.

Establecer implementación:

Conjuntos con numerosas operaciones en una sola HashTable:

Ejemplo: operaciones de conjuntos de Python

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Conjuntos congelados

Conjuntos congelados En Python hay objetos inmutables que solo admiten métodos y operadores que producen un resultado sin afectar el conjunto o conjuntos congelados a los que se aplican. Si bien los elementos de un conjunto se pueden modificar en cualquier momento, los elementos del conjunto congelado permanecen iguales después de la creación.

Ejemplo: conjunto congelado de Python

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Cadena

Cadenas de Python es la matriz inmutable de bytes que representan caracteres Unicode. Python no tiene un tipo de datos de carácter, un solo carácter es simplemente una cadena con una longitud de 1.

Nota: Como las cadenas son inmutables, modificar una cadena dará como resultado la creación de una nueva copia.

Ejemplo: operaciones de cadenas de Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Diccionario

diccionario de pitón es una colección desordenada de datos que almacena datos en el formato de par clave:valor. Es como las tablas hash en cualquier otro lenguaje con la complejidad temporal de O(1). La indexación del Diccionario Python se realiza con la ayuda de claves. Estos son de cualquier tipo hash, es decir, un objeto que nunca puede cambiar, como cadenas, números, tuplas, etc. Podemos crear un diccionario usando llaves ({}) o comprensión de diccionario.

Ejemplo: operaciones del diccionario Python

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matriz

Una matriz es una matriz 2D donde cada elemento tiene estrictamente el mismo tamaño. Para crear una matriz usaremos el Paquete numérico .

Ejemplo: operaciones matriciales de Python NumPy

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Producción

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

matriz de bytes

Python Bytearray proporciona una secuencia mutable de números enteros en el rango 0 <= x < 256.

Ejemplo: operaciones de Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Lista enlazada

A lista enlazada Es una estructura de datos lineal, en la que los elementos no se almacenan en ubicaciones de memoria contiguas. Los elementos de una lista vinculada están vinculados mediante punteros como se muestra en la siguiente imagen:

Una lista vinculada está representada por un puntero al primer nodo de la lista vinculada. El primer nodo se llama cabeza. Si la lista vinculada está vacía, entonces el valor del encabezado es NULL. Cada nodo de una lista consta de al menos dos partes:

• Datos
• Puntero (o referencia) al siguiente nodo

Ejemplo: definición de lista enlazada en Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Creemos una lista enlazada simple con 3 nodos.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nulo | | 3 | nulo |  +----+------+ +----+------+ +----+------+ ''' segundo.siguiente = tercero ; # Vincular el segundo nodo con el tercer nodo ''' Ahora el siguiente del segundo nodo se refiere al tercero. Entonces los tres nodos están vinculados.  llist.head segundo tercio | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | nulo |  +----+------+ +----+------+ +----+------+ ''' 

Recorrido de lista enlazada

En el programa anterior, creamos una lista enlazada simple con tres nodos. Recorramos la lista creada e imprimamos los datos de cada nodo. Para el recorrido, escribamos una función de propósito general printList() que imprima cualquier lista dada.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Más artículos sobre lista enlazada

• Inserción de lista enlazada
• Eliminación de lista vinculada (eliminación de una clave determinada)
• Eliminación de lista vinculada (eliminación de una clave en una posición determinada)
• Encontrar la longitud de una lista enlazada (iterativa y recursiva)
• Buscar un elemento en una lista enlazada (iterativa y recursiva)
• Enésimo nodo desde el final de una lista vinculada
• Invertir una lista enlazada

A pila es una estructura de datos lineal que almacena elementos en forma de último en entrar/primero en salir (LIFO) o primero en entrar/último en salir (FILO). En la pila, se agrega un nuevo elemento en un extremo y se elimina un elemento solo de ese extremo. Las operaciones de inserción y eliminación a menudo se denominan push y pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Como pila, el cola es una estructura de datos lineal que almacena elementos según el principio Primero en entrar, primero en salir (FIFO). En una cola, el elemento agregado menos recientemente se elimina primero. Un buen ejemplo de cola es cualquier cola de consumidores de un recurso en la que el consumidor que llegó primero recibe el servicio primero.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Colas prioritarias son estructuras de datos abstractas donde cada dato/valor en la cola tiene una cierta prioridad. Por ejemplo, en las aerolíneas el equipaje con el título Business o First-class llega antes que el resto. Priority Queue es una extensión de la cola con las siguientes propiedades.

• Un elemento con alta prioridad se retira de la cola antes que un elemento con baja prioridad.
• Si dos elementos tienen la misma prioridad, se sirven según su orden en la cola.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] devuelve elemento excepto IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) mientras no sea myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Montón

módulo heapq en Python proporciona la estructura de datos del montón que se utiliza principalmente para representar una cola de prioridad. La propiedad de esta estructura de datos es que siempre proporciona el elemento más pequeño (montón mínimo) cada vez que se extrae el elemento. Cada vez que se empujan o sacan elementos, se mantiene la estructura del montón. El elemento heap[0] también devuelve el elemento más pequeño cada vez. Admite la extracción e inserción del elemento más pequeño en tiempos O (log n).

Generalmente, los Heaps pueden ser de dos tipos:

• Montón máximo: En un Max-Heap, la clave presente en el nodo raíz debe ser la mayor entre las claves presentes en todos sus hijos. La misma propiedad debe ser verdadera de forma recursiva para todos los subárboles de ese árbol binario.
• Montón mínimo: En un Min-Heap, la clave presente en el nodo raíz debe ser la mínima entre las claves presentes en todos sus hijos. La misma propiedad debe ser verdadera de forma recursiva para todos los subárboles de ese árbol binario.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Más artículos sobre montón

• montón binario
• K'th elemento más grande en una matriz
• K'th elemento más pequeño/más grande en una matriz sin clasificar
• Ordenar una matriz casi ordenada
• K-ésimo subconjunto contiguo de suma más grande
• Suma mínima de dos números formados a partir de dígitos de una matriz

Un árbol es una estructura de datos jerárquica que se parece a la siguiente figura:

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

El nodo superior del árbol se llama raíz, mientras que los nodos inferiores o los nodos sin hijos se denominan nodos hoja. Los nodos que están directamente debajo de un nodo se llaman hijos y los nodos que están directamente encima de algo se llaman padres.

A árbol binario es un árbol cuyos elementos pueden tener casi dos hijos. Dado que cada elemento de un árbol binario puede tener sólo 2 hijos, normalmente los llamamos hijos izquierdo y derecho. Un nodo de árbol binario contiene las siguientes partes.

• Datos
• Puntero al niño izquierdo
• Puntero al niño correcto

Ejemplo: definición de clase de nodo

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Ahora creemos un árbol con 4 nodos en Python. Supongamos que la estructura del árbol se ve como se muestra a continuación:

 tree  ----  1  <-- root  /   2 3   /  4 

Ejemplo: agregar datos al árbol

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Recorrido del árbol

Los árboles se pueden atravesar. En maneras diferentes. A continuación se detallan las formas generalmente utilizadas para atravesar árboles. Consideremos el siguiente árbol:

 tree  ----  1  <-- root  /   2 3   /  4 5 

Primeros recorridos en profundidad:

• En orden (izquierda, raíz, derecha): 4 2 5 1 3
• Reserva (raíz, izquierda, derecha): 1 2 4 5 3
• Orden posterior (izquierda, derecha, raíz): 4 5 2 3 1

Orden del algoritmo (árbol)

• Atraviese el subárbol izquierdo, es decir, llame a Inorder(subárbol izquierdo)
• Visita la raíz.
• Atraviese el subárbol derecho, es decir, llame a Inorder(subárbol derecho)

Reserva de algoritmo (árbol)

• Visita la raíz.
• Atraviese el subárbol izquierdo, es decir, llame a Preorden (subárbol izquierdo)
• Atraviese el subárbol derecho, es decir, llame a Preorder(subárbol derecho)

Algoritmo Giro postal(árbol)

• Atraviese el subárbol izquierdo, es decir, llame a Postorder(subárbol izquierdo)
• Atraviese el subárbol derecho, es decir, llame a Postorder(subárbol derecho)
• Visita la raíz.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Complejidad del tiempo: O (n)

Recorrido de orden de nivel o amplitud primero

recorrido de orden de nivel de un árbol es el recorrido en anchura del árbol. El recorrido de orden de nivel del árbol anterior es 1 2 3 4 5.

Para cada nodo, primero se visita el nodo y luego sus nodos secundarios se colocan en una cola FIFO. A continuación se muestra el algoritmo para el mismo:

• Crear una cola vacía q
• temp_node = raíz /*comenzar desde la raíz*/
• Bucle mientras temp_node no sea NULL
  • imprimir temp_node->datos.
  • Ponga en cola los hijos de temp_node (primero los hijos de la izquierda y luego los de la derecha) en q
  • Quitar de la cola un nodo de q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Imprimir el frente de la cola y # eliminarlo de la cola print (queue[0].data) node = queue.pop(0) # Poner en cola al hijo izquierdo si node.left no es Ninguno: queue.append(node.left ) # Poner en cola el hijo derecho si node.right no es Ninguno: queue.append(node.right) # Programa controlador para probar la función anterior root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Nodo(4) root.left.right = Nodo(5) print ('El recorrido del orden de niveles del árbol binario es -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Complejidad del tiempo: O(n)

Más artículos sobre árbol binario

• Inserción en un árbol binario
• Eliminación en un árbol binario
• Recorrido de árbol en orden sin recursividad
• ¡Inorder Tree Traversal sin recursividad y sin pila!
• Imprimir recorrido posterior al pedido a partir de recorridos en orden y preorden dados
• Encuentre el recorrido posterior al pedido de BST desde el recorrido previo al pedido

Árbol de búsqueda binaria es una estructura de datos de árbol binario basada en nodos que tiene las siguientes propiedades:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A grafico Es una estructura de datos no lineal que consta de nodos y aristas. A los nodos a veces también se les llama vértices y los bordes son líneas o arcos que conectan dos nodos cualesquiera en el gráfico. Más formalmente, un gráfico se puede definir como un gráfico que consta de un conjunto finito de vértices (o nodos) y un conjunto de aristas que conectan un par de nodos.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Programa controlador para la clase gráfica anterior si __name__ == '__main__' : V = 5 gráfico = Gráfico(V) gráfico.add_edge(0, 1) gráfico.add_edge(0, 4) gráfico.add_edge(1, 2) gráfico.add_edge(1, 3) gráfico.add_edge(1, 4) gráfico.add_edge(2, 3) gráfico.add_edge(3, 4) gráfico.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Lista de adyacencia de la cabeza del vértice 1 -> 4 -> 3 -> 2 -> 0 Lista de adyacencia de la cabeza del vértice 2 -> 3 -> 1 Lista de adyacencia de la cabeza del vértice 3 -> 4 -> 2 -> 1 Adyacencia lista de vértice 4 cabeza -> 3 -> 1 -> 0 

Recorrido primero en amplitud porque un gráfico es similar al recorrido primero en amplitud de un árbol. El único inconveniente aquí es que, a diferencia de los árboles, los gráficos pueden contener ciclos, por lo que podemos llegar al mismo nodo nuevamente. Para evitar procesar un nodo más de una vez, utilizamos una matriz booleana visitada. Por simplicidad, se supone que todos los vértices son accesibles desde el vértice inicial.

Por ejemplo, en el siguiente gráfico, comenzamos a recorrer desde el vértice 2. Cuando llegamos al vértice 0, buscamos todos los vértices adyacentes. 2 también es un vértice adyacente a 0. Si no marcamos los vértices visitados, entonces 2 se procesará nuevamente y se convertirá en un proceso sin finalización. Un recorrido en amplitud primero del siguiente gráfico es 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Complejidad del tiempo: O (V + E) donde V es el número de vértices del gráfico y E es el número de aristas del gráfico.

Primera búsqueda en profundidad o DFS

Primer recorrido en profundidad porque un gráfico es similar al primer recorrido en profundidad de un árbol. El único inconveniente aquí es que, a diferencia de los árboles, los gráficos pueden contener ciclos y un nodo puede visitarse dos veces. Para evitar procesar un nodo más de una vez, utilice una matriz booleana visitada.

Algoritmo:

• Cree una función recursiva que tome el índice del nodo y una matriz visitada.
• Marque el nodo actual como visitado e imprima el nodo.
• Recorra todos los nodos adyacentes y no marcados y llame a la función recursiva con el índice del nodo adyacente.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 

Following is DFS from (starting from vertex 2) 2 0 1 3 

Más artículos sobre gráfico

• Representaciones gráficas usando set y hash
• Encuentra el vértice madre en un gráfico
• Primera búsqueda iterativa en profundidad
• Cuente el número de nodos en un nivel determinado en un árbol usando BFS
• Cuente todos los caminos posibles entre dos vértices.

El proceso en el que una función se llama a sí misma directa o indirectamente se llama recursividad y la función correspondiente se llama función recursiva . Utilizando algoritmos recursivos, ciertos problemas se pueden resolver con bastante facilidad. Ejemplos de tales problemas son las Torres de Hanoi (TOH), los recorridos de árboles en orden/preorden/postorder, DFS de Graph, etc.

def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 

3 2 1 1 2 3 

• recursividad
• Recursividad en Python
• Preguntas de práctica para la recursividad | Serie 1
• Preguntas de práctica para la recursividad | Conjunto 2
• Preguntas de práctica para la recursividad | Conjunto 3
• Preguntas de práctica para la recursividad | Conjunto 4
• Preguntas de práctica para la recursividad | Conjunto 5
• Preguntas de práctica para la recursividad | Conjunto 6
• Preguntas de práctica para la recursividad | Conjunto 7

>>> Más

Programación dinámica

Programación dinámica Es principalmente una optimización sobre la simple recursividad. Siempre que veamos una solución recursiva que tenga llamadas repetidas para las mismas entradas, podemos optimizarla usando la Programación Dinámica. La idea es simplemente almacenar los resultados de los subproblemas, de modo que no tengamos que volver a calcularlos cuando sea necesario más adelante. Esta simple optimización reduce las complejidades temporales de exponencial a polinómica. Por ejemplo, si escribimos una solución recursiva simple para los números de Fibonacci, obtenemos una complejidad temporal exponencial y si la optimizamos almacenando soluciones de subproblemas, la complejidad temporal se reduce a lineal.

Tabulación versus memorización

Hay dos formas diferentes de almacenar los valores para que se puedan reutilizar los valores de un subproblema. Aquí, discutiremos dos patrones para resolver problemas de programación dinámica (DP):

• Tabulación: De abajo hacia arriba
• Memorización: De arriba hacia abajo

Tabulación

Como sugiere el propio nombre, comenzando desde abajo y acumulando respuestas hasta arriba. Discutamos en términos de transición estatal.

Describamos un estado para nuestro problema DP como dp[x] con dp[0] como estado base y dp[n] como nuestro estado de destino. Entonces, necesitamos encontrar el valor del estado de destino, es decir, dp[n].

Si comenzamos nuestra transición desde nuestro estado base, es decir, dp[0] y seguimos nuestra relación de transición de estado para alcanzar nuestro estado de destino dp[n], lo llamamos enfoque de abajo hacia arriba, ya que está bastante claro que comenzamos nuestra transición desde el estado base inferior y alcanzó el estado deseado superior.

Ahora bien, ¿por qué lo llamamos método de tabulación?

Para saber esto, primero escribamos un código para calcular el factorial de un número utilizando el enfoque ascendente. Una vez más, como nuestro procedimiento general para resolver un DP, primero definimos un estado. En este caso, definimos un estado como dp[x], donde dp[x] es para encontrar el factorial de x.

Ahora bien, es bastante obvio que dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 

Memorización

Una vez más, describámoslo en términos de transición estatal. Si necesitamos encontrar el valor para algún estado, digamos dp[n] y en lugar de comenzar desde el estado base, es decir, dp[0], pedimos nuestra respuesta a los estados que pueden alcanzar el estado de destino dp[n] después de la transición de estado. relación, entonces es la moda de arriba hacia abajo de DP.

Aquí, comenzamos nuestro viaje desde el estado de destino más alto y calculamos su respuesta teniendo en cuenta los valores de los estados que pueden alcanzar el estado de destino, hasta llegar al estado base más bajo.

Una vez más, escribamos el código para el problema factorial de arriba hacia abajo.

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 

Más artículos sobre programación dinámica

• Propiedad óptima de la subestructura
• Propiedad de subproblemas superpuestos
• Números de Fibonacci
• Subconjunto con suma divisible por m
• Subsecuencia creciente de suma máxima
• Subcadena común más larga

>>> Más

Algoritmos de búsqueda

Búsqueda lineal

• Comience desde el elemento más a la izquierda de arr[] y uno por uno compare x con cada elemento de arr[]
• Si x coincide con un elemento, devuelve el índice.
• Si x no coincide con ninguno de los elementos, devuelve -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 

Element is present at index 3 

La complejidad temporal del algoritmo anterior es O (n).

Para obtener más información, consulte Búsqueda lineal .

Búsqueda binaria

Busque una matriz ordenada dividiendo repetidamente el intervalo de búsqueda por la mitad. Comience con un intervalo que cubra toda la matriz. Si el valor de la clave de búsqueda es menor que el elemento en el medio del intervalo, reduzca el intervalo a la mitad inferior. De lo contrario, limítelo a la mitad superior. Verifique repetidamente hasta que se encuentre el valor o el intervalo esté vacío.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Si el elemento está presente en el medio if arr[mid] == x: return mid # Si el elemento es más pequeño que mid, entonces # solo puede estar presente en el subarreglo izquierdo elif arr[mid]> x: return binarioSearch(arr, l, mid-1, x) # De lo contrario, el elemento solo puede estar presente # en el subarreglo derecho else: devuelve binarioSearch(arr, mid + 1, r, x ) else: # El elemento no está presente en la matriz return -1 # Código del controlador arr = [ 2, 3, 4, 10, 40 ] x = 10 # Resultado de la llamada a la función = binarioSearch(arr, 0, len(arr)-1 , x) si resultado != -1: imprimir ('El elemento está presente en el índice % d' % resultado) else: imprimir ('El elemento no está presente en la matriz') 

Element is present at index 3 

La complejidad temporal del algoritmo anterior es O (log (n)).

Para obtener más información, consulte Búsqueda binaria .

Algoritmos de clasificación

Orden de selección

El clasificación de selección El algoritmo ordena una matriz encontrando repetidamente el elemento mínimo (considerando el orden ascendente) de la parte no ordenada y colocándolo al principio. En cada iteración de ordenación por selección, el elemento mínimo (considerando el orden ascendente) del subarreglo sin ordenar se selecciona y se mueve al subarreglo ordenado.

Diagrama de flujo del tipo de selección:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Intercambia el elemento mínimo encontrado con # el primer elemento A[i], A[min_idx] = A[min_idx], A[i] # Código del controlador para probar arriba print ('Matriz ordenada ') para i en el rango(len(A)): print('%d' %A[i]), 

Sorted array 11 12 22 25 64 

Complejidad del tiempo: En ² ) ya que hay dos bucles anidados.

Espacio Auxiliar: O(1)

Ordenamiento de burbuja

Ordenamiento de burbuja es el algoritmo de clasificación más simple que funciona intercambiando repetidamente los elementos adyacentes si están en el orden incorrecto.

Ilustración:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Código de controlador para probar arriba arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('La matriz ordenada es:') for i in range(len(arr)): print ('%d' %arr[i]), 

Sorted array is: 11 12 22 25 34 64 90 

Complejidad del tiempo: En ² )

Tipo de inserción

Para ordenar una matriz de tamaño n en orden ascendente usando tipo de inserción :

• Itere desde arr[1] hasta arr[n] sobre la matriz.
• Compare el elemento actual (clave) con su predecesor.
• Si el elemento clave es más pequeño que su predecesor, compárelo con los elementos anteriores. Mueva los elementos más grandes una posición hacia arriba para dejar espacio para el elemento intercambiado.

Ilustración:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 y clave < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 

 5 6 11 12 13 

Complejidad del tiempo: En ² ))

Combinar ordenar

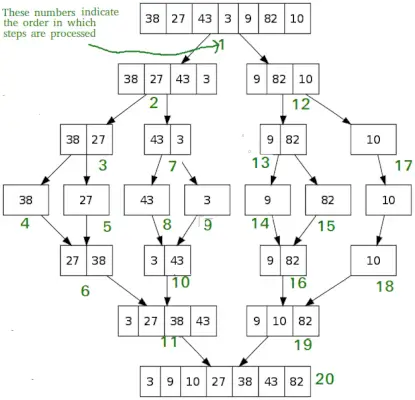
Al igual que la clasificación rápida, Combinar ordenar es un algoritmo divide y vencerás. Divide la matriz de entrada en dos mitades, se llama a sí mismo para las dos mitades y luego fusiona las dos mitades ordenadas. La función merge() se utiliza para fusionar dos mitades. La combinación (arr, l, m, r) es un proceso clave que supone que arr[l..m] y arr[m+1..r] están ordenados y fusiona los dos subarreglos ordenados en uno.

MergeSort(arr[], l, r) If r>l 1. Encuentre el punto medio para dividir la matriz en dos mitades: medio m = l+ (r-l)/2 2. Llame a mergeSort para la primera mitad: Llame a mergeSort(arr, l, m) 3. Llame a mergeSort para la segunda mitad: Llame mergeSort(arr, m+1, r) 4. Fusionar las dos mitades ordenadas en los pasos 2 y 3: llame a merge(arr, l, m, r) 

# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Encontrar la mitad de la matriz mid = len(arr)//2 # Dividir los elementos de la matriz L = arr[:mid] # en 2 mitades R = arr[mid:] # Ordenar la primera mitad mergeSort(L) # Ordenar la segunda mitad mergeSort(R) i = j = k = 0 # Copiar datos a las matrices temporales L[] y R[] mientras i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 

Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 

Complejidad del tiempo: O(n(iniciar sesión))

Ordenación rápida

Como fusionar orden, Ordenación rápida es un algoritmo divide y vencerás. Elige un elemento como pivote y divide la matriz dada alrededor del pivote seleccionado. Hay muchas versiones diferentes de QuickSort que seleccionan el pivote de diferentes maneras.

Elija siempre el primer elemento como pivote.

• Elija siempre el último elemento como pivote (implementado a continuación)
• Elija un elemento aleatorio como pivote.
• Elija la mediana como pivote.

El proceso clave en QuickSort es la partición(). El objetivo de las particiones es, dada una matriz y un elemento x de la matriz como pivote, colocar x en su posición correcta en la matriz ordenada y colocar todos los elementos más pequeños (menores que x) antes de x, y colocar todos los elementos mayores (mayores que x) después X. Todo esto debe hacerse en tiempo lineal.

/* low -->Índice inicial, alto --> Índice final */ quickSort(arr[], bajo, alto) { if (low { /* pi es el índice de partición, arr[pi] ahora está en el lugar correcto */ pi = partición(arr, bajo, alto); QuickSort(arr, bajo, pi - 1); // Antes de pi QuickSort(arr, pi + 1, alto); // Después de pi } } 

Algoritmo de partición

Puede haber muchas maneras de hacer la partición, siguiendo pseudocódigo Adopta el método dado en el libro CLRS. La lógica es simple, comenzamos desde el elemento más a la izquierda y realizamos un seguimiento del índice de elementos más pequeños (o iguales) como i. Mientras recorremos, si encontramos un elemento más pequeño, intercambiamos el elemento actual con arr[i]. De lo contrario ignoramos el elemento actual.

/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j  <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) } 

# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start  < end: # Increment the start pointer till it finds an # element greater than pivot while start  < len(array) and array[start]  <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivote: fin -= 1 # Si el inicio y el final no se han cruzado, # intercambie los números al inicio y al final if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 

Sorted array: [1, 5, 7, 8, 9, 10] 

Complejidad del tiempo: O(n(iniciar sesión))

Ordenar concha

Ordenar concha es principalmente una variación de la ordenación por inserción. En la ordenación por inserción, movemos los elementos solo una posición hacia adelante. Cuando es necesario mover un elemento mucho más adelante, intervienen muchos movimientos. La idea de shellSort es permitir el intercambio de elementos lejanos. En shellSort, ordenamos la matriz h para un valor grande de h. Seguimos reduciendo el valor de h hasta que se convierte en 1. Se dice que una matriz está ordenada en h si todas las sublistas de cada h ^th El elemento está ordenado.

# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = espacio # verifique la matriz de izquierda a derecha # hasta el último índice posible de j mientras j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # ahora, miramos hacia atrás desde el índice i hacia la izquierda # intercambiamos los valores que no están en el orden correcto. k = i mientras k - espacio> -1: si arr[k - espacio]> arr[k]: arr[k-espacio],arr[k] = arr[k],arr[k-espacio] k -= 1 espacio //= 2 # controlador para verificar el código arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) 

input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 

Complejidad del tiempo: En ² ).