Las limitaciones de los árboles de búsqueda binarios tradicionales pueden resultar frustrantes. Conozca B-Tree, la estructura de datos con múltiples talentos que puede manejar cantidades masivas de datos con facilidad. Cuando se trata de almacenar y buscar grandes cantidades de datos, los árboles de búsqueda binarios tradicionales pueden resultar poco prácticos debido a su bajo rendimiento y alto uso de memoria. Los B-Trees, también conocidos como B-Tree o Balanced Tree, son un tipo de árbol autoequilibrado que fue diseñado específicamente para superar estas limitaciones.

A diferencia de los árboles de búsqueda binarios tradicionales, los B-Trees se caracterizan por la gran cantidad de claves que pueden almacenar en un único nodo, por lo que también se les conoce como árboles de claves grandes. Cada nodo en un árbol B puede contener múltiples claves, lo que permite que el árbol tenga un factor de ramificación mayor y, por lo tanto, una altura menor. Esta altura reducida genera menos E/S de disco, lo que resulta en operaciones de búsqueda e inserción más rápidas. Los B-Trees son particularmente adecuados para sistemas de almacenamiento que tienen un acceso a datos lento y voluminoso, como discos duros, memorias flash y CD-ROM.

B-Trees mantiene el equilibrio asegurando que cada nodo tenga un número mínimo de claves, por lo que el árbol siempre está equilibrado. Este equilibrio garantiza que la complejidad temporal de operaciones como inserción, eliminación y búsqueda sea siempre O (log n), independientemente de la forma inicial del árbol.

Complejidad temporal del árbol B:

Sr. No.	Algoritmo	Complejidad del tiempo
1.	Buscar	O(log n)
2.	Insertar	O(log n)
3.	Borrar	O(log n)

Nota: n es el número total de elementos en el árbol B

Propiedades del árbol B:

• Todas las hojas están al mismo nivel.
• B-Tree se define mediante el término grado mínimo ' t '. El valor de ' t 'depende del tamaño del bloque de disco.
• Cada nodo, excepto la raíz, debe contener al menos claves t-1. La raíz puede contener un mínimo de 1 llave.
• Todos los nodos (incluida la raíz) pueden contener como máximo ( 2*t – 1 ) llaves.
• El número de hijos de un nodo es igual al número de claves que contiene más 1 .
• Todas las claves de un nodo se ordenan en orden creciente. El niño entre dos llaves k1 y k2 contiene todas las claves en el rango de k1 y k2 .
• B-Tree crece y se reduce desde la raíz, a diferencia del árbol de búsqueda binaria. Los árboles de búsqueda binaria crecen hacia abajo y también se encogen desde abajo.
• Al igual que otros árboles de búsqueda binaria equilibrados, la complejidad temporal para buscar, insertar y eliminar es O (log n).
• La inserción de un nodo en el árbol B ocurre solo en el nodo hoja.

A continuación se muestra un ejemplo de un árbol B de orden mínimo 5.
Nota: que en la práctica B-Trees, el valor del pedido mínimo es mucho más que 5.

Podemos ver en el diagrama anterior que todos los nodos hoja están en el mismo nivel y todos los no hojas no tienen un subárbol vacío y tienen una clave menos que el número de sus hijos.

Datos interesantes sobre los árboles B:

• La altura mínima del B-Tree que puede existir con n número de nodos y m es el número máximo de hijos que puede tener un nodo es:
• La altura máxima del B-Tree que puede existir con n número de nodos y t es el número mínimo de hijos que puede tener un nodo no raíz es: y

Recorrido en árbol B:

El recorrido también es similar al recorrido en orden del árbol binario. Comenzamos desde el hijo más a la izquierda, imprimimos recursivamente el hijo más a la izquierda y luego repetimos el mismo proceso para los hijos y las claves restantes. Al final, imprima recursivamente el hijo más a la derecha.

Operación de búsqueda en B-Tree:

La búsqueda es similar a la búsqueda en el árbol de búsqueda binaria. Sea la clave a buscar k.

• Comience desde la raíz y recorra recursivamente hacia abajo.
• Por cada nodo no hoja visitado,
  • Si el nodo tiene la clave, simplemente devolvemos el nodo.
  • De lo contrario, recurriremos al hijo apropiado (el hijo que está justo antes de la primera clave mayor) del nodo.
• Si llegamos a un nodo hoja y no encontramos k en el nodo hoja, devolvemos NULL.

Buscar en un árbol B es similar a buscar en un árbol binario. El algoritmo es similar y va con recursividad. En cada nivel, la búsqueda se optimiza como si el valor clave no estuviera presente en el rango del padre, entonces la clave estaría presente en otra rama. Como estos valores limitan la búsqueda, también se les conoce como valores límite o valores de separación. Si llegamos a un nodo hoja y no encontramos la clave deseada, se mostrará NULL.

Algoritmo para buscar un elemento en un árbol B: –

C++

struct> Node {> > int> n;> > int> key[MAX_KEYS];> > Node* child[MAX_CHILDREN];> > bool> leaf;> };> Node* BtreeSearch(Node* x,> int> k) {> > int> i = 0;> > while> (i n && k>x->tecla[i]) {> > i++;> > }> > if> (i n && k == x->clave[i]) {> > return> x;> > }> > if> (x->hoja) {> > return> nullptr;> > }> > return> BtreeSearch(x->niño[i], k);> }>

C

BtreeSearch(x, k)> > i = 1> > > // n[x] means number of keys in x node> > while> i ? n[x] and k ? keyi[x]> > do> i = i + 1> > if> i n[x] and k = keyi[x]> > then> return> (x, i)> > if> leaf [x]> > then> return> NIL> > else> > return> BtreeSearch(ci[x], k)>

Java

class> Node {> > int> n;> > int> [] key => new> int> [MAX_KEYS];> > Node[] child => new> Node[MAX_CHILDREN];> > boolean> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i => 0> ;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

Python3

class> Node:> > def> __init__(> self> ):> > self> .n> => 0> > self> .key> => [> 0> ]> *> MAX_KEYS> > self> .child> => [> None> ]> *> MAX_CHILDREN> > self> .leaf> => True> def> BtreeSearch(x, k):> > i> => 0> > while> i and k>= x.key[i]: i += 1 si i y k == x.key[i]: devuelve x si x.leaf: devuelve Ninguno devuelve BtreeSearch(x.child[i], k)>

C#

class> Node {> > public> int> n;> > public> int> [] key => new> int> [MAX_KEYS];> > public> Node[] child => new> Node[MAX_CHILDREN];> > public> bool> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

JavaScript

// Define a Node class with properties n, key, child, and leaf> class Node {> > constructor() {> > this> .n = 0;> > this> .key => new> Array(MAX_KEYS);> > this> .child => new> Array(MAX_CHILDREN);> > this> .leaf => false> ;> > }> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> > let i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

Ejemplos:

Aporte: Busque 120 en el árbol B dado.

Solución:

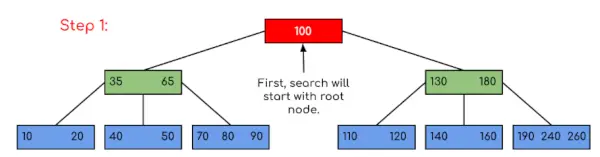
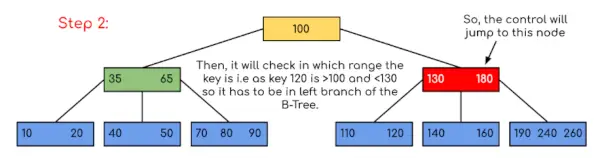
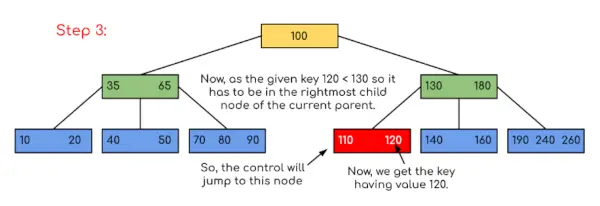
En este ejemplo, podemos ver que nuestra búsqueda se redujo simplemente limitando las posibilidades de que la clave que contiene el valor pueda estar presente. De manera similar, si en el ejemplo anterior tenemos que buscar 180, entonces el control se detendrá en el paso 2 porque el programa encontrará que la clave 180 está presente dentro del nodo actual. Y de manera similar, si busca 90, entonces 90 <100 irá automáticamente al subárbol izquierdo y, por lo tanto, el flujo de control será similar al que se muestra en el ejemplo anterior.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> > int> * keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode** C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> public> :> > BTreeNode(> int> _t,> bool> _leaf);> // Constructor> > // A function to traverse all nodes in a subtree rooted> > // with this node> > void> traverse();> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode*> > search(> int> k);> // returns NULL if k is not present.> > // Make the BTree friend of this so that we can access> > // private members of this class in BTree functions> > friend> class> BTree;> };> // A BTree> class> BTree {> > BTreeNode* root;> // Pointer to root node> > int> t;> // Minimum degree> public> :> > // Constructor (Initializes tree as empty)> > BTree(> int> _t)> > {> > root = NULL;> > t = _t;> > }> > // function to traverse the tree> > void> traverse()> > {> > if> (root != NULL)> > root->atravesar();> > }> > // function to search a key in this tree> > BTreeNode* search(> int> k)> > {> > return> (root == NULL) ? NULL : root->buscar(k);> > }> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(> int> _t,> bool> _leaf)> {> > // Copy the given minimum degree and leaf property> > t = _t;> > leaf = _leaf;> > // Allocate memory for maximum number of possible keys> > // and child pointers> > keys => new> int> [2 * t - 1];> > C => new> BTreeNode*[2 * t];> > // Initialize the number of keys as 0> > n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> > // There are n keys and n+1 children, traverse through n> > // keys and first n children> > int> i;> > for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->atravesar(); corte < < ' ' < < keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->atravesar(); } // Función para buscar la clave k en el subárbol enraizado con este nodo BTreeNode* BTreeNode::search(int k) { // Encuentra la primera clave mayor o igual a k int i = 0; mientras (i teclas[i]) i++; // Si la clave encontrada es igual a k, devuelve este nodo if (keys[i] == k) return this; // Si la clave no se encuentra aquí y este es un nodo hoja if (leaf == true) return NULL; // Ir al niño apropiado return C[i]->search(k); }>

Java

// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > System.out.println();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > boolean> > leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> boolean> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [> 2> * t -> 1> ];> > this> .C => new> BTreeNode[> 2> * t];> > this> .n => 0> ;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i => 0> ;> > for> (i => 0> ; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > System.out.print(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i => 0> ;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }>

Python3

# Create a node> class> BTreeNode:> > def> __init__(> self> , leaf> => False> ):> > self> .leaf> => leaf> > self> .keys> => []> > self> .child> => []> # Tree> class> BTree:> > def> __init__(> self> , t):> > self> .root> => BTreeNode(> True> )> > self> .t> => t> > # Insert node> > def> insert(> self> , k):> > root> => self> .root> > if> len> (root.keys)> => => (> 2> *> self> .t)> -> 1> :> > temp> => BTreeNode()> > self> .root> => temp> > temp.child.insert(> 0> , root)> > self> .split_child(temp,> 0> )> > self> .insert_non_full(temp, k)> > else> :> > self> .insert_non_full(root, k)> > # Insert nonfull> > def> insert_non_full(> self> , x, k):> > i> => len> (x.keys)> -> 1> > if> x.leaf:> > x.keys.append((> None> ,> None> ))> > while> i>> => 0> and> k[> 0> ] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 y k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Dividir el hijo def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] si no y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # Imprime el árbol def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') para i en x.keys: print(i, end=' ') print() l += 1 si len(x.child)> 0: para i en x.child: self.print_tree(i, l) # Clave de búsqueda en el árbol def search_key(self, k, x=Ninguno): si x no es Ninguno: i = 0 mientras i x.keys[i][0]: i += 1 si yo

C#

// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > Console.WriteLine();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> bool> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [2 * t - 1];> > this> .C => new> BTreeNode[2 * t];> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i = 0;> > for> (i = 0; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > Console.Write(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > public> BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i = 0;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by Rajput-Ji>

JavaScript

// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> > // Constructor (Initializes tree as empty)> > constructor(t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > > // function to traverse the tree> > traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > document.write(> ' '> );> > }> > > // function to search a key in this tree> > search(k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> > }> // A BTree node> class BTreeNode> {> > // Constructor> > constructor(t,leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> Array(2 * t - 1);> > this> .C => new> Array(2 * t);> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted with this node> > traverse()> > {> > // There are n keys and n+1 children, traverse through n keys> > // and first n children> > let i = 0;> > for> (i = 0; i <> this> .n; i++) {> > > // If this is not leaf, then before printing key[i],> > // traverse the subtree rooted with child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > document.write(keys[i] +> ' '> );> > }> > > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > > // A function to search a key in the subtree rooted with this node.> > search(k)> // returns NULL if k is not present.> > {> > > // Find the first key greater than or equal to k> > let i = 0;> > while> (i keys[i])> > i++;> > > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > > // If the key is not found here and this is a leaf node> > if> (leaf ==> true> )> > return> null> ;> > > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by patel2127>

Nota: El código anterior no contiene el programa del controlador. Cubriremos el programa completo en nuestra próxima publicación sobre Inserción del árbol B .

Hay dos convenciones para definir un árbol B, una es definir por grado mínimo y la segunda es definir por orden. Hemos seguido la convención de grado mínimo y seguiremos la misma en las próximas publicaciones en B-Tree. Los nombres de las variables utilizadas en el programa anterior también se mantienen iguales.

Aplicaciones de los árboles B:

• Se utiliza en grandes bases de datos para acceder a los datos almacenados en el disco.
• La búsqueda de datos en un conjunto de datos se puede lograr en mucho menos tiempo utilizando B-Tree
• Con la función de indexación, se puede lograr una indexación multinivel.
• La mayoría de los servidores también utilizan el enfoque de árbol B.
• Los B-Trees se utilizan en sistemas CAD para organizar y buscar datos geométricos.
• Los B-Trees también se utilizan en otras áreas, como el procesamiento del lenguaje natural, las redes informáticas y la criptografía.

Ventajas de los árboles B:

• Los B-Trees tienen una complejidad temporal garantizada de O(log n) para operaciones básicas como inserción, eliminación y búsqueda, lo que los hace adecuados para grandes conjuntos de datos y aplicaciones en tiempo real.
• Los árboles B se equilibran por sí solos.
• Alta concurrencia y alto rendimiento.
• Utilización eficiente del almacenamiento.

Desventajas de los árboles B:

• Los B-Trees se basan en estructuras de datos basadas en disco y pueden tener un uso elevado del disco.
• No es lo mejor para todos los casos.
• Lento en comparación con otras estructuras de datos.

Inserción y Eliminación:
Inserción del árbol B
Eliminación del árbol B