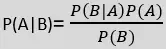Implementación de cifrado afín

El cifrado afín es un tipo de cifrado de sustitución monoalfabético en el que cada letra de un alfabeto se asigna a su equivalente numérico cifrado mediante una función matemática simple y se convierte nuevamente en una letra. La fórmula utilizada significa que cada letra se cifra en otra letra y viceversa, lo que significa que el cifrado es esencialmente un cifrado de sustitución estándar con una regla que rige qué letra va a cuál.
Todo el proceso se basa en el módulo de trabajo m (la longitud del alfabeto utilizado). En el cifrado afín, las letras de un alfabeto de tamaño m se asignan primero a los números enteros en el rango 0...m-1.
La 'clave' para el cifrado Affine consta de 2 números que los llamaremos a y b. La siguiente discusión supone el uso de un alfabeto de 26 caracteres (m = 26). a debe elegirse para que sea relativamente primo con m (es decir, a no debe tener factores en común con m).

Cifrado
Utiliza aritmética modular para transformar el número entero al que corresponde cada letra de texto plano en otro número entero que corresponde a una letra de texto cifrado. La función de cifrado para una sola letra es
E ( x ) = ( a x + b ) mod m modulus m: size of the alphabet a and b: key of the cipher. a must be chosen such that a and m are coprime.
Descifrado
Al descifrar el texto cifrado debemos realizar las funciones opuestas (o inversas) en el texto cifrado para recuperar el texto sin formato. Una vez más, el primer paso es convertir cada una de las letras del texto cifrado en sus valores enteros. La función de descifrado es
D ( x ) = a^-1 ( x - b ) mod m a^-1 : modular multiplicative inverse of a modulo m. i.e. it satisfies the equation 1 = a a^-1 mod m .
Para encontrar un inverso multiplicativo
Necesitamos encontrar un número x tal que:
Si encontramos el número x tal que la ecuación sea verdadera, entonces x es el inverso de a y lo llamamos a^-1. La forma más sencilla de resolver esta ecuación es buscar cada uno de los números del 1 al 25 y ver cuál satisface la ecuación.
[gxd] = gcd(am); % we can ignore g and d we dont need them x = mod(xm);
Si ahora multiplica x y a y reduce el resultado (mod 26), obtendrá la respuesta 1. Recuerde que esta es solo la definición de una inversa, es decir, si a*x = 1 (mod 26), entonces x es una inversa de a (y a es una inversa de x)
Ejemplo:

Implementación:
C++ //CPP program to illustrate Affine Cipher #include using namespace std ; //Key values of a and b const int a = 17 ; const int b = 20 ; string encryptMessage ( string msg ) { ///Cipher Text initially empty string cipher = '' ; for ( int i = 0 ; i < msg . length (); i ++ ) { // Avoid space to be encrypted if ( msg [ i ] != ' ' ) /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' ) ) + b ) % 26 ) + 'A' ); else //else simply append space character cipher += msg [ i ]; } return cipher ; } string decryptCipher ( string cipher ) { string msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; //Check if (a*i)%26 == 1 //then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . length (); i ++ ) { if ( cipher [ i ] != ' ' ) /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ msg = msg + ( char ) ((( a_inv * (( cipher [ i ] + 'A' - b )) % 26 )) + 'A' ); else //else simply append space character msg += cipher [ i ]; } return msg ; } //Driver Program int main ( void ) { string msg = 'AFFINE CIPHER' ; //Calling encryption function string cipherText = encryptMessage ( msg ); cout < < 'Encrypted Message is : ' < < cipherText < < endl ; //Calling Decryption function cout < < 'Decrypted Message is: ' < < decryptCipher ( cipherText ); return 0 ; }
Java // Java program to illustrate Affine Cipher class GFG { // Key values of a and b static int a = 17 ; static int b = 20 ; static String encryptMessage ( char [] msg ) { /// Cipher Text initially empty String cipher = '' ; for ( int i = 0 ; i < msg . length ; i ++ ) { // Avoid space to be encrypted /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ if ( msg [ i ] != ' ' ) { cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' )) + b ) % 26 ) + 'A' ); } else // else simply append space character { cipher += msg [ i ] ; } } return cipher ; } static String decryptCipher ( String cipher ) { String msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; // Check if (a*i)%26 == 1 // then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . length (); i ++ ) { /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ if ( cipher . charAt ( i ) != ' ' ) { msg = msg + ( char ) ((( a_inv * (( cipher . charAt ( i ) + 'A' - b )) % 26 )) + 'A' ); } else //else simply append space character { msg += cipher . charAt ( i ); } } return msg ; } // Driver code public static void main ( String [] args ) { String msg = 'AFFINE CIPHER' ; // Calling encryption function String cipherText = encryptMessage ( msg . toCharArray ()); System . out . println ( 'Encrypted Message is : ' + cipherText ); // Calling Decryption function System . out . println ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); } } // This code contributed by Rajput-Ji
Python # Implementation of Affine Cipher in Python # Extended Euclidean Algorithm for finding modular inverse # eg: modinv(7 26) = 15 def egcd ( a b ): x y u v = 0 1 1 0 while a != 0 : q r = b // a b % a m n = x - u * q y - v * q b a x y u v = a r u v m n gcd = b return gcd x y def modinv ( a m ): gcd x y = egcd ( a m ) if gcd != 1 : return None # modular inverse does not exist else : return x % m # affine cipher encryption function # returns the cipher text def affine_encrypt ( text key ): ''' C = (a*P + b) % 26 ''' return '' . join ([ chr ((( key [ 0 ] * ( ord ( t ) - ord ( 'A' )) + key [ 1 ] ) % 26 ) + ord ( 'A' )) for t in text . upper () . replace ( ' ' '' ) ]) # affine cipher decryption function # returns original text def affine_decrypt ( cipher key ): ''' P = (a^-1 * (C - b)) % 26 ''' return '' . join ([ chr ((( modinv ( key [ 0 ] 26 ) * ( ord ( c ) - ord ( 'A' ) - key [ 1 ])) % 26 ) + ord ( 'A' )) for c in cipher ]) # Driver Code to test the above functions def main (): # declaring text and key text = 'AFFINE CIPHER' key = [ 17 20 ] # calling encryption function affine_encrypted_text = affine_encrypt ( text key ) print ( 'Encrypted Text: {} ' . format ( affine_encrypted_text )) # calling decryption function print ( 'Decrypted Text: {} ' . format ( affine_decrypt ( affine_encrypted_text key ) )) if __name__ == '__main__' : main () # This code is contributed by # Bhushan Borole
C# // C# program to illustrate Affine Cipher using System ; class GFG { // Key values of a and b static int a = 17 ; static int b = 20 ; static String encryptMessage ( char [] msg ) { /// Cipher Text initially empty String cipher = '' ; for ( int i = 0 ; i < msg . Length ; i ++ ) { // Avoid space to be encrypted /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ if ( msg [ i ] != ' ' ) { cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' )) + b ) % 26 ) + 'A' ); } else // else simply append space character { cipher += msg [ i ]; } } return cipher ; } static String decryptCipher ( String cipher ) { String msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; // Check if (a*i)%26 == 1 // then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . Length ; i ++ ) { /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ if ( cipher [ i ] != ' ' ) { msg = msg + ( char ) ((( a_inv * (( cipher [ i ] + 'A' - b )) % 26 )) + 'A' ); } else //else simply append space character { msg += cipher [ i ]; } } return msg ; } // Driver code public static void Main ( String [] args ) { String msg = 'AFFINE CIPHER' ; // Calling encryption function String cipherText = encryptMessage ( msg . ToCharArray ()); Console . WriteLine ( 'Encrypted Message is : ' + cipherText ); // Calling Decryption function Console . WriteLine ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); } } /* This code contributed by PrinciRaj1992 */
JavaScript //Javascript program to illustrate Affine Cipher //Key values of a and b let a = 17 ; let b = 20 ; function encryptMessage ( msg ) { ///Cipher Text initially empty let cipher = '' ; for ( let i = 0 ; i < msg . length ; i ++ ) { // Avoid space to be encrypted if ( msg [ i ] != ' ' ) /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ cipher = cipher + String . fromCharCode (((( a * ( msg [ i ]. charCodeAt ( 0 ) - 65 ) ) + b ) % 26 ) + 65 ); else //else simply append space character cipher += msg [ i ]; } return cipher ; } function decryptCipher ( cipher ) { let msg = '' ; let a_inv = 0 ; let flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( let i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; //Check if (a*i)%26 == 1 //then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( let i = 0 ; i < cipher . length ; i ++ ) { if ( cipher [ i ] != ' ' ) /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ msg = msg + String . fromCharCode ((( a_inv * (( cipher [ i ]. charCodeAt ( 0 ) + 65 - b )) % 26 )) + 65 ); else //else simply append space character msg += cipher [ i ]; } return msg ; } //Driver Program let msg = 'AFFINE CIPHER' ; //Calling encryption function let cipherText = encryptMessage ( msg ); console . log ( 'Encrypted Message is : ' + cipherText ); //Calling Decryption function console . log ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); // The code is contributed by Arushi Jindal.
Producción
Encrypted Message is : UBBAHK CAPJKX Decrypted Message is: AFFINE CIPHER
Crear cuestionario