Fórmula a2 – b2

a 2 - b 2 fórmula en Álgebra es la fórmula básica en matemáticas utilizada para resolver diversos problemas algebraicos. a 2 - b 2 La fórmula también se llama fórmula de diferencia de cuadrados, ya que esta fórmula nos ayuda a encontrar la diferencia entre dos cuadrados sin tener que calcularlos realmente. La imagen agregada a continuación muestra la fórmula de un 2 - b 2

En este artículo, aprenderemos la a 2 - b 2 fórmula, una 2 - b 2 identidad, ejemplos y otros en detalle.
Tabla de contenidos
- ¿Qué es la fórmula a2 – b2?
- Fórmula de diferencia de cuadrados
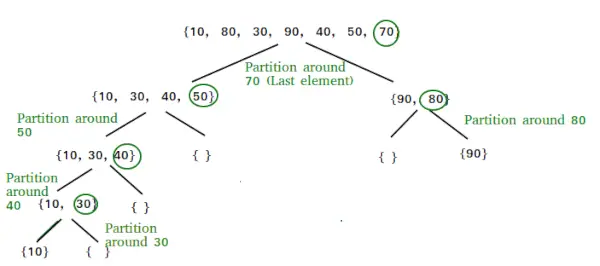
- a2 – b2 Prueba de fórmula cuadrada
- (a + b)2 y (a – b)2 Fórmula
- a2 – b2 Identidad
¿Qué es un 2 - b 2 ¿Fórmula?
a 2 - b 2 La fórmula en álgebra es la fórmula básica para resolver problemas algebraicos. También se utiliza para resolver problemas trigonométricos, diferenciales y otros. Esta fórmula nos dice que la diferencia entre dos números al cuadrado es igual al producto de la suma y la diferencia de dos números, es decir
a 2 - b 2 = (a + b).(a – b)
a 2 - b 2 Definición de fórmula
La fórmula a 2 - b 2 nos permite determinar la varianza entre los cuadrados de dos números sin la necesidad de calcular los valores cuadrados reales. La expresión para la a 2 - b 2 la fórmula es la siguiente: a 2 - b 2 = (a + b).(a – b)
Fórmula de diferencia de cuadrados
La diferencia de dos cuadrados se calcula utilizando la identidad algebraica estándar a 2 - b 2 . Por ejemplo, nos dan dos variables, a y b, luego la diferencia de sus cuadrados se calcula usando la fórmula, a 2 - b 2 = (a+b).(a–b)
Básicamente, la fórmula de diferencia de cuadrados dice que para dos variables algebraicas cualesquiera a y b, la expresión a 2 - b 2 es igual al producto de la suma por la diferencia de las variables. Esta identidad se utiliza ampliamente para simplificar expresiones algebraicas complicadas.
a 2 - b 2 Prueba de fórmula cuadrada
a 2 - b 2 La identidad se puede probar simplificando el RHS de la identidad. La A 2 - b 2 la fórmula se da como,
a 2 - b 2 = (a – b)(a + b)
Esta fórmula se demuestra como,
RHS = (a+b) (a–b)
⇒ RHS = a (a–b) + b (a–b)
⇒ DERECHO = a 2 – ab + ba – b 2
⇒ DERECHO = a 2 – ab + ab – b 2
⇒ DERECHO = a 2 - b 2
⇒ RD = IZQUIERDO
Por lo tanto probado.
a 2 +b 2 Fórmula
La A 2 +b 2 fórmula es la fórmula algebraica que se utiliza para encontrar la suma de los cuadrados de dos números. La suma de la fórmula cuadrada viene dada como,
a 2 +b 2 = (a+b) 2 – 2ab
La A 2 +b 2 La fórmula se utiliza para resolver varios problemas algebraicos. A continuación se agregan otras fórmulas algebraicas importantes,
(a+b) 2 y (a-b) 2 Fórmula
El (a+b) 2 la fórmula se da como,
(a+b) 2 = un 2 +b 2 + 2 ab
El (a-b) 2 la fórmula se da como,
(a-b) 2 = un 2 +b 2 – 2ab
a 2 - b 2 Identidad
a 2 - b 2 La identidad es una de las identidades algebraicas que se utiliza para encontrar la diferencia entre los cuadrados de dos números. Esta identidad tiene varias aplicaciones y se da como,
a 2 - b 2 = (a – b).(a + b)
Leer más,
- Fórmula de álgebra
- Fórmula matemática básica
- Expresión algebraica
Ejemplos en un 2 - b 2 Fórmula
Ejemplo 1: simplificar x 2 – 16
Solución:
=x 2 – 16
=x 2 – 4 2
Lo sabemos, a 2 - b 2 = (a+b) (a–b)
Dado,
- un = x
- segundo = 4
= (x + 4)(x – 4)
Ejemplo 2: simplificar 9 años 2 – 144
Solución:
= 9 años 2 – 144
= (3 años) 2 – (12) 2
Lo sabemos, a 2 - b 2 = (a+b)(a–b)
Dado,
- a = 3 años
- segundo = 12
= (3y + 12)(3y – 12)
Ejemplo 3: Simplificar (3x + 2) 2 – (3x – 2) 2
Solución:
Lo sabemos,
a 2 - b 2 = (a+b)(a–b)
Dado,
- a = 3x + 2
- segundo = 3x – 2
(3x + 2) 2 – (3x – 2) 2
= (3x + 2 + 3x – 2)(3x + 2 – (3x – 2))
= 6x(3x + 2 – 3x + 2)
= 6x(4)
= 24x
Example 4: Simplify y 2 – 100
Solución:
= y 2 – 100
= y 2 – (10) 2
Lo sabemos,
a 2 - b 2 = (a+b)(a–b)
Dado,
- a = y
- segundo = 10
= (y + 10)(y – 10)
Ejemplo 5: Evaluar (x + 6) (x – 6)
Solución:
Lo sabemos,
(a+b) (a–b) = a 2 - b 2
Dado,
- un = x
- segundo = 6
(x + 6) (x – 6)
=x 2 – 6 2
=x 2 – 36
Example 6: Evaluate (y + 13)(y – 13)
Solución:
Lo sabemos,
(a+b) (a–b) = a 2 - b 2
Dado,
- a = y
- segundo = 13
(y + 13).(y – 13)
= y 2 – (13) 2
= y 2 – 169
Ejemplo 7: Evaluar (x + y + z).(x + y – z)
Solución:
Lo sabemos,
(a+b) (a–b) = a 2 - b 2
Dado,
- a = x + y
- segundo = z
(x + y + z) (x + y – z)
= (x + y) 2 - Con 2
=x 2 + y 2 + 2xy – z 2
(a 2 - b 2 ) Fórmula – Hoja de trabajo
P1. Simplifica 15 2 – 14 2 usando un 2 - b 2 identidad.
P2. Simplifica 11 2 – 7 2 usando un 2 - b 2 identidad.
P3. Resuelve 23 2 – 9 2 usando un 2 - b 2 identidad.
P4. Resuelve 9 2 – 7 2 usando un 2 - b 2 identidad.
a 2 - b 2 Fórmula – Preguntas frecuentes
1. ¿Qué es un 2 − segundo 2 ?
a 2 - b 2 fórmula es la fórmula que se utiliza para encontrar la diferencia entre dos cuadrados sin encontrar realmente el cuadrado. La A 2 - b 2 la fórmula es,
a 2 - b 2 = (a + b)(a – b)
2. ¿Qué es la ley de un 2 b 2 ¿Fórmula?
ley de un 2 b 2 las fórmulas son,
- a 2 - b 2 = (a + b)(a – b)
- a 2 +b 2 = (a+b) 2 – 2ab
3. ¿Qué es un 2 b 2 ¿Fórmula utilizada para?
a 2 b 2 La fórmula se utiliza para resolver diversos problemas algebraicos y también se utiliza para simplificar problemas trigonométricos, de cálculo y de integración.
4. ¿Qué es un 2 b 2 ¿Fórmula?
Hay dos un 2 b 2 fórmulas que son, una 2 +b 2 , y un 2 - b 2 la fórmula de expansión para un 2 b 2 las fórmulas se dan como,
- a 2 - b 2 = (a + b)(a – b)
- a 2 +b 2 = (a+b) 2 – 2ab
5. ¿Cuándo es un 2 - b 2 ¿Se utiliza la fórmula?
a 2 - b 2 La fórmula se utiliza para encontrar la diferencia entre los cuadrados de dos números sin encontrar realmente los cuadrados. Esta fórmula también se utiliza para resolver diversos problemas algebraicos, trigonométricos y de otro tipo.