Mindestsegmente in der Sieben-Segment-Anzeige
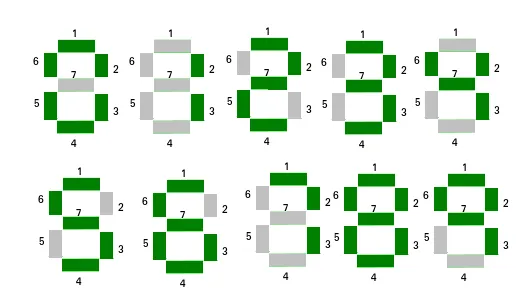
Zur Anzeige von Zahlen kann eine Sieben-Segment-Anzeige verwendet werden. Gegeben eine Reihe von N natürliche Zahlen. Die Aufgabe besteht darin, die Zahl im Array zu finden, die die minimale Anzahl von Segmenten verwendet, um die Zahl anzuzeigen. Wenn mehrere Zahlen eine Mindestanzahl an Segmenten haben, wird die Zahl mit dem kleinsten Index ausgegeben.

Beispiele:
Eingabe: arr[] = { 1 2 3 4 5 }.
Ausgabe : 1
Erläuterung: Das Element, das die minimale Anzahl von Segmenten verwendet, ist 1 (d. h. 2 Segmente).Eingabe: arr[] = { 489 206 745 123 756 }.
Ausgabe : 745
Erläuterung: Das Element mit dem kleinsten Index, das die minimale Anzahl von Segmenten verwendet, ist 745 (d. h. 12 Segmente).
Die Idee besteht darin, die Anzahl der von den Ziffern 0 bis 9 verwendeten Segmente vorab zu berechnen und zu speichern. Summieren Sie nun für jedes Element des Arrays die Anzahl der Segmente, die von jeder Ziffer verwendet werden. Suchen Sie dann das Element, das die minimale Anzahl an Segmenten verwendet.
C++Die Anzahl der von Ziffer verwendeten Segmente:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include using namespace std ; // Precomputed values of segment used by digit 0 to 9. const int seg [ 10 ] = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } int elementMinSegment ( vector < int > arr int n ) { // Initialising the minimum segment and minimum // number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } int main () { vector < int > arr = { 489 206 745 123 756 }; int n = arr . size (); cout < < elementMinSegment ( arr n ) < < endl ; return 0 ; }
Java import java.io.* ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ] ; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ] ; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ] ); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ] ); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ] ; } static public void main ( String [] args ) { int [] arr = { 489 206 745 123 756 }; int n = arr . length ; System . out . println ( elementMinSegment ( arr n )); } }
Python # Precomputed values of segment # used by digit 0 to 9. seg = [ 6 2 5 5 4 5 6 3 7 6 ] # Return the number of # segments used by x. def computeSegment ( x ): if ( x == 0 ): return seg [ 0 ] count = 0 # Finding sum of the segment # used by each digit of a number. while ( x ): count += seg [ x % 10 ] x = x // 10 return count # function to return minimum sum index def elementMinSegment ( arr n ): # Initialising the minimum # segment and minimum number index. minseg = computeSegment ( arr [ 0 ]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range ( 1 n ): temp = computeSegment ( arr [ i ]) # If arr[i] used less segment # then update minimum segment # and minimum number. if ( temp < minseg ): minseg = temp minindex = i return arr [ minindex ] # Driver Code arr = [ 489 206 745 123 756 ] n = len ( arr ) # function print required answer print ( elementMinSegment ( arr n )) # This code is contributed by # Sanjit_Prasad
C# using System ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = new int [ 10 ]{ 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } static public void Main () { int [] arr = { 489 206 745 123 756 }; int n = arr . Length ; Console . WriteLine ( elementMinSegment ( arr n )); } }
JavaScript // Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6 ]; // Return the number of segments used by x. function computeSegment ( x ) { if ( x == 0 ) return seg [ 0 ]; let count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x = parseInt ( x / 10 10 ); } return count ; } function elementMinSegment ( arr n ) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment ( arr [ 0 ]); let minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( let i = 1 ; i < n ; i ++ ) { let temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr . length ; console . log ( elementMinSegment ( arr n ));
Ausgabe
745
Zeitkomplexität: O(n * log 10 N)
Hilfsraum: O(10)