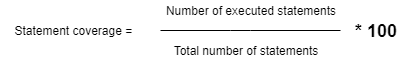WIE FINDE ICH DIE STANDARDABWEICHUNG IN R?

In diesem Artikel besprechen wir, wie man die Standardabweichung findet Programmiersprache R . Die Standardabweichung R ist das Maß für die Streuung der Werte. Sie kann auch als Quadratwurzel der Varianz definiert werden.

Formel der Stichprobenstandardabweichung:

$s = sqrt{frac{1}{N-1}displaystylesumlimits_{i=1}^N(x_i-overline{x})^2 }$

Wo,

s = Stichprobenstandardabweichung
N = Anzahl der Entitäten
= Mittelwert der Entitäten

Grundsätzlich gibt es zwei verschiedene Möglichkeiten, die Standardabweichung in der Programmiersprache R zu berechnen. Beide werden im Folgenden erläutert.

Methode 1: Naiver Ansatz

Bei dieser Methode zur Berechnung der Standardabweichung verwenden wir die obige Standardformel der Stichprobenstandardabweichung in der Sprache R.

Beispiel 1:

R

v <-> c> (12,24,74,32,14,29,84,56,67,41)> s <-> sqrt> (> sum> ((v-> mean> (v))^2/(> length> (v)-1)))> print> (s)>

Ausgabe:

[1]   25.53886

Beispiel 2:

R

v <-> c> (1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9)> s <-> sqrt> (> sum> ((v-> mean> (v))^2/(> length> (v)-1)))> print> (s)>

Ausgabe:

[1] 2.676004

Methode 2: Verwendung von sd()

Die Funktion sd() wird verwendet, um die Standardabweichung zurückzugeben.

Syntax: sd(x, na.rm = FALSCH)

Parameter:

x: ein numerischer Vektor, eine Matrix oder ein Datenrahmen.na.rm: Fehlende Werte entfernt werden?

Zurückkehren: Die Stichprobenstandardabweichung von x.

Beispiel 1:

R

v <-> c> (12,24,74,32,14,29,84,56,67,41)> s <-> sd> (v)> print> (s)>

Ausgabe:

[1] 25.53886

Beispiel 2:

R

v <-> c> (71,48,98,65,45,27,39,61,50,24,17)> s1 <-> sqrt> (> sum> ((v-> mean> (v))^2/(> length> (v)-1)))> print> (s1)> s2 <-> sd> (v)> print> (s2)>

Ausgabe:

[1] 23.52175

Beispiel 3:

R

v <-> c> (1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9)> s1 <-> sqrt> (> sum> ((v-> mean> (v))^2/(> length> (v)-1)))> print> (s1)> s2 <-> sd> (v)> print> (s2)>

Ausgabe:

[1] 2.676004

Berechnen Sie die Standardabweichung des Datenrahmens:

Mit beiden Methoden können wir die Standardabweichung des Datenrahmens berechnen. Wir können den Iris-Datensatz nehmen und für jede Spalte die Standardabweichung berechnen.

Beispiel 1:

R

data> (iris)> sd> (iris$Sepal.Length)> sd> (iris$Sepal.Width)> sd> (iris$Petal.Length)> sd> (iris$Petal.Width)>

Ausgabe:

[1] 0.8280661 [1] 0.4358663 [1] 1.765298 [1] 0.7622377

Mit Hilfe der Apply-Funktion können wir auch die Standardabweichung für den gesamten Datenrahmen berechnen.

R

# Load the iris dataset> data> (iris)> # Calculate the standard deviation for each column> std_deviation <-> apply> (iris[, 1:4], 2, sd)> # Display the standard deviation values> print> (std_deviation)>

Ausgabe:

Sepal.Length Sepal.Width Petal.Length Petal.Width 0.8280661 0.4358663 1.7652982 0.7622377

Die Spalten 1 bis 4 des Iris-Datensatzes, bei denen es sich um die numerischen Spalten mit den Variablenmessungen handelt, werden mit dem Ausdruck iris[, 1:4] im obigen Code ausgewählt.

Die SD-Funktion wird mithilfe der Apply-Funktion auf jede Spalte (mit 2 markiert) der ausgewählten Teilmenge des Iris-Datensatzes angewendet. Die resultierenden Standardabweichungswerte werden im std_deviation-Vektor für jede Spalte gespeichert.