Prüfen Sie, ob ein Punkt im Kreissektor existiert oder nicht.
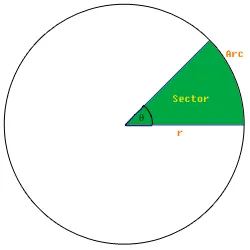
Wir haben einen Kreis mit Mittelpunkt im Ursprung (0 0). Als Eingabe erhalten wir den Startwinkel des Kreissektors und die Größe des Kreissektors in Prozent.
Beispiele:
Input : Radius = 8 StartAngle = 0 Percentage = 12 x = 3 y = 4 Output : Point (3 4) exists in the circle sector Input : Radius = 12 Startangle = 45 Percentage = 25 x = 3 y = 4 Output : Point (3 4) does not exist in the circle sector
 Quelle: Wikibook.org
Quelle: Wikibook.org
In diesem Bild beträgt der Startwinkel den Radius r von 0 Grad. Nehmen wir an, dass der Prozentsatz der farbigen Fläche 12 % beträgt, dann berechnen wir den Endwinkel als 360/Prozent + Startwinkel .
Um herauszufinden, ob ein Punkt (x y) in einem Kreissektor (zentriert im Ursprung) existiert oder nicht, ermitteln wir die Polarkoordinaten dieses Punktes und führen dann die folgenden Schritte durch:
- Konvertieren Sie damit xy in Polarkoordinaten
Winkel = Abwesenheit(y/x); Radius = sqrt(x * y y y y y); - Dann muss der Winkel zwischen StartingAngle und EndingAngle liegen und der Radius zwischen 0 und Ihrem Radius.
// C++ program to check if a point lies inside a circle // sector. #include using namespace std ; void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates float polarradius = sqrt ( x * x + y * y ); float Angle = atan ( y / x ); // Check whether polarradius is less then radius of circle // or not and Angle is between startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) printf ( 'Point (%d %d) exist in the circle sector n ' x y ); else printf ( 'Point (%d %d) does not exist in the circle sector n ' x y ); } // Driver code int main () { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); return 0 ; }
Java // Java program to check if // a point lies inside a circle // sector. class GFG { static void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates double polarradius = Math . sqrt ( x * x + y * y ); double Angle = Math . atan ( y / x ); // Check whether polarradius is // less then radius of circle // or not and Angle is between // startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) System . out . print ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); else System . out . print ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); } // Driver Program to test above function public static void main ( String arg [] ) { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); } } // This code is contributed // by Anant Agarwal.
Python3 # Python3 program to check if a point # lies inside a circle sector. import math def checkPoint ( radius x y percent startAngle ): # calculate endAngle endAngle = 360 / percent + startAngle # Calculate polar co-ordinates polarradius = math . sqrt ( x * x + y * y ) Angle = math . atan ( y / x ) # Check whether polarradius is less # then radius of circle or not and # Angle is between startAngle and # endAngle or not if ( Angle >= startAngle and Angle <= endAngle and polarradius < radius ): print ( 'Point (' x '' y ') ' 'exist in the circle sector' ) else : print ( 'Point (' x '' y ') ' 'does not exist in the circle sector' ) # Driver code radius x y = 8 3 4 percent startAngle = 12 0 checkPoint ( radius x y percent startAngle ) # This code is contributed by # Smitha Dinesh Semwal
C# // C# program to check if a point lies // inside a circle sector. using System.IO ; using System ; class GFG { static void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates float polarradius = ( float ) Math . Sqrt ( x * x + y * y ); float Angle = ( float ) Math . Atan ( y / x ); // Check whether polarradius is less then // radius of circle or not and Angle is // between startAngle and endAngle or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) Console . Write ( 'Point ({0} {1}) exist in ' + 'the circle sector' x y ); else Console . Write ( 'Point ({0} {1}) does not ' + 'exist in the circle sector' x y ); } // Driver code public static void Main () { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); } } // This code is contributed by Smitha Dinesh Semwal
JavaScript < script > // Javascript program to check if // a point lies inside a circle // sector. function checkPoint ( radius x y percent startAngle ) { // Calculate endAngle let endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates let polarradius = Math . sqrt ( x * x + y * y ); let Angle = Math . atan ( y / x ); // Check whether polarradius is // less then radius of circle // or not and Angle is between // startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) document . write ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); else document . write ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); } // Driver code let radius = 8 x = 3 y = 4 ; let percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); // This code is contributed by splevel62 < /script>
Ausgabe :
Point(3 4) exists in the circle sector
Zeitkomplexität: O(1)
Hilfsraum: O(1)