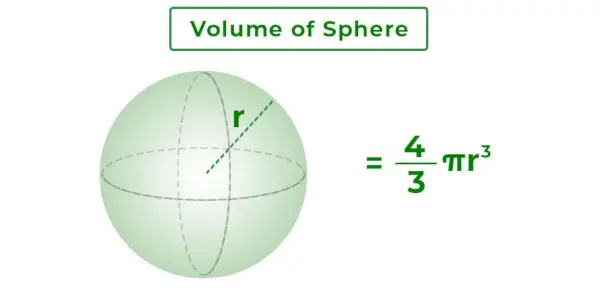
Volumen af ​​en kugle er mængden af ​​væske en kugle kan indeholde. Formlen for kuglevolumen er givet som 4/3πr ³ . Det er det rum, der optages af en kugle i det 3-dimensionelle rum. Det måles i enhed ³ dvs. m ³ , cm ³ osv. En kugle er et tredimensionelt fast objekt med en rund form i geometrien.

Kuglens rumfang er det samlede rum, der optages af kuglens overflade, og det er proportionalt med terningen af ​​kuglens radius. I denne artikel vil vi lære om Volume of Sphere, Volume of Sphere Formel, Volume of Sphere Formel eksempler og andre i detaljer.

• Hvad er volumen af ​​en kugle?
• Volume of Sphere Formel
• Volumen af ​​en fast kugle
• Volumen af ​​en hul kugle
• Volumen af ​​sfæreformelafledning
• Hvordan beregnes volumen af ​​kugle?

Hvad er volumen af ​​en kugle?

Rumfanget af en kugle er mængden af ​​plads, den fylder i den. Kuglen er en tredimensionel rund fast form, hvor alle punkter på dens overflade er lige adskilt fra dens centrum. Den faste afstand er kuglens radius, og det faste punkt er kuglens centrum. Vi vil bemærke en ændring i form, når cirklen drejes. Som et resultat af rotationen af ​​det todimensionelle objekt kendt som en cirkel, opnås den tredimensionelle form af en kugle.

Lær mere,

• Kugle
• Sfærens overfladeareal

Volumen af ​​en sfære Definition

Rumfanget af en kugle er den samlede masse, der er omsluttet af kuglens overflade. Det er 3D-rummet inde i kuglen. Det afhænger af kuglens radius. Billedet tilføjet nedenfor viser en kugle med radius r og dens volumen.

Volume of Sphere Formel

Formel for kuglevolumen er den formel, der bruges til at finde kuglens rumfang, når dens radius er givet. Formlen for kuglevolumen for kuglen med radius R tilføjes nedenfor,

Rumfang af kugleformel = 4/3πr ³

Hvor,

• r er en kugles radius
• Pi er en konstant, og dens værdi er 22/7

En sfære er generelt kategoriseret i to, der er,

• Volumen af ​​solid kugle
• Volumen af ​​hul kugle

Lad os lære om dem i detaljer.

Volumen af ​​en fast kugle

En solid kugle er en kugle, der er helt fyldt indtil inde. dvs. den har masse indtil sin kerne og dens formel for volumen, når dens radius er r er,

Volumen af ​​en fast kugle(V) = (4/3)πr ³

Volumen af ​​en hul kugle

For en hul kugle er dens indre rum tomt, og antag at dens ydre radius er det R og dens indre radius er r, derefter beregnes dens volumen ved hjælp af formlen,

Volumen af ​​hul kugle = (4/3)π(R ³ – r ³ )

Volumen af ​​sfæreformelafledning

Formlen for kuglevolumen kan udledes ved hjælp af følgende metoder:

• Brug af integration
• Brug af Archimedes forhold mellem cylinder, kegle og kugle

Lad os diskutere disse metoder i detaljer som følger:

Volumen af ​​sfære ved hjælp af integration

Ved hjælp af integrationstilgangen kan vi simpelthen beregne volumenet af en kugle.

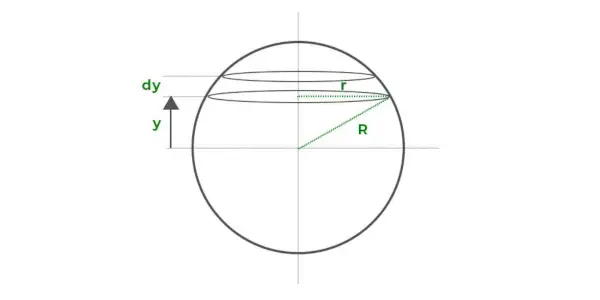
Antag, at kuglens volumen består af en række tynde cirkulære skiver stablet oven på hinanden, som tegnet i diagrammet ovenfor. Hver tynd skive har en radius på r og en tykkelse på dy, der er y afstand fra x-aksen.

Lad lydstyrken på en disk være dV. Værdien af ​​dV er givet ved,

dV = (πr ² ) dig

Således er dV = π (R ² - og ² ) dig

Kuglens samlede volumen vil være summen af ​​volumen af ​​alle disse små skiver. Den nødvendige værdi kan opnås ved at integrere udtrykket fra grænse -R til R.

Så kuglens volumen bliver,

V = int_{y=-R}^{y=R} dV

⇒ V = int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V = pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V = pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V = pi left[2R^3-frac{2R^3}{3} ight]

⇒ V = frac{4}{3}pi R^3

Således er formlen for kuglevolumen udledt.

Volumen af ​​sfære ved hjælp af Archimedes-relationer

Som Archimedes allerede har bevist, hvis en kegle, en kugle og en cylinder har samme radius r og samme højde, er deres volumener i forholdet 1:2:3.

Derfor kan vi sige:

Volumen af ​​cylinder = volumen af ​​kegle + volumen af ​​sfære

Således volumen af ​​kugle = volumen af ​​cylinder – volumen af ​​kegle

Som vi ved, er cylindervolumenet = πr ² h og volumen af ​​kegle = (1/3)πr ² h

Ved at indsætte disse værdier i ligningen får vi:

Rumfang af sfære = πr ² h – (1/3)πr ² h = (2/3)πr ² h

Vi antager, at cylinderens højde er lig med kuglens diameter, som er 2r. Dermed:

Kuglens volumen er (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Tjek også

• Formel med sfærisk hættevolumen
• Formel for sfærisk sektor
• Formel for sfærisk segment

Hvordan beregnes volumen af ​​kugle?

Kuglevolumen er det rum, som en kugle optager. Dens volumen kan beregnes ved hjælp af formlen V = 4/3πr ³ .

De nødvendige trin for at beregne volumenet af en kugle er:

Trin 1: Marker værdien af ​​kuglens radius.

2. september: Find terningen af ​​radius.

Trin 3: Multiplicer terningen af ​​radius med (4/3)π

Trin 4: Tilføj (enheden) ³ til det endelige svar.

Eksempel til beregning af kuglevolumen

Eksempel: Find rumfanget af en kugle med en radius på 7 cm.

Givet, r = 7 cm

V = (4/3)πr ³

Kuglens volumen, V = ((4/3) × π × 7 ³ ) cm ³

Højde = 1436,8 cm ³

Således er kuglens rumfang 1436,8 cm ³

Læs mere

• Volumen af ​​kegle
• Volumen af ​​terning
• Volumen af ​​cylinder

Volumen af ​​sfæreeksempler

Eksempel 1. Find rumfanget af kuglen, hvis radius er 9 cm.

Løsning:

Vi har, r = 9

Kuglens rumfang = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (9) (9) (9)

⇒ Kuglevolumen = (4) (3.14) (3) (9) (9)

⇒ Kuglens rumfang = 3052 cm ³

Eksempel 2. Find rumfanget af kuglen, hvis radius er 12 cm.

Løsning:

Vi har, r = 12

Kuglens rumfang = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (12) (12) (12)

⇒ Kuglens volumen = (4) (3.14) (4) (12) (12)

⇒ Kuglevolumen = 7234,56 cm ³

Eksempel 3. Find rumfanget af kuglen, hvis radius er 6 cm.

Løsning:

Vi har, r = 6

Kuglens rumfang = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (6) (6) (6)

⇒ Kuglevolumen = (4) (3.14) (2) (6) (6)

⇒ Kuglevolumen = 904,32 cm ³

Eksempel 4. Find rumfanget af kuglen, hvis radius er 4 cm.

Løsning:

Vi har, r = 4

Kuglens rumfang = 4/3 πr3

⇒ Kuglevolumen = (4/3) (3,14) (4) (4) (4)

⇒ Kuglevolumen = (1,33) (3,14) (4) (4) (4)

⇒ Kuglens rumfang = 267,27 cm ³

Eksempel 5. Find rumfanget af kuglen, hvis diameter er 10 cm.

Løsning:

Vi har 2r = 10

⇒ r = 5

Rumfang af kugle = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (5) (5) (5)

⇒ Kuglevolumen = (1,33) (3,14) (5) (5) (5)

⇒ Kuglens rumfang = 522,025 cm ³

Eksempel 6. Find rumfanget af kuglen, hvis diameter er 16 cm.

Løsning:

Vi har 2r = 16

⇒ r = 8

Kuglens rumfang = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (8) (8) (8)

⇒ Kuglevolumen = (1,33) (3,14) (8) (8) (8)

⇒ Kuglens rumfang = 2138,21 cm ³

Eksempel 7. Find rumfanget af kuglen, hvis diameter er 14 cm.

Løsning:

Vi har 2r = 14

⇒ r = 7

Kuglens rumfang = 4/3 πr ³

⇒ Kuglevolumen = (4/3) (3,14) (7) (7) (7)

⇒ Kuglevolumen = (1,33) (3,14) (7) (7) (7)

⇒ Kuglens rumfang = 1432,43 cm ³

Volumen af ​​sfære-praksisspørgsmål

Q1: Find rumfanget af kuglen, hvis diameter er 34 cm.

Q2: Find rumfanget af den hule kugle, hvis indre er 4 cm og ydre radius er 8 cm.

Q3: Find rumfanget af kuglen, hvis radius er 14 cm.

Q4: Hvad er rumfanget af en kugle, hvis radius er lig med siden af ​​kvadratet med areal 144 m ² .

Mængde af Sphere-Ofte stillede spørgsmål

Hvad er volumen af ​​sfære?

Rumfang af sfære er det rum, der optages af kuglens overflade.

Hvad er overfladearealet af en kugleformel?

Samlet overfladeareal af kuglen med radius r er, Areal = 4πr ²

Hvad er formlen for rumfanget af en kugle?

Volumen af ​​en kugle med radius r er, Volumen = 4/3πr ³

Hvordan finder vi rumfanget af halvkuglen?

Volumen af ​​en halvkugle med radius r er, Volumen = 2/3πr ³

Hvad er forholdet mellem volumen af ​​kugle og halvkugle?

Hvis en kugle og en halvkugle har samme radier, er forholdet mellem deres volumen,

I ₁ : IN ₂ = (4/3πr ³ ): (2/3πr ³ ) = 2 : 1

Hvad er volumenenheden for en kugle?

Kuglens rumfang måles i m ³ , cm ³ , liter osv. m ³ er standardmåleenheden.

Hvad er kuglens volumen, når dens radius er halveret?

Kuglens volumen = (4/3)πr ³ = (4/3)π(r/2) ³ = (4/3)π(r ³ /8) = Bind/8. Så kuglens volumen bliver en ottendedel.