Topologisk sortering

Topologisk sortering til Instrueret acyklisk graf (DAG) er en lineær rækkefølge af toppunkter, således at for hver rettet kant u-v, toppunkt i kommer før i i bestillingen.
Bemærk: Topologisk sortering for en graf er ikke mulig, hvis grafen ikke er en DAG .
Eksempel:
Anbefalet praksis DFS baseret løsning til at finde en topologisk sortering er allerede blevet diskuteret.Input: Graf:

Eksempel
Produktion: 5 4 2 3 1 0
Forklaring: Det første toppunkt i topologisk sortering er altid et toppunkt med en in-grad på 0 (et toppunkt uden indgående kanter). En topologisk sortering af følgende graf er 5 4 2 3 1 0. Der kan være mere end én topologisk sortering for en graf. En anden topologisk sortering af følgende graf er 4 5 2 3 1 0.
Topologisk rækkefølge er muligvis ikke unik:
Topologisk sortering er et afhængighedsproblem, hvor fuldførelsen af en opgave afhænger af afslutningen af flere andre opgaver, hvis rækkefølge kan variere. Lad os forstå dette koncept via et eksempel:
Antag, at vores opgave er at nå vores skole, og for at nå dertil, skal vi først klæde os på. Afhængighederne af at bære tøj er vist i nedenstående afhængighedsgraf. For eksempel kan du ikke have sko på, før du har sokker på.

Fra ovenstående billede ville du allerede have indset, at der findes flere måder at klæde sig på, billedet nedenfor viser nogle af disse måder.

Kan du liste al mulig topologisk rækkefølge at klæde sig på til ovenstående afhængighedsgraf?
Algoritme til topologisk sortering ved hjælp af DFS:
Her er en trin-for-trin algoritme til topologisk sortering ved hjælp af Depth First Search (DFS):
- Lav en graf med n hjørner og m -rettede kanter.
- Initialiser en stak og en besøgt række af størrelse n .
- For hvert ubesøgt toppunkt i grafen skal du gøre følgende:
- Kald DFS-funktionen med toppunktet som parameter.
- I DFS-funktionen skal du markere toppunktet som besøgt og rekursivt kalde DFS-funktionen for alle ubesøgte naboer til toppunktet.
- Når alle naboerne er blevet besøgt, skubbes toppunktet på stakken.
- Når alt kommer til alt, er hjørner blevet besøgt, pop elementer fra stakken og føj dem til outputlisten, indtil stakken er tom.
- Den resulterende liste er den topologisk sorterede rækkefølge af grafen.
Illustration Topologisk sorteringsalgoritme:
Nedenstående billede er en illustration af ovenstående fremgangsmåde:

Overordnet arbejdsgang af topologisk sortering
Trin 1:
- Vi starter DFS fra node 0, fordi den har nul indgående noder
- Vi skubber node 0 i stakken og flytter til næste node med minimum antal tilstødende noder, dvs. node 1.

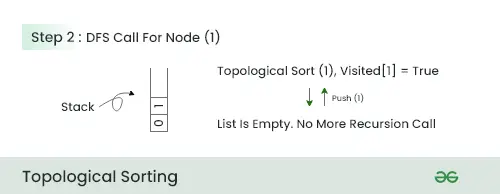
Trin 2:
- I dette trin, fordi der ikke er nogen ved siden af denne node, så skub node 1 i stakken og flyt til næste node.
Trin 3:
- I dette trin vælger vi node 2, fordi den har minimum antal tilstødende noder efter 0 og 1.
- Vi kalder DFS for node 2 og skubber alle de noder, som kommer i gennemløb fra node 2 i omvendt rækkefølge.
- Så tryk 3 og derefter 2.

Trin 4:
- Vi kalder nu DFS for node 4
- Fordi 0 og 1 allerede er til stede i stakken, så vi skubber bare node 4 i stakken og vender tilbage.

Trin 5:
- I dette trin, fordi alle de tilstødende noder på 5 allerede er i stakken, skubber vi node 5 i stakken og vender tilbage.

Trin 6: Dette er det sidste trin i den topologiske sortering, hvor vi henter alt element fra stakken og udskriver det i den rækkefølge.
Nedenfor er implementeringen af ovenstående tilgang:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector >& adj, vektor & besøgt, stak & Stack) { // Marker den aktuelle node som besøgt besøgt[v] = sand; // Gentag for alle tilstødende hjørner for (int i : adj[v]) { if (!besøgt[i]) topologiskSortUtil(i, adj, besøgt, stak); } // Skub nuværende toppunkt til stak, som gemmer resultatet Stack.push(v); } // Funktion til at udføre Topologisk Sortering void topologicalSort(vector >& adj, int V) { stak Stak; // Stak for at gemme resultatvektoren besøgt(V, falsk); // Kald den rekursive hjælpefunktion for at gemme // Topologisk sortering startende fra alle hjørner en efter // en for (int i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout < < Stack.top() < < ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector > kanter = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Graf repræsenteret som en nabolistevektor > adj(V); for (auto i : kanter) { adj[i[0]].push_back(i[1]); } cout < < 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List > adj, boolean[] besøgt, stak stack) { // Marker den aktuelle node som besøgt besøgt[v] = sand; // Gentag for alle tilstødende hjørner for (int i : adj.get(v)) { if (!besøgt[i]) topologiskSortUtil(i, adj, besøgt, stak); } // Skub det aktuelle toppunkt til stakken, som gemmer // resultatet stack.push(v); } // Funktion til at udføre Topologisk Sort statisk tomrum topologiskSort(List > adj, int V) { // Stak for at gemme resultatet Stak stak = ny stak(); boolean[] visited = new boolean[V]; // Kald den rekursive hjælpefunktion for at gemme // Topologisk sortering startende fra alle hjørner en // efter en for (int i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List > edges = new ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // Graf repræsenteret som en tilstødende liste Liste > adj = ny ArrayList(V); for (int i = 0; i < V; i++) { adj.add(new ArrayList()); } for (List i : edges) { adj.get(i.get(0)).add(i.get(1)); } topologiskSort(adj, V); } }
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V) C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List > adj, bool[] besøgt, stak stack) { // Marker den aktuelle node som besøgt besøgt[v] = sand; // Gentages for alle tilstødende hjørner foreach(int i i adj[v]) { if (!besøgt[i]) TopologiskSortUtil(i, adj, besøgt, stak); } // Skub det aktuelle toppunkt til stakken, som gemmer // resultatstakken. Push(v); } // Funktion til at udføre Topologisk Sort statisk tomrum TopologiskSort(List > adj, int V) { // Stak for at gemme resultatet Stak stak = ny stak (); bool[] besøgt = ny bool[V]; // Kald den rekursive hjælpefunktion for at gemme // Topologisk sortering startende fra alle hjørner en // efter en for (int i = 0; i < V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Driverkode static void Main(string[] args) { // Antal noder int V = 4; // Kantliste > kanter = ny liste >{ ny liste { 0, 1 }, ny liste { 1, 2 }, ny liste { 3, 1 }, ny liste { 3, 2 } }; // Graf repræsenteret som en tilstødende liste Liste > adj = ny liste >(); for (int i = 0; i < V; i++) { adj.Add(new List ()); } foreach(Liste i i kanter) { adj[i[0]].Add(i[1]); } TopologiskSort(adj, V); } }
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Driverkode (() => { // Antal noder const V = 4; // Edges const edges = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Graf repræsenteret som en adjacency liste const adj = Array.from({ length: V }, () => [] for (lad i af kanter) { adj[i[0]] (i[1]); } topologicalSort(adj, V })(); Produktion
Topological sorting of the graph: 3 0 1 2
Tidskompleksitet: O(V+E). Ovenstående algoritme er simpelthen DFS med en ekstra stak. Så tidskompleksitet er det samme som DFS
Hjælpeplads: O(V). Den ekstra plads er nødvendig til stakken
Topologisk sortering ved hjælp af BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Pointer til et array, der indeholder // adjacency lists public: Graph(int V); // Konstruktør void addEdge(int v, int w); // Funktion til at tilføje en kant til grafen void topologicalSort(); // udskriver en topologisk sort af // hele grafen }; Graph::Graph(int V) { this->V = V; adj = ny liste [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Tilføj w til vs liste. } // Funktion til at udføre Topological Sort void Graph::topologicalSort() { // Opret en vektor til at gemme i-grad af alle toppunkter vektor in_degree(V, 0); // Gå gennem tilgrænsende lister for at udfylde_grad af // hjørnepunkter for (int v = 0; v < V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; for (int i = 0; i < V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_ordre; // En efter en dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent bliver 0 mens (!q.empty()) { // Udtræk foran i køen (eller udfør dequeue) // og føj det til topologisk rækkefølge int u = q.front(); q.pop(); top_order.push_back(u); // Iterer gennem alle dens tilstødende noder // af udeladt node u og sænk deres in-grad // med 1 liste ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Hvis in-degree bliver nul, føj det til køen hvis (--in_degree[*itr) ] == 0) q.push(*itr); tælle++; } // Tjek om der var en cyklus hvis (tæl != V) { cout < < 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout < < i < < ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout < < 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; } Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Adjacency list // repræsentation af // grafen // Constructor Graph(int V) { this.V = V; adj = ny ArrayList[V]; for (int i = 0; i < V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = new LinkedList(); for (int i = 0; i < V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // En efter en dequeue vertices fra køen og // sæt tilstødende vertices, hvis in-degree af // adjacent bliver 0 mens (!q.isEmpty()) { // Udtræk forsiden af køen og tilføj det til // topologisk rækkefølge int u = q.poll(); topOrder.add(u); tælle++; // Iterer gennem alle dens tilstødende noder af // dequeued node u og reducer deres in-degree // med 1 for (int w : adj[u]) { // Hvis in-degree bliver nul, føj det til // køen if (-inDegree[w] == 0) q.add(w); } } // Tjek om der var en cyklus if (tæl != V) { System.out.println('Graf indeholder cyklus'); Vend tilbage; } // Udskriv topologisk rækkefølge for (int i : topOrder) System.out.print(i + ' '); } } // Driver code public class Main { public static void main(String[] args) { // Opret en graf givet i ovenstående diagram Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Følgende er en topologisk sortering af den givne graf'); g.topologicalSort(); } } Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort() JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh Produktion
Following is a Topological Sort of the given graph 4 5 2 0 3 1
Tidskompleksitet:
Tidskompleksiteten for at konstruere grafen er O(V + E), hvor V er antallet af hjørner og E er antallet af kanter.
Tidskompleksiteten for at udføre topologisk sortering ved hjælp af BFS er også O(V + E), hvor V er antallet af hjørner og E er antallet af kanter. Dette skyldes, at hvert toppunkt og hver kant besøges én gang under BFS-gennemgangen.
Rumkompleksitet:
Rumkompleksiteten for lagring af grafen ved hjælp af en tilgrænsende liste er O(V + E), hvor V er antallet af hjørner og E er antallet af kanter.
Yderligere plads bruges til at gemme den in-grad af hjørner, som kræver O(V) plads.
En kø bruges til BFS-traversal, som højst kan indeholde V-spidser. Pladskompleksiteten for køen er således O(V).
Overordnet set er rumkompleksiteten af algoritmen O(V + E) på grund af lagringen af grafen, in-degree array og køen.
Sammenfattende er tidskompleksiteten af den leverede implementering O(V + E), og rumkompleksiteten er også O(V + E).
Bemærk: Her kan vi også bruge et array i stedet for stakken. Hvis arrayet bruges, så udskriv elementerne i omvendt rækkefølge for at få den topologiske sortering.
Fordele ved topologisk sortering:
- Hjælper med at planlægge opgaver eller begivenheder baseret på afhængigheder.
- Registrerer cyklusser i en rettet graf.
- Effektiv til at løse problemer med prioritetsbegrænsninger.
Ulemper ved topologisk sortering:
- Gælder kun for rettede acykliske grafer (DAG'er), ikke egnet til cykliske grafer.
- Er muligvis ikke unik, der kan eksistere flere gyldige topologiske rækkefølger.
- Ineffektiv til store grafer med mange noder og kanter.
Anvendelser af topologisk sort:
- Opgaveplanlægning og projektledelse.
- Afhængighedsløsning i pakkehåndteringssystemer.
- Bestemmelse af rækkefølgen af kompilering i softwarebyggesystemer.
- Deadlock-detektering i operativsystemer.
- Kursusplanlægning på universiteter.
Relaterede artikler:
- Kahns algoritme for topologisk sortering
- Alle topologiske sorter af en rettet acyklisk graf