Max Heap i Java

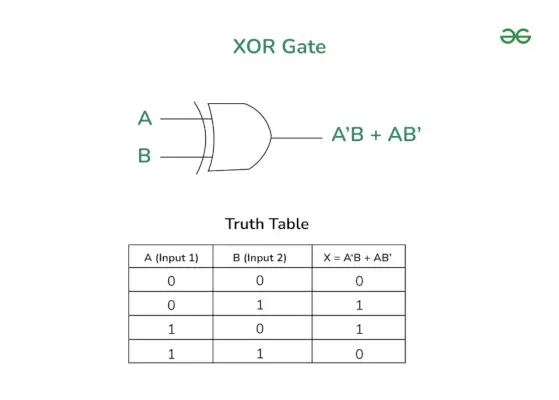
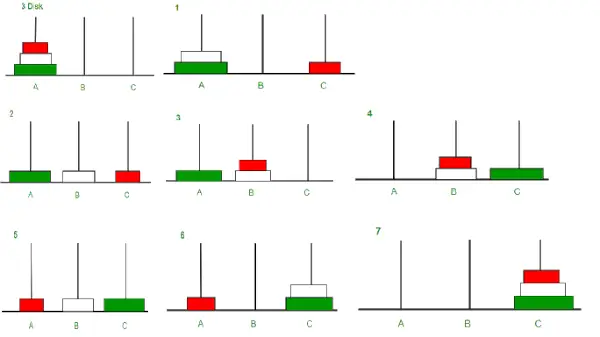
EN max-bunke er et komplet binært træ, hvor værdien i hver intern node er større end eller lig med værdierne i den pågældende nodes børn. At kortlægge elementerne i en heap til et array er trivielt: Hvis en node er lagret et indeks k, så lagres dens venstre underordnede ved indeks 2k + 1 og dets højre underordnede ved indeks 2k + 2.
Illustration: Max Heap

Hvordan er Max Heap repræsenteret?
A-Max Heap er et komplet binært træ. A-Max heap er typisk repræsenteret som et array. Rodelementet vil være ved Arr[0]. Nedenstående tabel viser indekser for andre noder for ith node, dvs. Arr[i]:
Arr[(i-1)/2] Returnerer den overordnede node.
Arr[(2*i)+1] Returnerer den venstre underordnede node.
Arr[(2*i)+2] Returnerer den rigtige underordnede node.
Operationer på Max Heap er som følger:
- getMax(): Det returnerer rodelementet af Max Heap. Tidskompleksiteten af denne operation er O(1) .
- extractMax(): Fjerner det maksimale element fra MaxHeap . Tidskompleksiteten af denne operation er O(Log n) da denne operation skal vedligeholde heap-egenskaben ved at kalde heapify() metode efter at have fjernet roden.
- indsæt(): Indsættelse af en ny nøgle tager O(Log n) tid. Vi tilføjer en ny nøgle for enden af træet. Hvis den nye nøgle er mindre end dens forælder, behøver vi ikke at gøre noget. Ellers er vi nødt til at krydse op for at reparere den krænkede bunkeejendom.
Bemærk: I nedenstående implementering foretager vi indeksering fra indeks 1 for at forenkle implementeringen.
Metoder:
Der er 2 metoder, hvormed vi kan nå det anførte mål:
- Grundlæggende tilgang ved at skabe maxHeapify() metode
- Ved brug af Collections.reverseOrder() metode via biblioteksfunktioner
Metode 1: Grundlæggende tilgang ved at skabe maxHeapify() metode
Vi vil oprette en metode, der antager, at venstre og højre undertræ allerede er ophobet, vi behøver kun at rette roden.
Eksempel
Java
// Java program to implement Max Heap> // Main class> public> class> MaxHeap {> > private> int> [] Heap;> > private> int> size;> > private> int> maxsize;> > // Constructor to initialize an> > // empty max heap with given maximum> > // capacity> > public> MaxHeap(> int> maxsize)> > {> > // This keyword refers to current instance itself> > this> .maxsize = maxsize;> > this> .size => 0> ;> > Heap => new> int> [> this> .maxsize];> > }> > // Method 1> > // Returning position of parent> > private> int> parent(> int> pos) {> return> (pos -> 1> ) /> 2> ; }> > // Method 2> > // Returning left children> > private> int> leftChild(> int> pos) {> return> (> 2> * pos) +> 1> ; }> > // Method 3> > // Returning right children> > private> int> rightChild(> int> pos)> > {> > return> (> 2> * pos) +> 2> ;> > }> > // Method 4> > // Returning true if given node is leaf> > private> boolean> isLeaf(> int> pos)> > {> > if> (pos>(størrelse /> 2> ) && pos <= size) {> > return> true> ;> > }> > return> false> ;> > }> > // Method 5> > // Swapping nodes> > private> void> swap(> int> fpos,> int> spos)> > {> > int> tmp;> > tmp = Heap[fpos];> > Heap[fpos] = Heap[spos];> > Heap[spos] = tmp;> > }> > // Method 6> > // Recursive function to max heapify given subtree> > private> void> maxHeapify(> int> pos)> > {> > if> (isLeaf(pos))> > return> ;> > if> (Heap[pos] || Heap[pos] if (Heap[leftChild(pos)]>Heap[rightChild(pos)]) { swap(pos, leftChild(pos)); maxHeapify(venstreBarn(pos)); } andet { swap(pos, rightChild(pos)); maxHeapify(rightChild(pos)); } } } // Metode 7 // Indsætter et nyt element til max heap public void insert(int element) { Heap[size] = element; // Kør op og fix krænket egenskab int strøm = størrelse; while (Heap[current]> Heap[parent(current)]) { swap(current, parent(current)); nuværende = forælder(aktuel); } størrelse++; } // Metode 8 // For at vise heap public void print() { for (int i = 0; i 2; i++) { System.out.print('Parent Node : ' + Heap[i]); if (venstreBarn(i) // hvis barnet er uden for bunden // af arrayet System.out.print(' Venstre Child-knudepunkt: ' + Heap[venstreBarn(i)]); if (højreBarn(i) ) // det rigtige underordnede indeks må ikke // være uden for indekset for arrayet System.out.print(' Right Child Node: ' + System.out.println() ; // for new line } } // Metode 9 // Fjern et element fra max heap public int extractMax() { int popped = Heap[0] = maxHeapify(0) ; return poppet; } // Metode 10 // hoveddrivermetode public static void main(String[] arg) { // Vis besked for bedre læsbarhed System.out.println('MaxHeap er '); = new MaxHeap(15); // Indsætning af noder maxHeap.insert(3); maxHeap.insert(19); maxHeap.insert(22); værdi i heap System.out.println('Maksimal værdi er ' + maxHeap.extractMax()); } }> |
Produktion
The Max Heap is Parent Node : 84 Left Child Node: 22 Right Child Node: 19 Parent Node : 22 Left Child Node: 17 Right Child Node: 10 Parent Node : 19 Left Child Node: 5 Right Child Node: 6 Parent Node : 17 Left Child Node: 3 Right Child Node: 9 The max val is 84
Metode 2: Brug af metoden Collections.reverseOrder() via biblioteksfunktioner
Vi bruger PriorityQueue-klassen til at implementere Heaps i Java. Min Heap er som standard implementeret af denne klasse. For at implementere Max Heap bruger vi Collections.reverseOrder() metoden.
Eksempel
Java
// Java program to demonstrate working> // of PriorityQueue as a Max Heap> // Using Collections.reverseOrder() method> // Importing all utility classes> import> java.util.*;> // Main class> class> GFG {> > // Main driver method> > public> static> void> main(String args[])> > {> > // Creating empty priority queue> > PriorityQueue pQueue> > => new> PriorityQueue(> > Collections.reverseOrder());> > // Adding items to our priority queue> > // using add() method> > pQueue.add(> 10> );> > pQueue.add(> 30> );> > pQueue.add(> 20> );> > pQueue.add(> 400> );> > // Printing the most priority element> > System.out.println(> 'Head value using peek function:'> > + pQueue.peek());> > // Printing all elements> > System.out.println(> 'The queue elements:'> );> > Iterator itr = pQueue.iterator();> > while> (itr.hasNext())> > System.out.println(itr.next());> > // Removing the top priority element (or head) and> > // printing the modified pQueue using poll()> > pQueue.poll();> > System.out.println(> 'After removing an element '> > +> 'with poll function:'> );> > Iterator itr2 = pQueue.iterator();> > while> (itr2.hasNext())> > System.out.println(itr2.next());> > // Removing 30 using remove() method> > pQueue.remove(> 30> );> > System.out.println(> 'after removing 30 with'> > +> ' remove function:'> );> > Iterator itr3 = pQueue.iterator();> > while> (itr3.hasNext())> > System.out.println(itr3.next());> > // Check if an element is present using contains()> > boolean> b = pQueue.contains(> 20> );> > System.out.println(> 'Priority queue contains 20 '> > +> 'or not?: '> + b);> > // Getting objects from the queue using toArray()> > // in an array and print the array> > Object[] arr = pQueue.toArray();> > System.out.println(> 'Value in array: '> );> > for> (> int> i => 0> ; i System.out.println('Value: ' + arr[i].toString()); } }> |
Produktion
Head value using peek function:400 The queue elements: 400 30 20 10 After removing an element with poll function: 30 10 20 after removing 30 with remove function: 20 10 Priority queue contains 20 or not?: true Value in array: Value: 20 Value: 10