Lær DSA med Python | Python-datastrukturer og algoritmer

Denne tutorial er en begyndervenlig guide til lære datastrukturer og algoritmer ved hjælp af Python. I denne artikel vil vi diskutere de indbyggede datastrukturer såsom lister, tupler, ordbøger osv. og nogle brugerdefinerede datastrukturer som f.eks. sammenkædede lister , træer , grafer , etc, og traversering samt søge- og sorteringsalgoritmer ved hjælp af gode og velforklarede eksempler og øvespørgsmål.

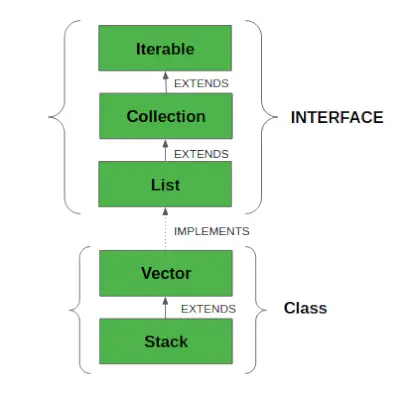
Lister
Python lister er ordnede samlinger af data ligesom arrays i andre programmeringssprog. Det tillader forskellige typer elementer på listen. Implementeringen af Python List ligner Vectors i C++ eller ArrayList i JAVA. Den dyre operation er at indsætte eller slette elementet fra begyndelsen af listen, da alle elementer skal flyttes. Indsættelse og sletning i slutningen af listen kan også blive dyrt i det tilfælde, hvor den forhåndstildelte hukommelse bliver fuld.
Eksempel: Oprettelse af Python-liste
Python3 List = [1, 2, 3, 'GFG', 2.3] print(List)
Produktion
[1, 2, 3, 'GFG', 2.3]
Listeelementer kan tilgås af det tildelte indeks. I python-startindekset på listen er en sekvens 0, og slutindekset er (hvis N elementer er der) N-1.

Eksempel: Python List Operations
Python3 # Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) Produktion
List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks
Tuple
Python-tupler ligner lister, men Tuples er uforanderlig i naturen, dvs. når den først er skabt, kan den ikke ændres. Ligesom en liste kan en Tuple også indeholde elementer af forskellige typer.
I Python oprettes tuples ved at placere en sekvens af værdier adskilt af 'komma' med eller uden brug af parenteser til gruppering af datasekvensen.
Bemærk: For at lave en tuple af et element skal der være et efterfølgende komma. For eksempel vil (8,) skabe en tupel, der indeholder 8 som element.
Eksempel: Python Tuple Operations
Python3 # Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) Produktion
Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 Sæt
Python sæt er en foranderlig samling af data, der ikke tillader nogen duplikering. Sæt bruges grundlæggende til at inkludere medlemskabstest og eliminering af duplikerede poster. Datastrukturen brugt i dette er Hashing, en populær teknik til at udføre indsættelse, sletning og gennemgang i O(1) i gennemsnit.
Hvis flere værdier er til stede på den samme indeksposition, føjes værdien til denne indeksposition for at danne en sammenkædet liste. I implementeres CPython-sæt ved hjælp af en ordbog med dummy-variabler, hvor nøglevæsener medlemmerne sætter med større optimeringer til tidskompleksiteten.
Sæt implementering:

Sæt med talrige operationer på en enkelt HashTable:

Eksempel: Python Set Operations
Python3 # Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) Produktion
Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True Frosne sæt
Frosne sæt i Python er uforanderlige objekter, der kun understøtter metoder og operatører, der producerer et resultat uden at påvirke det eller de frosne sæt, som de anvendes på. Mens elementer i et sæt kan ændres til enhver tid, forbliver elementer i det frosne sæt de samme efter oprettelsen.
Eksempel: Python Frozen sæt
Python3 # Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') Produktion
Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) Snor
Python strenge er den uforanderlige række af bytes, der repræsenterer Unicode-tegn. Python har ikke en karakterdatatype, et enkelt tegn er blot en streng med en længde på 1.
Bemærk: Da strenge er uforanderlige, vil ændring af en streng resultere i oprettelse af en ny kopi.

Eksempel: Python Strings Operations
Python3 String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) Produktion
Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s
Ordbog
Python ordbog er en uordnet samling af data, der gemmer data i formatet nøgle:værdi par. Det er ligesom hashtabeller på ethvert andet sprog med tidskompleksiteten O(1). Indeksering af Python Dictionary sker ved hjælp af nøgler. Disse er af enhver hashbar type, dvs. et objekt, hvis objekt aldrig kan ændre sig som strenge, tal, tupler osv. Vi kan oprette en ordbog ved at bruge krøllede klammeparenteser ({}) eller ordbogsforståelse.
Eksempel: Python Dictionary Operations
Python3 # Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) Produktion
Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} Matrix
En matrix er et 2D-array, hvor hvert element er af strengt taget samme størrelse. For at oprette en matrix vil vi bruge NumPy pakke .
Eksempel: Python NumPy Matrix Operations
Python3 import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) Produktion
[[ 1 2 3 4] [ 4 55 1 2] [ 8 3 20 19] [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4] [ 4 55 1 2] [ 8 3 20 19] [11 2 22 21] [ 1 15 13 11]] Deleting Element [[ 1 2 3 4] [ 8 3 20 19] [11 2 22 21] [ 1 15 13 11]]
Bytearray
Python Bytearray giver en foranderlig sekvens af heltal i området 0 <= x < 256.
Eksempel: Python Bytearray Operations
Python3 # Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) Produktion
Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')
Linket liste
EN linket liste er en lineær datastruktur, hvor elementerne ikke er lagret på sammenhængende hukommelsesplaceringer. Elementerne i en linket liste er linket ved hjælp af pointere som vist på billedet nedenfor:

En sammenkædet liste er repræsenteret af en pegepind til den første knude på den sammenkædede liste. Den første knude kaldes hovedet. Hvis den linkede liste er tom, så er værdien af hovedet NULL. Hver node i en liste består af mindst to dele:
- Data
- Pointer (eller reference) til næste knude
Eksempel: Definition af linket liste i Python
Python3 # Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None
Lad os oprette en simpel linket liste med 3 noder.
Python3 # A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) ''' Three nodes have been created. We have references to these three blocks as head, second and third llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | None | | 2 | None | | 3 | None | +----+------+ +----+------+ +----+------+ ''' llist.head.next = second; # Link first node with second ''' Now next of first Node refers to second. So they both are linked. llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | null | | 3 | null | +----+------+ +----+------+ +----+------+ ''' second.next = tredje ; # Forbind anden node med den tredje node ''' Nu refererer næste af anden node til tredje. Så alle tre noder er forbundet. llist.head anden tredje | | | | | | +----+------+ +----+-----+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null | +----+------+ +----+------+ +----+------+ '''
Linket listegennemgang
I det forrige program har vi lavet en simpel sammenkædet liste med tre noder. Lad os krydse den oprettede liste og udskrive dataene for hver node. For gennemgang, lad os skrive en generel funktion printList(), der udskriver en given liste.
Python3 # A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()
Produktion
1 2 3
Flere artikler om Linked List
- Indsættelse af linket liste
- Sletning af linket liste (sletning af en given nøgle)
- Linket listesletning (sletning af en nøgle på en given position)
- Find længden af en sammenkædet liste (iterativ og rekursiv)
- Søg efter et element i en sammenkædet liste (iterativ og rekursiv)
- N. knude fra slutningen af en sammenkædet liste
- Vend en sammenkædet liste

Funktionerne forbundet med stack er:
- tomme() – Returnerer, om stakken er tom – Tidskompleksitet: O(1)
- størrelse() – Returnerer stakkens størrelse – Tidskompleksitet: O(1)
- top() – Returnerer en reference til det øverste element i stakken – Tidskompleksitet: O(1)
- push(a) – Indsætter elementet 'a' i toppen af stakken - Tidskompleksitet: O(1)
- pop() – Sletter det øverste element i stakken – Tidskompleksitet: O(1)
stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty Produktion
Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []
Flere artikler om Stack
- Infix til Postfix-konvertering ved hjælp af stak
- Præfiks til Infix-konvertering
- Præfiks til Postfix-konvertering
- Postfix til præfikskonvertering
- Postfix til Infix
- Tjek for afbalancerede parenteser i et udtryk
- Evaluering af Postfix-udtryk
Som en stak kø er en lineær datastruktur, der gemmer elementer på en First In First Out (FIFO) måde. Med en kø fjernes det mindst nyligt tilføjede element først. Et godt eksempel på køen er enhver kø af forbrugere til en ressource, hvor den forbruger, der kom først, bliver serveret først.

Operationer forbundet med kø er:
- Kø: Tilføjer et element til køen. Hvis køen er fuld, siges det at være en overløbstilstand – Tidskompleksitet: O(1)
- Derfor: Fjerner en vare fra køen. Elementerne poppes i samme rækkefølge, som de skubbes. Hvis køen er tom, siges det at være en underløbstilstand – Tidskompleksitet: O(1)
- Foran: Få det forreste element fra køen – Tidskompleksitet: O(1)
- Bag: Hent den sidste vare fra køen – Tidskompleksitet: O(1)
# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty Produktion
Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []
Flere artikler om kø
- Implementer kø ved hjælp af stakke
- Implementer stak ved hjælp af køer
- Implementer en stak ved hjælp af enkelt kø
Prioritetskø
Prioriterede køer er abstrakte datastrukturer, hvor hver data/værdi i køen har en vis prioritet. For eksempel hos flyselskaber ankommer bagage med titlen Business eller First-class tidligere end resten. Priority Queue er en udvidelse af køen med følgende egenskaber.
- Et element med høj prioritet sættes ud af kø før et element med lav prioritet.
- Hvis to elementer har samme prioritet, serveres de i henhold til deres rækkefølge i køen.
# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] return item undtagen IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) mens ikke myQueue.isEmpty(): print(myQueue.delete())
Produktion
12 1 14 7 14 12 7 1
Dynge
heapq-modul i Python leverer heap-datastrukturen, der hovedsageligt bruges til at repræsentere en prioritetskø. Egenskaben ved denne datastruktur er, at den altid giver det mindste element (min heap), når elementet poppes. Når elementer skubbes eller poppes, bibeholdes bunkestrukturen. Heap[0]-elementet returnerer også det mindste element hver gang. Det understøtter udtrækning og indsættelse af det mindste element i O(log n) gange.
Generelt kan heaps være af to typer:
- Max-Heap: I en Max-Heap skal nøglen, der er til stede ved rodknuden, være størst blandt de nøgler, der er til stede på alle dens børn. Den samme egenskab skal være rekursivt sand for alle undertræer i det binære træ.
- Min-bunke: I en Min-Heap skal nøglen, der er til stede ved rodknuden, være minimum blandt nøglerne, der er til stede på alle dens børn. Den samme egenskab skal være rekursivt sand for alle undertræer i det binære træ.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) Produktion
The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1
Flere artikler om Heap
- Binær bunke
- K'th største element i et array
- K'th mindste/største element i usorteret array
- Sorter et næsten sorteret array
- K-te Største Sum Sammenhængende Subarray
- Minimumsummen af to tal dannet af cifre i en matrix
Et træ er en hierarkisk datastruktur, der ser ud som nedenstående figur –
tree ---- j <-- root / f k / a h z <-- leaves
Træets øverste knude kaldes roden, mens de nederste knudepunkter eller knuderne uden børn kaldes bladknuderne. De noder, der er direkte under en node, kaldes dens børn, og de noder, der er direkte over noget, kaldes dens forælder.
EN binært træ er et træ, hvis elementer kan få næsten to børn. Da hvert element i et binært træ kun kan have 2 børn, kalder vi dem typisk venstre og højre børn. En binær træknude indeholder følgende dele.
- Data
- Viser til venstre barn
- Pointer til det rigtige barn
Eksempel: Definition af nodeklasse
Python3 # A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key
Lad os nu oprette et træ med 4 noder i Python. Lad os antage, at træstrukturen ser ud som nedenfor -
tree ---- 1 <-- root / 2 3 / 4
Eksempel: Tilføjelse af data til træet
Python3 # Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement 1 / None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1 1 / 2 3 / / None None None None''' root.left.left = Node(4); '''4 becomes left child of 2 1 / 2 3 / / 4 None None None / None None'''
Trægennemgang
Træer kan krydses på forskellige måder. Følgende er de almindeligt anvendte måder at krydse træer på. Lad os overveje nedenstående træ -
tree ---- 1 <-- root / 2 3 / 4 5
Dybde første gennemløb:
- I rækkefølge (venstre, rod, højre): 4 2 5 1 3
- Forudbestil (rod, venstre, højre): 1 2 4 5 3
- Postordre (venstre, højre, rod): 4 5 2 3 1
Algoritme rækkefølge (træ)
- Gå gennem det venstre undertræ, dvs. kald Inorder (venstre-undertræ)
- Besøg roden.
- Gå gennem det højre undertræ, dvs. kald Inorder (højre-undertræ)
Algoritme forudbestilling (træ)
- Besøg roden.
- Gå gennem det venstre undertræ, dvs. kald Preorder (venstre-undertræ)
- Gå gennem det højre undertræ, dvs. kald Preorder (højre-undertræ)
Algoritme Postordre (træ)
- Gå gennem det venstre undertræ, dvs. kald Postorder (venstre-undertræ)
- Gå gennem det højre undertræ, dvs. kald Postorder (højre-undertræ)
- Besøg roden.
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) Produktion
Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1
Tidskompleksitet – O(n)
Breadth-First eller Level Order Traversal
Niveauordregennemgang af et træ er bredde-første traversering for træet. Niveauordregennemgangen af ovenstående træ er 1 2 3 4 5.
For hver node besøges først noden, og derefter sættes dens underordnede noder i en FIFO-kø. Nedenfor er algoritmen for det samme –
- Opret en tom kø q
- temp_node = root /*start fra root*/
- Loop mens temp_node ikke er NULL
- udskriv temp_node->data.
- Sæt temp_nodes børn i kø (først venstre og derefter højre børn) til q
- Sæt en node i kø fra q
# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Udskriv forrest i køen, og # fjern det fra køudskrift (kø[0].data) node = queue.pop(0) # Sæt venstre underord i kø, hvis node.left ikke er Ingen: queue.append(node.left ) # Enqueue right child if node.right ikke er Ingen: queue.append(node.right) # Driver Program til at teste ovenstående funktion root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('Level Order Traversal af binært træ er -') printLevelOrder(root) Produktion
Level Order Traversal of binary tree is - 1 2 3 4 5
Tidskompleksitet: O(n)
Flere artikler om Binary Tree
- Indsættelse i et binært træ
- Sletning i et binært træ
- Inorder trægennemgang uden rekursion
- Bestil Tree Traversal uden rekursion og uden stak!
- Udskriv Postorder-gennemgang fra givne Inorder- og Preorder-gennemgange
- Find postorder traversal af BST fra preorder traversal
Binært søgetræ er en nodebaseret binær trædatastruktur, der har følgende egenskaber:
- Det venstre undertræ af en node indeholder kun noder med nøgler, der er mindre end nodens nøgle.
- Det højre undertræ af en node indeholder kun noder med nøgler, der er større end nodens nøgle.
- Det venstre og højre undertræ skal hver også være et binært søgetræ.

Ovenstående egenskaber for det binære søgetræ giver en rækkefølge blandt nøgler, så operationer som søgning, minimum og maksimum kan udføres hurtigt. Hvis der ikke er nogen ordre, skal vi muligvis sammenligne hver nøgle for at søge efter en given nøgle.
Søgeelement
- Start fra roden.
- Sammenlign søgeelementet med root, hvis mindre end root, så recurse for venstre, ellers recurse for højre.
- Hvis elementet, der skal søges, findes nogen steder, returneres sand, ellers returneres falsk.
# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)
Indsættelse af nøgle
- Start fra roden.
- Sammenlign indsættelseselementet med rod, hvis mindre end rod, så recurse for venstre, ellers recurse for højre.
- Når du har nået enden, skal du bare indsætte den node til venstre (hvis mindre end den nuværende) ellers til højre.
# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # / # 30 70 # / / # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)
Produktion
20 30 40 50 60 70 80
Flere artikler om binært søgetræ
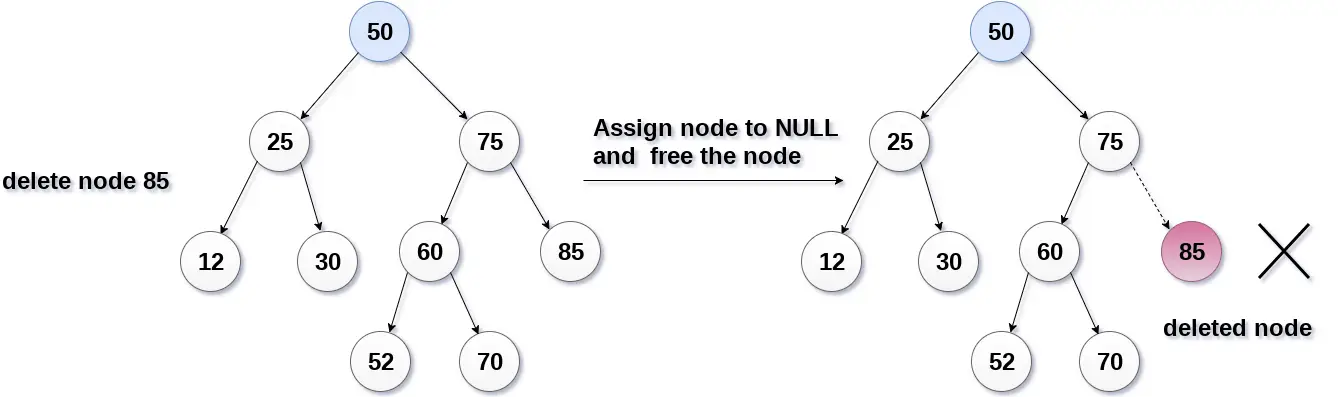
- Binært søgetræ – Slet nøgle
- Konstruer BST ud fra givet forudbestillingsgennemgang | Sæt 1
- Konvertering af binært træ til binært søgetræ
- Find noden med minimumsværdi i et binært søgetræ
- Et program til at kontrollere, om et binært træ er BST eller ej
EN kurve er en ikke-lineær datastruktur bestående af noder og kanter. Noderne omtales nogle gange også som hjørner, og kanterne er linjer eller buer, der forbinder to vilkårlige noder i grafen. Mere formelt kan en graf defineres som en graf bestående af et endeligt sæt af knudepunkter (eller noder) og et sæt kanter, der forbinder et par knudepunkter.

I ovenstående graf er sættet af hjørner V = {0,1,2,3,4} og sættet af kanter E = {01, 12, 23, 34, 04, 14, 13}. De følgende to er de mest brugte repræsentationer af en graf.
- Adjacency Matrix
- Tilgrænsende liste
Adjacency Matrix
Adjacency Matrix er et 2D-array af størrelse V x V, hvor V er antallet af hjørner i en graf. Lad 2D-arrayet være adj[][], et slot adj[i][j] = 1 indikerer, at der er en kant fra toppunkt i til toppunkt j. Adjacency-matrixen for en urettet graf er altid symmetrisk. Adjacency Matrix bruges også til at repræsentere vægtede grafer. Hvis adj[i][j] = w, så er der en kant fra toppunkt i til toppunkt j med vægt w.
Python3 # A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) Produktion
Grafens hjørner
['a', 'b', 'c', 'd', 'e', 'f']
Kanter af graf
[('a', 'c', 20), ('a', 'e', 10), ('b', 'c', 30), ('b', 'e', 40), ( 'c', 'a', 20), ('c', 'b', 30), ('d', 'e', 50), ('e', 'a', 10), ('e ', 'b', 40), ('e', 'd', 50), ('e', 'f', 60), ('f', 'e', 60)]
Adjacency Matrix of Graph
[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]
Tilgrænsende liste
Der bruges en række lister. Størrelsen af arrayet er lig med antallet af hjørner. Lad arrayet være et array[]. En indgangsmatrix[i] repræsenterer listen over toppunkter, der støder op til det ith-punkt. Denne repræsentation kan også bruges til at repræsentere en vægtet graf. Vægten af kanter kan repræsenteres som lister over par. Følgende er en gengivelse af nabolisten af ovenstående graf.

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print('
') # Driverprogram til ovenstående grafklasse hvis __navn__ == '__main__' : V = 5 graf = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() Produktion
Adjacency list of vertex 0 head ->4 -> 1 Adjacency liste over toppunkt 1 hoved -> 4 -> 3 -> 2 -> 0 Adjacency liste over toppunkt 2 hoved -> 3 -> 1 Adjacency liste af toppunkt 3 hoved -> 4 -> 2 -> 1 Adjacency liste over toppunkt 4 hoved -> 3 -> 1 -> 0
Grafgennemgang
Breadth-First Search eller BFS
Bredth-First Traversal for en graf ligner Breadth-First Traversal af et træ. Den eneste fangst her er, i modsætning til træer, kan grafer indeholde cyklusser, så vi kan komme til den samme knude igen. For at undgå at behandle en node mere end én gang, bruger vi et boolesk besøgt array. For nemheds skyld antages det, at alle toppunkter er tilgængelige fra startpunktet.
For eksempel, i den følgende graf, starter vi traversering fra toppunkt 2. Når vi kommer til toppunkt 0, leder vi efter alle tilstødende toppunkter af det. 2 er også et tilstødende toppunkt på 0. Hvis vi ikke markerer besøgte toppunkter, vil 2 blive behandlet igen, og det bliver en ikke-afsluttende proces. En Breadth-First Traversal af følgende graf er 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) Produktion
Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1
Tidskompleksitet: O(V+E) hvor V er antallet af hjørner i grafen og E er antallet af kanter i grafen.
Depth First Search eller DFS
Dybde første gennemløb for en graf svarer til Depth First Traversal af et træ. Den eneste fangst her er, i modsætning til træer, grafer kan indeholde cyklusser, en node kan besøges to gange. For at undgå at behandle en node mere end én gang skal du bruge en boolsk besøgt matrix.
Algoritme:
- Opret en rekursiv funktion, der tager indekset for noden og et besøgt array.
- Marker den aktuelle node som besøgt, og udskriv noden.
- Gå gennem alle tilstødende og umarkerede noder og kald den rekursive funktion med indekset for den tilstødende node.
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) Produktion
Following is DFS from (starting from vertex 2) 2 0 1 3
Flere artikler om graf
- Tegn grafiske repræsentationer ved hjælp af sæt og hash
- Find Mother Vertex i en graf
- Iterativ dybde først søgning
- Tæl antallet af noder på et givet niveau i et træ ved hjælp af BFS
- Tæl alle mulige veje mellem to hjørner
Processen, hvor en funktion kalder sig selv direkte eller indirekte, kaldes rekursion, og den tilsvarende funktion kaldes en rekursiv funktion . Ved at bruge de rekursive algoritmer kan visse problemer løses ganske nemt. Eksempler på sådanne problemer er Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph osv.
Hvad er grundtilstanden ved rekursion?
I det rekursive program gives løsningen på basissagen, og løsningen af det større problem udtrykkes i form af mindre problemer.
def fact(n): # base case if (n <= 1) return 1 else return n*fact(n-1)
I ovenstående eksempel er basistilfælde for n <= 1 defineret, og større værdi af tal kan løses ved at konvertere til mindre et, indtil grundtilfælde er nået.
Hvordan allokeres hukommelse til forskellige funktionskald i rekursion?
Når en funktion kaldes fra main(), allokeres hukommelsen til den på stakken. En rekursiv funktion kalder sig selv, hukommelsen for en kaldt funktion allokeres oven på hukommelsen allokeret til den kaldende funktion, og en anden kopi af lokale variabler oprettes for hvert funktionskald. Når basistilfældet er nået, returnerer funktionen sin værdi til den funktion, som den kaldes af, og hukommelsen de-allokeres, og processen fortsætter.
Lad os tage eksemplet på, hvordan rekursion virker ved at tage en simpel funktion.
Python3 # A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)
Produktion
3 2 1 1 2 3
Hukommelsesstakken er vist i diagrammet nedenfor.

Flere artikler om rekursion
- Rekursion
- Rekursion i Python
- Øvelsesspørgsmål til rekursion | Sæt 1
- Øvelsesspørgsmål til rekursion | Sæt 2
- Øvelsesspørgsmål til rekursion | Sæt 3
- Øvelsesspørgsmål til rekursion | Sæt 4
- Øvelsesspørgsmål til rekursion | Sæt 5
- Øvelsesspørgsmål til rekursion | Sæt 6
- Øvelsesspørgsmål til rekursion | Sæt 7
>>> mere
Dynamisk programmering
Dynamisk programmering er hovedsageligt en optimering over almindelig rekursion. Uanset hvor vi ser en rekursiv løsning, der har gentagne opkald til samme input, kan vi optimere den ved hjælp af dynamisk programmering. Ideen er simpelthen at gemme resultaterne af delproblemer, så vi ikke behøver at genberegne dem, når det er nødvendigt senere. Denne simple optimering reducerer tidskompleksitet fra eksponentiel til polynomium. For eksempel, hvis vi skriver simpel rekursiv løsning til Fibonacci-tal, får vi eksponentiel tidskompleksitet, og hvis vi optimerer den ved at gemme løsninger af delproblemer, reduceres tidskompleksiteten til lineær.

Tabulation vs Memoization
Der er to forskellige måder at gemme værdierne på, så værdierne for et delproblem kan genbruges. Her vil vi diskutere to mønstre til løsning af dynamisk programmeringsproblem (DP):
- Tabulation: Bunden i vejret
- Memoisering: Oppefra og ned
Tabulation
Som navnet i sig selv antyder, starter du fra bunden og samler svar til toppen. Lad os diskutere med hensyn til statsovergang.
Lad os beskrive en tilstand for vores DP-problem til at være dp[x] med dp[0] som basistilstand og dp[n] som vores destinationstilstand. Så vi skal finde værdien af destinationstilstand, dvs. dp[n].
Hvis vi starter vores overgang fra vores basistilstand, dvs. dp[0] og følger vores tilstandsovergangsforhold for at nå vores destinationstilstand dp[n], kalder vi det Bottom-Up-tilgangen, da det er helt klart, at vi startede vores overgang fra nederste basistilstand og nåede den øverste ønskede tilstand.
Nu, hvorfor kalder vi det tabuleringsmetode?
For at vide dette, lad os først skrive noget kode for at beregne fakultetet af et tal ved hjælp af bottom up-tilgang. Endnu en gang, igen som vores generelle procedure til at løse en DP, definerer vi først en tilstand. I dette tilfælde definerer vi en tilstand som dp[x], hvor dp[x] er at finde faktoren af x.
Nu er det ret indlysende, at dp[x+1] = dp[x] * (x+1)
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1): dp[i] = dp[i-1] * i
Memoisering
Endnu en gang, lad os beskrive det i form af statsovergang. Hvis vi skal finde værdien for en tilstand, sig dp[n] og i stedet for at starte fra basistilstanden, dvs. dp[0], spørger vi vores svar fra de stater, der kan nå destinationstilstanden dp[n] efter tilstandsovergangen forhold, så er det top-down mode hos DP.
Her starter vi vores rejse fra den øverste destinationstilstand og beregner svaret ved at tælle værdierne af tilstande, der kan nå destinationstilstanden, indtil vi når den nederste basistilstand.
Endnu en gang, lad os skrive koden til det faktorielle problem på top-down måde
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x): if (x==0) return 1 if (dp[x]!=-1) return dp[x] return (dp[x] = x * solve(x-1))

Flere artikler om dynamisk programmering
- Optimal underbygningsejendom
- Overlappende underproblemer egenskab
- Fibonacci-tal
- Delmængde med sum delelig med m
- Maksimal Sum Stigende Subsequence
- Længste fælles understreng
Søgealgoritmer
Lineær søgning
- Start fra elementet længst til venstre i arr[] og en efter en sammenlign x med hvert element i arr[]
- Hvis x matcher et element, returneres indekset.
- Hvis x ikke stemmer overens med nogen af elementerne, returneres -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) Produktion
Element is present at index 3
Tidskompleksiteten af ovenstående algoritme er O(n).
For mere information, se Lineær søgning .
Binær søgning
Søg i et sorteret array ved gentagne gange at dele søgeintervallet i to. Begynd med et interval, der dækker hele arrayet. Hvis værdien af søgenøglen er mindre end elementet i midten af intervallet, skal du indsnævre intervallet til den nederste halvdel. Ellers skal du indsnævre den til den øverste halvdel. Kontroller gentagne gange, indtil værdien er fundet, eller intervallet er tomt.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Hvis element er til stede i selve midten, hvis arr[mid] == x: return mid # Hvis element er mindre end mid, så kan # kun være til stede i venstre subarray elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Ellers kan elementet kun være til stede # i højre subarray else: return binarySearch(arr, mid + 1, r, x ) andet: # Element er ikke til stede i arrayet returnerer -1 # Driverkode arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funktionsopkaldsresultat = binærSøg(arr, 0, len(arr)-1 , x) hvis resultat != -1: print ('Element er til stede ved indeks % d' % resultat) else: print ('Element er ikke til stede i array') Produktion
Element is present at index 3
Tidskompleksiteten af ovenstående algoritme er O(log(n)).
For mere information, se Binær søgning .
Sorteringsalgoritmer
Udvalgssortering
Det udvælgelsessortering algoritmen sorterer et array ved gentagne gange at finde minimumselementet (i betragtning af stigende rækkefølge) fra usorteret del og sætte det i begyndelsen. I hver iteration af udvælgelsessortering plukkes minimumselementet (i betragtning af stigende rækkefølge) fra den usorterede subarray og flyttes til den sorterede subarray.
Flowchart over udvælgelsessorten:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Skift det fundne minimumselement med # det første element A[i], A[min_idx] = A[min_idx], A[i] # Driverkode til test over print ('Sorteret array ') for i i området(len(A)): print('%d' %A[i]), Produktion
Sorted array 11 12 22 25 64
Tidskompleksitet: På 2 ), da der er to indlejrede løkker.
Hjælpeplads: O(1)
Boble sortering
Boble sortering er den enkleste sorteringsalgoritme, der fungerer ved gentagne gange at udskifte de tilstødende elementer, hvis de er i forkert rækkefølge.
Illustration:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Driverkode til test over arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Sorteret array er:') for i i området(len(arr)): print ('%d' %arr[i]), Produktion
Sorted array is: 11 12 22 25 34 64 90
Tidskompleksitet: På 2 )
Indsættelsessortering
For at sortere en matrix af størrelse n i stigende rækkefølge ved hjælp af indsættelsessortering :
- Iterér fra arr[1] til arr[n] over arrayet.
- Sammenlign det nuværende element (nøgle) med dets forgænger.
- Hvis nøgleelementet er mindre end dets forgænger, skal du sammenligne det med elementerne før. Flyt de større elementer en position op for at gøre plads til det ombyttede element.
Illustration:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 og tast < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) Produktion
5 6 11 12 13
Tidskompleksitet: På 2 ))
Flet sortering
Ligesom QuickSort, Flet sortering er en Divide and Conquer-algoritme. Det opdeler input-arrayet i to halvdele, kalder sig selv for de to halvdele og flettes derefter de to sorterede halvdele. Merge()-funktionen bruges til at flette to halvdele. Sammenfletningen(arr, l, m, r) er en nøgleproces, der antager, at arr[l..m] og arr[m+1..r] er sorteret og flettes sammen de to sorterede sub-arrays til én.
MergeSort(arr[], l, r) If r>l 1. Find det midterste punkt for at opdele arrayet i to halvdele: midterste m = l+ (r-l)/2 2. Kald fletSortér for første halvdel: Kald fletSortering(arr, l, m) 3. Kald fletSortér for anden halvdel: Kald mergeSort(arr, m+1, r) 4. Flet de to halvdele sorteret i trin 2 og 3: Kald merge(arr, l, m, r)
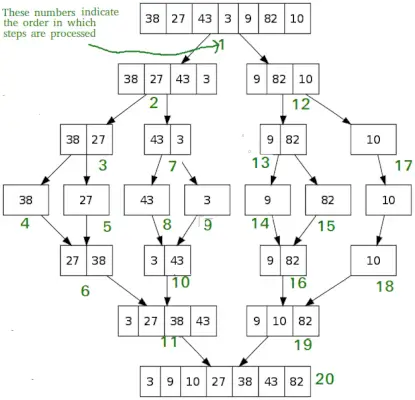
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Find midten af arrayet mid = len(arr)//2 # Opdeling af array-elementerne L = arr[:mid] # i 2 halvdele R = arr[midt:] # Sortering af den første halvdel MergeSort(L) # Sortering af anden halvdel MergeSort(R) i = j = k = 0 # Kopier data til midlertidige arrays L[] og R[] mens i < len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) Produktion
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13
Tidskompleksitet: O(n(logn))
QuickSort
Ligesom Merge Sort, QuickSort er en Divide and Conquer-algoritme. Den vælger et element som pivot og opdeler det givne array omkring det valgte pivot. Der er mange forskellige versioner af quickSort, der vælger pivot på forskellige måder.
Vælg altid det første element som pivot.
- Vælg altid det sidste element som pivot (implementeret nedenfor)
- Vælg et tilfældigt element som pivot.
- Vælg median som pivot.
Nøgleprocessen i quickSort er partition(). Mål for partitioner er, givet et array og et element x af array som pivot, at sætte x i dens korrekte position i sorteret array og sætte alle mindre elementer (mindre end x) før x, og sætte alle større elementer (større end x) efter x. Alt dette skal gøres i lineær tid.
/* low -->Startindeks, høj --> Slutindeks */ quickSort(arr[], lav, høj) { if (low { /* pi er partitioneringsindeks, arr[pi] er nu på det rigtige sted */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Before pi quickSort(arr, pi + 1, high } } 
Opdelingsalgoritme
Der kan være mange måder at gøre partition, følgende pseudo kode anvender metoden angivet i CLRS bog. Logikken er enkel, vi starter fra elementet længst til venstre og holder styr på indekset for mindre (eller lig med) elementer som i. Mens vi krydser, hvis vi finder et mindre element, bytter vi det nuværende element med arr[i]. Ellers ignorerer vi det aktuelle element.
pivot: end -= 1 # Hvis start og slut ikke har krydset hinanden, # skift tallene på start og slut if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') Produktion
Sorted array: [1, 5, 7, 8, 9, 10]
Tidskompleksitet: O(n(logn))
ShellSort
ShellSort er hovedsageligt en variation af Insertion Sort. Ved indsættelsessortering flytter vi elementer kun én position frem. Når et element skal flyttes langt frem, er der mange bevægelser involveret. Ideen med shellSort er at tillade udveksling af fjerne genstande. I shellSort laver vi arrayet h-sorteret til en stor værdi af h. Vi bliver ved med at reducere værdien af h, indtil den bliver 1. En matrix siges at være h-sorteret, hvis alle underlister af hver h th element er sorteret.
Python3 # Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = mellemrum # check arrayet ind fra venstre mod højre # indtil det sidste mulige indeks af j mens j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # nu, vi ser tilbage fra i indeks til venstre # vi bytter værdierne, som er ikke i den rigtige rækkefølge. k = i mens k - gap> -1: hvis arr[k - gap]> arr[k]: arr[k-gap],arr[k] = arr[k],arr[k-gap] k -= 1 mellemrum //= 2 # driver til at kontrollere koden arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) Produktion
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54]
Tidskompleksitet: På 2 ).