INORDER GENNEMGANG AF BINÆRT TRÆ - TECHCODEVIEW.COM

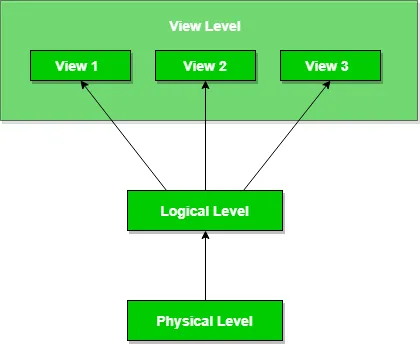
Gennemgang af uorden er defineret som en type trægennemløbsteknik som følger venstre-rod-højre-mønsteret, således at:

Det venstre undertræ krydses først

Derefter krydses rodknuden for det undertræ

Til sidst krydses det højre undertræ

Gennemgang af uorden

Algoritme for Inorder Traversal af binært træ

Algoritmen for gennemløb af uorden er vist som følger:

Inorder (rod):

Følg trin 2 til 4 indtil root != NULL

I rækkefølge (rod -> venstre)

Skriv root -> data

I rækkefølge (rod -> højre)

Slut sløjfe

Hvordan virker Inorder Traversal of Binary Tree?

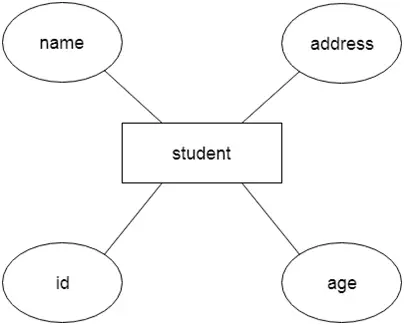
Overvej følgende træ:

Eksempel på binært træ

Hvis vi udfører en uordensgennemgang i dette binære træ, vil gennemgangen være som følger:

Trin 1: Gennemgangen vil gå fra 1 til dets venstre undertræ, dvs. 2, derefter fra 2 til dets venstre undertrærod, dvs. 4. Nu har 4 ikke noget venstre undertræ, så det vil blive besøgt. Den har heller ikke noget ret undertræ. Så ikke mere traversering fra 4

Node 4 er besøgt

Trin 2: Da det venstre undertræ af 2 besøges fuldstændigt, læser det nu data fra node 2, før det flytter til dets højre undertræ.

Node 2 er besøgt

Trin 3: Nu vil det højre undertræ af 2 blive krydset, dvs. flytte til node 5. For node 5 er der ikke noget venstre undertræ, så det bliver besøgt, og derefter kommer gennemgangen tilbage, fordi der ikke er noget højre undertræ af node 5.

Node 5 er besøgt

Trin 4: Som det venstre undertræ af node 1 er, vil selve roden, dvs. node 1 blive besøgt.

Node 1 er besøgt

Trin 5: Venstre undertræ af node 1 og selve noden besøges. Så nu vil det højre undertræ af 1 blive krydset, dvs. flytte til node 3. Da node 3 ikke har noget venstre undertræ, så bliver det besøgt.

Node 3 er besøgt

Trin 6: Det venstre undertræ af node 3 og selve noden besøges. Så gå til det højre undertræ og besøg knudepunkt 6. Nu slutter gennemkørslen, når alle knuderne krydses.

Hele træet krydses

Så rækkefølgen af krydsning af noder er 4 -> 2 -> 5 -> 1 -> 3 -> 6 .

Program til at implementere Inorder Traversal of Binary Tree:

Nedenfor er kodeimplementeringen af inorder-gennemgangen:

C++

// C++ program for inorder traversals> #include> using> namespace> std;> // Structure of a Binary Tree Node> struct> Node {> > int> data;> > struct> Node *left, *right;> > Node(> int> v)> > {> > data = v;> > left = right = NULL;> > }> };> // Function to print inorder traversal> void> printInorder(> struct> Node* node)> {> > if> (node == NULL)> > return> ;> > // First recur on left subtree> > printInorder(node->venstre);> > // Now deal with the node> >

cout ' ';  // Then recur on right subtree  printInorder(node->højre); } // Driverkode int main() { struct Node* root = new Node(1);  root->venstre = ny node(2);  root->right = ny node(3);  root->venstre->venstre = ny node(4);  root->venstre->højre = ny node(5);  root->right->right = new Node(6);  // Funktionskald cout < < 'Inorder traversal of binary tree is: 
';  printInorder(root);  return 0; }>

Java

// Java program for inorder traversals> import> java.util.*;> // Structure of a Binary Tree Node> class> Node {> > int> data;> > Node left, right;> > Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Main class> class> GFG {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > System.out.print(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > Node root => new> Node(> 1> );> > root.left => new> Node(> 2> );> > root.right => new> Node(> 3> );> > root.left.left => new> Node(> 4> );> > root.left.right => new> Node(> 5> );> > root.right.right => new> Node(> 6> );> > // Function call> > System.out.println(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }> // This code is contributed by prasad264>

Python3

# Structure of a Binary Tree Node> class> Node:> > def> __init__(> self> , v):> > self> .data> => v> > self> .left> => None> > self> .right> => None> # Function to print inorder traversal> def> printInorder(node):> > if> node> is> None> :> > return> > # First recur on left subtree> > printInorder(node.left)> > # Now deal with the node> > print> (node.data, end> => ' '> )> > # Then recur on right subtree> > printInorder(node.right)> # Driver code> if> __name__> => => '__main__'> :> > root> => Node(> 1> )> > root.left> => Node(> 2> )> > root.right> => Node(> 3> )> > root.left.left> => Node(> 4> )> > root.left.right> => Node(> 5> )> > root.right.right> => Node(> 6> )> > # Function call> > print> (> 'Inorder traversal of binary tree is:'> )> > printInorder(root)>

C#

// C# program for inorder traversals> using> System;> // Structure of a Binary Tree Node> public> class> Node {> > public> int> data;> > public> Node left, right;> > public> Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Class to store and print inorder traversal> public> class> BinaryTree {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > Console.Write(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> Main()> > {> > Node root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > Console.WriteLine(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }>

Javascript

// JavaScript program for inorder traversals> // Structure of a Binary Tree Node> class Node {> > constructor(v) {> > this> .data = v;> > this> .left => null> ;> > this> .right => null> ;> > }> }> // Function to print inorder traversal> function> printInorder(node) {> > if> (node ===> null> ) {> > return> ;> > }> > > // First recur on left subtree> > printInorder(node.left);> > > // Now deal with the node> > console.log(node.data);> > > // Then recur on right subtree> > printInorder(node.right);> }> // Driver code> const root => new> Node(1);> root.left => new> Node(2);> root.right => new> Node(3);> root.left.left => new> Node(4);> root.left.right => new> Node(5);> root.right.right => new> Node(6);> // Function call> console.log(> 'Inorder traversal of binary tree is: '> );> printInorder(root);>

Produktion

Inorder traversal of binary tree is: 4 2 5 1 3 6

Forklaring:

Hvordan inorder traversal virker

Kompleksitetsanalyse:

Tidskompleksitet: O(N) hvor N er det samlede antal knudepunkter. Fordi den krydser alle noderne mindst én gang.
Hjælpeplads: O(1), hvis der ikke tages hensyn til et rekursionsstabelrum. Ellers O(h), hvor h er højden af træet

I værste fald, h kan være det samme som N (når træet er et skævt træ)
I bedste tilfælde, h kan være det samme som berolige (når træet er et komplet træ)

Brugstilfælde af Inorder Traversal:

I tilfælde af BST (Binary Search Tree), hvis der på noget tidspunkt er behov for at få noderne i ikke-faldende rækkefølge, er den bedste måde at implementere en inorder-gennemgang.

Relaterede artikler: