EUKLIDISKE ALGORITMER (BASIC OG EXTENDED) - TECHCODEVIEW.COM

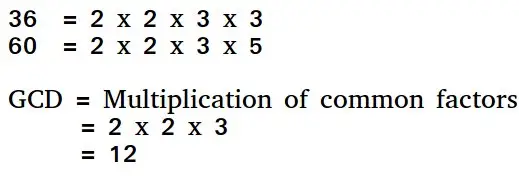
Den euklidiske algoritme er en måde at finde den største fælles divisor af to positive heltal. GCD af to tal er det største tal, der deler dem begge. En simpel måde at finde GCD på er at faktorisere begge tal og gange fælles primfaktorer.

GCD

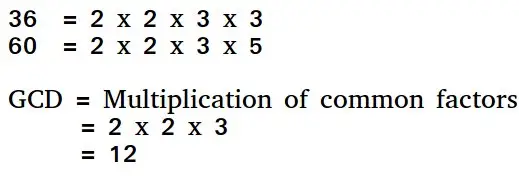
Grundlæggende euklidisk algoritme for GCD:

Algoritmen er baseret på nedenstående fakta.

Hvis vi trækker et mindre tal fra et større (vi reducerer et større tal), ændres GCD ikke. Så hvis vi bliver ved med at trække den største af to gentagne gange, ender vi med GCD.
I stedet for subtraktion, hvis vi dividerer det mindre tal, stopper algoritmen, når vi finder resten 0.

Nedenfor er en rekursiv funktion til at evaluere gcd ved hjælp af Euclids algoritme:

C

// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 35, b = 10;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 31, b = 2;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > return> 0;> }>

CPP

// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 35, b = 10;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 31, b = 2;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > return> 0;> }>

Java

// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a ==> 0> )> > return> b;> > return> gcd(b % a, a);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > int> a => 10> , b => 15> , g;> > > // Function call> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 35> ;> > b => 10> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 31> ;> > b => 2> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // Code Contributed by Mohit Gupta_OMG>

Python3

# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> > if> a> => => 0> :> > return> b> > return> gcd(b> %> a, a)> # Driver code> if> __name__> => => '__main__'> :> > a> => 10> > b> => 15> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 35> > b> => 10> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 31> > b> => 2> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> # Code Contributed By Mohit Gupta_OMG>

C#

// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> > }> > // Driver Code> > static> public> void> Main()> > {> > int> a = 10, b = 15, g;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 35;> > b = 10;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 31;> > b = 2;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // This code is contributed by ajit>

PHP

// php program to demonstrate Basic Euclidean Algorithm>

 // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) {  if ($a == 0)  return $b;  return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ',   gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ',   gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ',   gcd($a, $b); // This code is contributed by m_kit ?>>

Javascript

// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> > let a = 10, b = 15;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 35, b = 10;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 31, b = 2;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> // This code contributed by aashish1995>

Produktion

GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1

Tidskompleksitet: O(Log min(a, b))
Hjælpeplads: O(Log (min(a,b))

Udvidet euklidisk algoritme:

Udvidet euklidisk algoritme finder også heltalskoefficienter x og y således, at: ax + by = gcd(a, b)

Eksempler:

Input: a = 30, b = 20
Produktion: gcd = 10, x = 1, y = -1
(Bemærk, at 30*1 + 20*(-1) = 10)

Input: a = 35, b = 15
Produktion: gcd = 5, x = 1, y = -2
(Bemærk, at 35*1 + 15*(-2) = 5)

Den udvidede euklidiske algoritme opdaterer resultaterne af gcd(a, b) ved hjælp af resultaterne beregnet af det rekursive kald gcd(b%a, a). Lad værdierne af x og y beregnet af det rekursive kald være x ₁og y ₁. x og y opdateres ved hjælp af nedenstående udtryk.

axe + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x ₁+ er ₁
ax + by = (b%a)x ₁+ er ₁
ax + by = (b – [b/a] * a)x ₁+ er ₁
ax + by = a(y ₁– [b/a] * x ₁) + bx ₁

Sammenligning af LHS og RHS,
x = y ₁– ?b/a? * x ₁
y = x ₁

Anbefalet praksis Udvidet euklidisk algoritme Prøv det!

Nedenfor er en implementering af ovenstående tilgang:

C++

// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of> > // recursive call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Code> int> main()> {> > int> x, y, a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > cout < <> 'GCD('> < < a < <> ', '> < < b> > < <> ') = '> < < g < < endl;> > return> 0;> }>

C

// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of recursive> > // call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Program> int> main()> {> > int> x, y;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > printf> (> 'gcd(%d, %d) = %d'> , a, b, g);> > return> 0;> }>

Java

// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> int> x,> > int> y)> > {> > // Base Case> > if> (a ==> 0> ) {> > x => 0> ;> > y => 1> ;> > return> b;> > }> > int> x1 => 1> ,> > y1 => 1> ;> // To store results of recursive call> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using results of recursive> > // call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > // Driver Program> > public> static> void> main(String[] args)> > {> > int> x => 1> , y => 1> ;> > int> a => 35> , b => 15> ;> > int> g = gcdExtended(a, b, x, y);> > System.out.print(> 'gcd('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }>

Python3

# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> > # Base Case> > if> a> => => 0> :> > return> b,> 0> ,> 1> > gcd, x1, y1> => gcdExtended(b> %> a, a)> > # Update x and y using results of recursive> > # call> > x> => y1> -> (b> /> /> a)> *> x1> > y> => x1> > return> gcd, x, y> # Driver code> a, b> => 35> ,> 15> g, x, y> => gcdExtended(a, b)> print> (> 'gcd('> , a,> ','> , b,> ') = '> , g)>

C#

// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> > int> x,> int> y)> > {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results of> > // recursive call> > int> x1 = 1, y1 = 1;> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using> > // results of recursive call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > > // Driver Code> > static> public> void> Main ()> > {> > int> x = 1, y = 1;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, x, y);> > Console.WriteLine(> 'gcd('> + a +> ' , '> +> > b +> ') = '> + g);> > }> }>

PHP

 // PHP program to demonstrate  // working of extended  // Euclidean Algorithm // PHP function for  // extended Euclidean  // Algorithm function gcdExtended($a, $b,   $x, $y) {  // Base Case  if ($a == 0)  {  $x = 0;  $y = 1;  return $b;  }  // To store results   // of recursive call  $gcd = gcdExtended($b % $a,   $a, $x, $y);  // Update x and y using  // results of recursive  // call  $x = $y - floor($b / $a) * $x;  $y = $x;  return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>>

Javascript

> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> > x, y)> {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results> > // of recursive call> > let gcd = gcdExtended(b % a,> > a, x, y);> > // Update x and y using> > // results of recursive> > // call> > x = y - (b / a) * x;> > y = x;> > return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(> 'gcd('> + a);> document.write(> ', '> + b +> ')'> );> document.write(> ' = '> + g);> >

Output:

gcd(35, 15) = 5

Tidskompleksitet: O(log N)
Hjælpeplads: O(log N)

Hvordan fungerer udvidet algoritme?

Som det ses ovenfor, er x og y resultater for input a og b,

a.x + b.y = gcd —-(1)

Og x ₁og y ₁er resultater for input b%a og a

(b%a).x ₁+ a.y ₁= gcd

Når vi sætter b%a = (b – (?b/a?).a) ovenfor,
vi følger med. Bemærk, at ?b/a? er etage(b/a)

(b – (?b/a?).a).x ₁+ a.y ₁= gcd

Ovenstående ligning kan også skrives som nedenfor

b.x ₁+ a.(og ₁– (?b/a?).x ₁) = gcd —(2)

Efter at have sammenlignet koefficienter for 'a' og 'b' i (1) og
(2), vi følger,
x = y ₁– ?b/a? * x ₁
y = x ₁

Hvordan er udvidet algoritme nyttig?

Den udvidede euklidiske algoritme er især nyttig, når a og b er coprime (eller gcd er 1). Da x er den modulære multiplikative inverse af en modulo b, og y er den modulære multiplikative inverse af b modulo a. Især er beregningen af den modulære multiplikative inverse et væsentligt trin i RSA public-key krypteringsmetoden.