Et binært træ er afbalanceret, hvis højden af ​​træet er O(Log n), hvor n er antallet af noder. For eksempel bevarer AVL-træet O(Log n)-højden ved at sikre, at forskellen mellem højden af ​​venstre og højre undertræ er højst 1. Rød-sorte træer bevarer O(Log n)-højden ved at sikre, at tallet af sorte noder på hver rod-til-blad-sti er den samme, og at der ikke er nogen tilstødende røde noder. Balancerede binære søgetræer er præstationsmæssigt gode, da de giver O(log n) tid til søgning, indsættelse og sletning.

Et balanceret binært træ er et binært træ, der følger de 3 betingelser:

• Højden på venstre og højre træ for enhver node afviger ikke med mere end 1.
• Det venstre undertræ af den node er også afbalanceret.
• Det højre undertræ af den node er også afbalanceret.

En enkelt node er altid afbalanceret. Det omtales også som et højdebalanceret binært træ.

Eksempel :

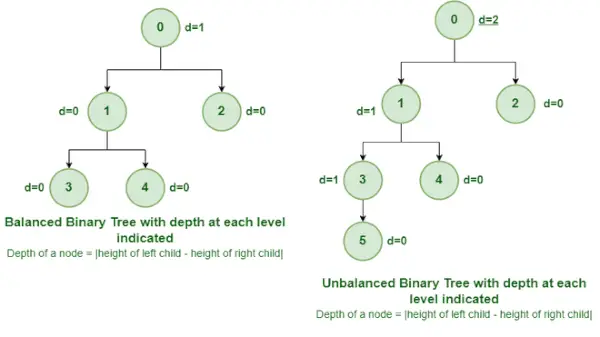
Balanceret og ubalanceret binært træ

Det er en type binært træ, hvor forskellen mellem højden af ​​venstre og højre undertræ for hver knude er enten 0 eller 1. I figuren ovenfor er rodknuden med værdien 0 ubalanceret med en dybde på 2 enheder .

Anvendelse af balanceret binært træ:

• AVL træer
• Rødt sort træ
• Balanceret binært søgetræ

Fordele ved Balanced Binary Tree:

• Ikke-destruktive opdateringer understøttes af et balanceret binært træ med samme asymptotiske effektivitet.
• Områdeforespørgsler og iteration i den rigtige rækkefølge gøres mulige af det afbalancerede binære træ.