Formel for vinkel mellem to vektorer

Vinklen mellem to vektorer er vinklen mellem deres haler, og denne vinkel kan let findes ved hjælp af krydsprodukt og prikprodukt af vektorformler. Vinklen mellem to vektorer ligger altid mellem 0° og 180°.
I denne artikel vil vi lære om, vinkel mellem to vektorer, definition, formler og eksempler i detaljer.
Hvad er vinkel mellem to vektorer?
Vinklen mellem to vektorer er den vinkel, der dannes ved skæringspunktet mellem deres haler. Vinklen mellem to vektorer kan være spids, højre eller stump, afhængigt af retningen af vektorerne.
Vinklen mellem to vektorer findes ved hjælp af to formler:
- Brug af punktprodukt af vektorer
- Brug af krydsprodukt af vektorer
Dette er forklaret i formlen nedenfor.
Vinkel mellem to vektorformler
Vinkel mellem to vektorer er let og oftest fundet ved brug af skalarprodukt af vektorer.

To vektor A og B
Prik produkt af A og B er givet af,
vec{A}.vec{B} = |A| |B| cosθ.
Særlige tilfælde
- Når vinklen mellem vektorer er 0 grader.
Det vil sige θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Når vinklen mellem vektorer er 180 grader.
⇒ |A| |B| cosθ
⇒ |A| |B| 180°
⇒ – |A| |B| [cos180° = -1]
- Når vinklen mellem vektorer er 90 grader.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Formel for vinkel mellem to vektorer
Cosinus af vinklen mellem to vektorer er lig med summen af produktet af de individuelle bestanddele af de to vektorer divideret med produktet af størrelsen af de to vektorer.
To vektorer A og B
cosθ=
θ= cos -1
I kartesisk form,
A = A x i + A og j + A Med k
B= B x i + B og j + B Med k
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Dot-produktets egenskaber
- Punktprodukt er kommutativt
vec{A}.vec{B}=vec{B}.vec{A}
- Dot-produktet er distribuerende
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Vinklen mellem to vektorer ligger mellem 0 ≤ θ ≤ 180. Når begge vektorers hale eller hoved falder sammen, så beregnes vinklen mellem vektorer.
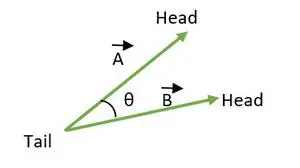
Halen falder sammen
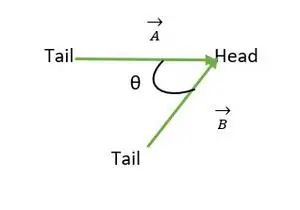
Hovedet er sammenfaldende
Eksempel på problemer Vinkel mellem to vektorer formel
Opgave 1: Find vinklen mellem vektorer (hvis de danner en ligesidet trekant)
- a og b vektorer
- b og c vektorer
- a og c vektorer
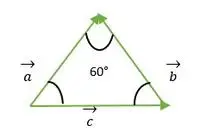
Ligesidet trekant dannet af a, b, c vektor
Løsning:
- a og b vektorer
For vektor a og b falder hovedet af begge vektorer sammen med hinanden, hvorfor vinklen mellem a og b vektor er den samme som vinklen mellem to sider af ligesidet trekant = 60°.
- b og c vektorer:
Fra ovenstående figur ser vi, at b- og c-vektorens hoved eller hale ikke falder sammen.
Så ved at bruge egenskaben forbliver en vektor uændret, hvis den transmitteres parallelt med sig selv.
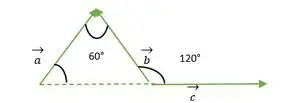
Vektor c forskydes parallelt med sig selv
Nu ser vi halen af vektorerne b og c er sammenfaldende med hinanden, derfor er den samme som den ydre vinkel gør med en ligesidet trekant = 120°.
- a og c vektorer

Halen på a og c falder sammen
For vektorerne a og c falder halen af begge vektorer sammen med hinanden, hvorfor vinklen mellem a- og c-vektoren er den samme som vinklen mellem to sider af den ligesidede trekant = 60°.
Opgave 2: Find vinkler mellem vektorer, hvis de danner en ligebenet retvinklet trekant.
- a og b vektor
- b og c vektor
- a og c vektorer
Løsning:
- a og b vektor

Ret vinkel Ligebenet trekant
Fra ovenstående figur ser vi, at hoved eller hale af a og b vektor ikke falder sammen. Så ved at bruge egenskaben forbliver en vektor uændret, hvis den transmitteres parallelt med sig selv.
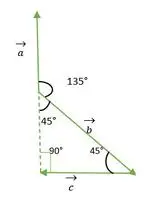
en vektor forskydes parallelt med sig selv
Nu falder a og b vektorhalerne sammen med hinanden og danner en vinkel, der er den samme som den udvendige vinkel på en retvinklet ligebenet trekant = 135°.
- b og c vektor

Ret vinkel Ligebenet trekant
Fra ovenstående figur falder b og c vektorhoved eller haler ikke sammen med hinanden. Så ved at bruge egenskaben forbliver en vektor uændret, hvis den transmitteres parallelt med sig selv.
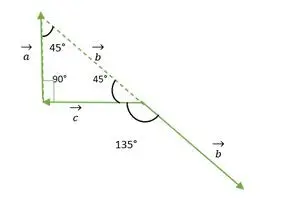
b vektor forskydes parallelt med sig selv
Nu falder b- og c-vektorernes haler sammen med hinanden og danner en vinkel, der er den samme som den udvendige vinkel på en retvinklet ligebenet trekant = 135°.
- a og c vektorer

Ret vinkel Ligebenet trekant
Fra ovenstående figur falder a og c vektorhoved eller haler ikke sammen med hinanden. Så ved at bruge egenskaben forbliver en vektor uændret, hvis den transmitteres parallelt med sig selv.
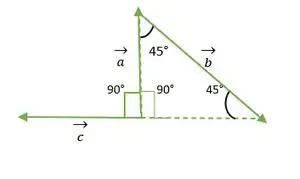
c vektor flyttes parallelt med sig selv
Nu falder a- og c-vektorernes haler sammen med hinanden og danner en vinkel, der er den samme som den retvinklede vinkel på en ligebenet trekant = 90°.
Opgave 3: Find vinkel mellem vektorerne A = i + j + k og vektor B = -2i – 2j – 2k.
Løsning:
Fra formlen,
A = A x i + A og j + A Med k
B= B x i + B og j + B Med k
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her i det givne spørgsmål,
A= i + j + k
B= -2i -2j -2k
Erstatning af værdierne i formlen
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Opgave 4: Find vinklen mellem vektor A = 3i + 4j og B = 2i + j
Løsning:
A = A x i + A og j + A Med k
B = B x i + B og j + B Med k
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her givet,
A= 3i + 4j + 0k
B= 2i + j + 0k
Ved at erstatte værdierne i formlen,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos -1 (
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos -1 (
frac{2}{(sqrt{5})} )
Opgave 5: Find vinklen mellem vektor A = i + j og vektor B = j + k.
Løsning:
Fra formlen,
A = A x i + A og j + A Med k
B = B x i + B og j + B Med k
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her i det givne spørgsmål,
⇒ A = i + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos -1 (1/2)
⇒ θ = 60°