Unit Circle: Definice, Vzorec, Diagram a Řešené příklady
Jednotková kružnice je kružnice, jejíž poloměr je 1. Střed jednotkové kružnice je v počátku (0,0) na ose. The obvod Unit Circle je 2π jednotek, zatímco plocha Unit Circle je π jednotek 2 . Nese všechny vlastnosti Circle. Unit Circle má rovnici x 2 + a 2 = 1. Tento jednotkový kruh pomáhá při definování různých trigonometrických pojmů.

Jednotkový kruh
Unit Circle je často označován jako S 1 zobecnění do vyšších dimenzí je jednotková sféra. Podívejme se podrobněji na příklady Unit Circle, Vzorec a Solved níže.
Co je Unit Circle?
Unit Circle je kruh, který má poloměr jednotky One(1). Pomocí kartézské roviny nakreslíme jednotkovou kružnici a jednotková kružnice je 2-stupňový polynom se dvěma proměnnými. Jednotkový kruh má různé aplikace v trigonometrii a algebře a používá se hlavně k nalezení hodnot různých trigonometrických poměrů, jako je sin x, cos x, tan x a další.
Definice kruhu jednotky
V matematice definujeme jednotkovou kružnici jako místo pevného bodu, který je ve vzdálenosti jedné jednotky od středu kružnice. Jednotková kružnice má poloměr jedné jednotky a odtud název jednotková kružnice.
Rovnice jednotkového kruhu
Víme, že rovnice libovolné kružnice se středem (h, k) a poloměrem „r“ je,
(x – h) 2 + (y – k) 2 = r 2
Pro jednotkovou kružnici víme, že r je 1 jednotka, takže rovnice jednotkové kružnice je,
(x – h) 2 + (y – k) 2 = 1
Vzorec jednotkového kruhu
Pokud je střed jednotkové kružnice počátek, tj. (h, k) = (0, 0), pak rovnice jednotkové kružnice je,
X 2 + a 2 = 1
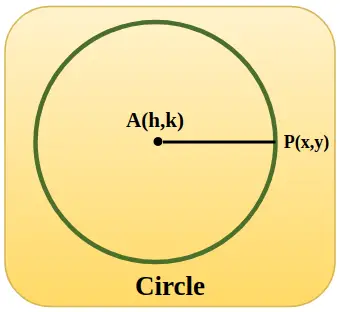
Jednotková kružnice je znázorněna na obrázku přidaném níže, se středovými souřadnicemi h, k, a když je kružnice na počátku, hodnota ha k je nula a poloměr AP je roven 1 jednotce.
Goniometrické funkce pomocí Unit Circle
K pochopení goniometrických funkcí lze lépe využít aplikaci Pythagorovy věty v jednotkovém kruhu. Za tímto účelem považujeme pravoúhlý trojúhelník za umístěný uvnitř jednotkové kružnice v kartézské rovině souřadnic. Pokud si všimneme, poloměr této kružnice označuje přeponu pravoúhlého trojúhelníku.
Poloměr kružnice tvoří vektor. To vede k vytvoření úhlu, řekněme θ, s kladnou osou x. Předpokládejme, že x je základní délka a y je výška nadmořské výšky pravoúhlého trojúhelníku. Souřadnice koncových bodů vektoru poloměru jsou také (x, y).
Pravoúhlý trojúhelník obsahuje strany 1, x a y. Trigonometrický poměr lze nyní vypočítat takto:
sin θ = Nadmořská výška/Hypotenuse = y/1
cos θ = základ/hypotenza = x/1
Nyní,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Dosazením hodnot θ můžeme získat hlavní hodnoty všech goniometrických funkcí. Obdobně jsou nalezeny hodnoty goniometrických funkcí v různých hodnotách.
Unit Circle s Sin Cos a Tan
Jakýkoli bod na jednotkové kružnici se souřadnicemi (x, y) je reprezentován pomocí goniometrických identit jako, (cosθ, sinθ). Souřadnice rohů poloměru představují kosinus a sinus hodnot θ pro konkrétní hodnotu θ a přímku poloměru. Máme cos θ = x a sin θ = y. V jednom kvadrantu jsou čtyři části kruhu, z nichž každá svírá úhel 90°, 180°, 270° a 360°. Hodnoty poloměru leží mezi -1 až 1. Také hodnoty sin θ a cos θ leží mezi 1 a -1 v tomto pořadí.
Jednotkový kruh a goniometrické identity
Trigonometrické identity jednotkového kruhu pro kotangens, sekans a kosekans lze vypočítat pomocí identit pro sin, cos a tan. Nakonec získáme pravoúhlý trojúhelník se stranami 1, x a y. Výpočet identit jednotkového kruhu lze vyjádřit jako,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sec 6 = 1/x
- cosec θ = 1/y
- dětská postýlka θ = x/y
Jednotkový kruhový graf
Jednotkový kruhový graf je graf, který obsahuje hodnotu trigonometrické funkce sinus a kosinus pro různé úhly. Jednotkový kruhový graf pro totéž je přidán níže,
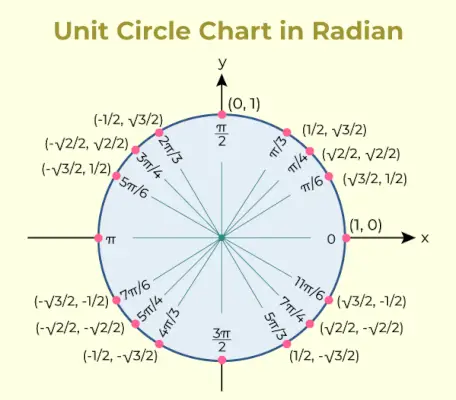
Unit Circle Table
Trigonometrické poměry použité v tabulce jednotkové kružnice se používají k výpisu souřadnic bodů na jednotkové kružnici, které odpovídají společným úhlům.
| Úhly | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| bez | 0 | 1/2 | 1/√ (2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√ (2) | 1/2 | 0 |
| tak | 0 | 1/√ (3) | 1 | √ (3) | Není definovaný |
| csc | Není definovaný | 2 | √ (2) | 23) | 1 |
| sek | 1 | 23) | √ (2) | 2 | Není definovaný |
| dětská postýlka | Není definovaný | √ (3) | 1 | 1/√ (3) | 0 |
Jednotkový kruh Pythagorejské identity
Existují tři pythagorejské identity a všechny lze snadno dokázat pomocí konceptu jednotkového kruhu, což jsou tři pythagorejské identity,
- bez 2 θ + cos 2 θ = 1
- 1 + tak 2 θ = sek 2 i
- 1 + dětská postýlka 2 θ = kosec 2 i
Jednotka Kruhová Komplexní Rovina
Komplexní čísla a Komplexní rovina lze snadno vysvětlit pomocí konceptu jednotkové kružnice. Rovnice jednotkového kruhu v komplexním tvaru je,
|z| = 1
NEBO
X 2 + a 2 = 1
V Eulerově formě je komplexní číslo reprezentováno jako,
z = e to = náklady t + i (sin t)
Přečtěte si více
Řešené příklady na Unit Circle
Q1: Dokažte, že bod Q leží na jednotkové kružnici, Q = [1/√(6), √4/√6]
Řešení:
vzhledem k tomu,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Rovnice jednotkového kruhu je,
X 2 + a 2 = 1
LHS = (1/√(6)) 2 + (√4/√6) 2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Bod Q[1/√(6), √4/√6] tedy neleží na jednotkové kružnici.
Q2: Vypočítejte tak 30 Ó pomocí hodnot sin a cos jednotkového kruhu.
Řešení:
opálení 30° s použitím hodnot sin a cos,
opálení 30° = (sin 30°)/ (cos 30°)
- bez 30° = 1/2
- cos 30° = √(3)/2
opálení 30° = 1/2/√(3)/2
opálení 30° = 1/√(3)
Q3: Ověřte, zda bod P [1/2, √(3)/2] leží na jednotkové kružnici.
Řešení:
vzhledem k tomu,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Rovnice jednotkového kruhu je,
- X 2 + a 2 = 1
LHS
= (1/2) 2 + (√(3)/2) 2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Procvičte si otázky na Unit Circle
Q1. Zkontrolujte, zda body A (1/2, 3/2) leží na jednotkové kružnici.
Q2. Zkontrolujte, zda body A (2, 1/2) leží na jednotkové kružnici.
Q3. Najděte hodnotu cos 240°
Q4. Najděte hodnotu tan 320°
Q5. Najděte hodnotu hříchu 160°
Unit Circle – FAQ
Co je Unit Circle?
Jednotková kružnice je definována jako umístění bodu jednu jednotku od pevného bodu. Má střed v (0,0) a hodnota jeho poloměru je 1.
Jak zkontrolovat, zda bod leží na jednotkovém kruhu?
Libovolný bod ležící ve 2D rovině, který má tvar (x, y), se vloží do jednotkové kružnice x 2 + a 2 = 1 pro ověření, zda leží na kružnici nebo ne.
Jaký je vzorec Unit Circle?
Vzorec jednotkového kruhu je vzorec, který se používá k algebraickému znázornění jednotkového kruhu. Vzorec jednotkového kruhu je dán jako,
X 2 + a 2 = 1
Proč se tomu říká Unit Circle?
Jednotková kružnice se nazývá jednotková kružnice, protože má poloměr jedné (1) jednotek.