Vytiskněte všechny způsoby, jak rozbít řetězec ve formě držáku
Vzhledem k řetězci najděte všechny způsoby, jak rozbít daný řetězec ve formě držáku. Přiložte každé podřetězec v závorce.
Příklady:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Důrazně doporučujeme, abyste minimalizovali váš prohlížeč a nejprve to zkuste sami.
Záměrem je použít rekurzi. Udržujeme dva parametry - index dalšího znaku, který má být zpracován, a dosud výstupní řetězec. Začínáme od indexu dalšího znaku, který bude zpracován, připojený podřennost vytvořená nezpracovaným řetězcem do výstupního řetězce a opakujeme se na zbývajícím řetězci, dokud nezpracováme celý řetězec. K vytvoření výstupního řetězce používáme std :: subst. SubSt (POS n) Vrací podřetězec délky n, který začíná v poloze POS aktuálního řetězce.
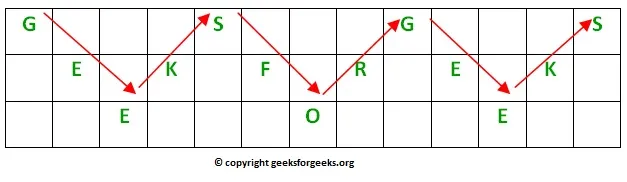
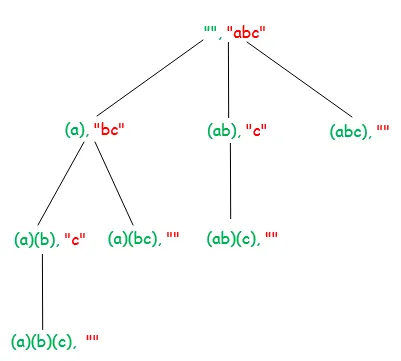
Níže uvedený diagram zobrazuje strom rekurze pro vstupní řetězec „ABC“. Každý uzel na diagramu ukazuje zpracovaný řetězec (označený zelenou) a nezpracovaný řetězec (označený červenou).

Níže je uvedena implementace výše uvedené myšlenky
C++ // C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include using namespace std ; // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far void findCombinations ( string str int index string out ) { if ( index == str . length ()) cout < < out < < endl ; for ( int i = index ; i < str . length (); i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substr ( index i + 1 - index ) + ')' ); } } // Driver Code int main () { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); return 0 ; }
Java // Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations ( String str int index String out ) { if ( index == str . length ()) System . out . println ( out ); for ( int i = index ; i < str . length (); i ++ ) // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substring ( index i + 1 ) + ')' ); } // Driver Code public static void main ( String [] args ) { // input string String str = 'abcd' ; findCombinations ( str 0 '' ); } } // Contributed by Pramod Kumar
Python3 # Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations ( string index out ): if index == len ( string ): print ( out ) for i in range ( index len ( string ) 1 ): # append substring formed by str[index # i] to output string findCombinations ( string i + 1 out + '(' + string [ index : i + 1 ] + ')' ) # Driver Code if __name__ == '__main__' : # input string string = 'abcd' findCombinations ( string 0 '' ) # This code is contributed by # sanjeev2552
C# // C# program to find all combinations // of Non-overlapping substrings formed // from given string using System ; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations ( string str int index string @out ) { if ( index == str . Length ) { Console . WriteLine ( @out ); } for ( int i = index ; i < str . Length ; i ++ ) { // append substring formed by // str[index i] to output string findCombinations ( str i + 1 @out + '(' + str . Substring ( index ( i + 1 ) - index ) + ')' ); } } // Driver Code public static void Main ( string [] args ) { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); } } // This code is contributed by Shrikant13
JavaScript // Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations ( string index out ) { if ( index == string . length ) { console . log ( out ); } for ( let i = index ; i < string . length ; i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( string i + 1 out + '(' + string . substring ( index i + 1 ) + ')' ); } } // Driver Code const string = 'abcd' ; findCombinations ( string 0 '' ); // contributed by adityasharmadev01
Výstup
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Složitost času: O (n 2 )
Pomocný prostor: O (n 2 )