Předpoklad: Úvod do ukazatelů

Zvažte následující program:

C

#include> int> main()> {> > int> arr[5] = { 1, 2, 3, 4, 5 };> > int> *ptr = arr;> > printf> (> '%p '> , ptr);> > return> 0;> }>

Ve výše uvedeném programu máme ukazatel ptr což ukazuje na 0 ^čt prvek pole. Podobně můžeme také deklarovat ukazatel, který může ukazovat na celé pole namísto pouze jednoho prvku pole. Tento ukazatel je užitečný, když mluvíme o vícerozměrných polích.

Syntax:

data_type  (* var_name ) [size_of_array]; 

Tady:

datový_typ je typ dat, která pole obsahuje. var_name je název proměnné ukazatele. size_of_array je velikost pole, na které bude ukazatel ukazovat.

Příklad

int (*ptr)[10]; 

Tady ptr je ukazatel, který může ukazovat na pole 10 celých čísel. Vzhledem k tomu, že dolní index má vyšší prioritu než nepřímost, je nutné uvést operátor nepřímosti a název ukazatele do závorek. Zde je typem ptr ‚ukazatel na pole 10 celých čísel.

Poznámka: Ukazatel, který ukazuje na 0 ^čt prvek pole a ukazatel, který ukazuje na celé pole, jsou zcela odlišné. Ukazuje to následující program:

C

// C program to understand difference between> // pointer to an integer and pointer to an> // array of integers.> #include> int> main()> {> > // Pointer to an integer> > int> *p;> > > // Pointer to an array of 5 integers> > int> (*ptr)[5];> > int> arr[5];> > > // Points to 0th element of the arr.> > p = arr;> > > // Points to the whole array arr.> > ptr = &arr;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > > p++;> > ptr++;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > > return> 0;> }>

Výstup

p = 0x7fff6463e890, ptr = 0x7fff6463e890 p = 0x7fff6463e894, ptr = 0x7fff6463e8a4 

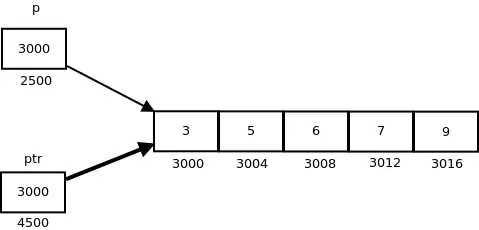
Tady, p je ukazatel na 0 ^čt prvek pole arr , zatímco ptr je ukazatel, který ukazuje na celé pole arr .

• Základní typ p je int, zatímco základní typ ptr je „pole 5 celých čísel“.
• Víme, že aritmetika ukazatele se provádí vzhledem k základní velikosti, takže pokud napíšeme ptr++, pak ukazatel ptr se posune dopředu o 20 bajtů.

Následující obrázek ukazuje ukazatel p a ptr. Tmavší šipka označuje ukazatel na pole.

Při dereferencování ukazatelového výrazu získáme hodnotu, na kterou ukazuje tento ukazatelový výraz. Ukazatel na pole ukazuje na pole, takže při jeho dereferencování bychom měli dostat pole a název pole označuje základní adresu. Kdykoli je tedy ukazatel na pole dereferencován, získáme základní adresu pole, na které ukazuje.

C

// C program to illustrate sizes of> // pointer of array> #include> int> main()> {> > int> arr[] = { 3, 5, 6, 7, 9 };> > int> *p = arr;> > int> (*ptr)[5] = &arr;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > printf> (> '*p = %d, *ptr = %p '> , *p, *ptr);> > > printf> (> 'sizeof(p) = %lu, sizeof(*p) = %lu '> ,> > sizeof> (p),> sizeof> (*p));> > printf> (> 'sizeof(ptr) = %lu, sizeof(*ptr) = %lu '> ,> > sizeof> (ptr),> sizeof> (*ptr));> > return> 0;> }>

Výstup

p = 0x7fff55adbff0, ptr = 0x7fff55adbff0 *p = 3, *ptr = 0x7fff55adbff0 sizeof(p) = 8, sizeof(*p) = 4 sizeof(ptr) = 8, sizeof(*ptr) = 20 

Ukazatel na vícerozměrná pole

1. Ukazatele a dvourozměrná pole

Ve dvourozměrném poli můžeme přistupovat ke každému prvku pomocí dvou indexů, kde první index představuje číslo řádku a druhý index představuje číslo sloupce. K prvkům 2-D pole lze přistupovat také pomocí notace ukazatele. Předpokládejme, že arr je 2-D pole, můžeme přistupovat k libovolnému prvku arr[i][j] pole pomocí ukazatelového výrazu *(*(arr + i) + j) . Nyní uvidíme, jak lze tento výraz odvodit.
Vezměme si dvourozměrné pole arr[3][4] :

int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };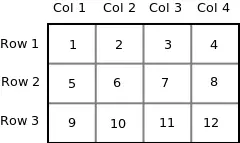 

Protože paměť v počítači je organizována lineárně, není možné ukládat 2-D pole do řádků a sloupců. Koncept řádků a sloupců je pouze teoretický, ve skutečnosti je 2-D pole uloženo v hlavním pořadí, tj. řádky jsou umístěny vedle sebe. Následující obrázek ukazuje, jak bude výše uvedené 2D pole uloženo do paměti.

Každý řádek lze považovat za 1-D pole, takže dvourozměrné pole lze považovat za kolekci jednorozměrných polí, která jsou umístěna jedno po druhém. Jinými slovy, můžeme říci, že 2-D dimenzionální pole, která jsou umístěna jedno po druhém. Tak tady arr je pole 3 prvků, kde každý prvek je 1-D pole 4 celých čísel.
Víme, že název pole je konstantní ukazatel, který ukazuje na 0 ^čt 1-D pole a obsahuje adresu 5000. Od arr je ‚ukazatel na pole 4 celých čísel‘, podle aritmetiky ukazatele bude výraz arr + 1 představovat adresu 5016 a výraz arr + 2 bude představovat adresu 5032.
Takže to můžeme říct arr ukazuje na 0 ^čt 1-D pole, arr + 1 ukazuje na 1 ^Svatý 1-D pole a arr + 2 ukazuje na 2 ^nd 1-D pole.

Obecně můžeme napsat:

 arr + i Points to ith element of arr ->Ukazuje na to 1-D pole 

• Protože arr + i ukazuje na i ^čt prvek arr , při dereferencování dostane i ^čt prvek arr což je samozřejmě 1-D pole. Tedy výraz *(arr + i) nám dává základní adresu i ^čt 1-D pole.
• Víme, ukazatelový výraz *(arr + i) je ekvivalentní s výrazem dolní index arr[i] . Tak *(arr + i) což je stejné jako arr[i] nám dává základní adresu i ^čt 1-D pole.
• Pro přístup k jednotlivému prvku našeho 2-D pole bychom měli mít přístup k jakémukoli j ^čt prvek i ^čt 1-D pole.
• Vzhledem k tomu, základní typ *(arr + i) je int a obsahuje adresu 0 ^čt prvek i ^čt 1-D pole, můžeme získat adresy následujících prvků v i ^čt 1-D pole přidáním celočíselných hodnot do *(arr + i) .
• Například *(arr + i) + 1 bude představovat adresu 1 ^Svatý prvek 1 ^Svatý prvek i ^čt 1-D pole a *(arr+i)+2 bude představovat adresu 2 ^nd prvek i ^čt 1-D pole.
• Podobně *(arr + i) + j bude představovat adresu j ^čt prvek i ^čt 1-D pole. Dereferencováním tohoto výrazu můžeme dostat j ^čt prvek i ^čt 1-D pole.

Ukazatele a trojrozměrná pole

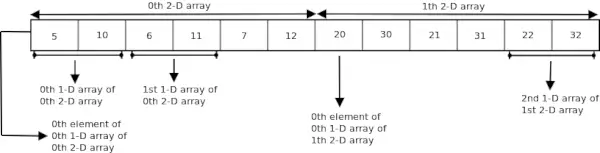
int arr[2][3][2] = { {{5, 10}, {6, 11}, {7, 12}}, {{20, 30}, {21, 31}, {22, 32}} }; 

V trojrozměrném poli můžeme přistupovat ke každému prvku pomocí tří indexů. Vezměme si 3-D pole- Trojrozměrné pole můžeme považovat za pole 2-D pole, tj. každý prvek 3-D pole je považován za 2-D pole. 3-D pole arr lze považovat za pole sestávající ze dvou prvků, kde každý prvek je 2-D pole. Název pole arr je ukazatel na 0 ^čt 2-D pole.

Tedy ukazatelový výraz *(*(*(arr + i ) + j ) + k) je ekvivalentní k výrazu dolního indexu arr[i][j][k].
Víme, že výraz *(arr + i) je ekvivalentní arr[i] a výraz *(*(arr + i) + j) je ekvivalentní arr[i][j]. Můžeme tedy říci, že arr[i] představuje základní adresu i ^čt 2-D pole a arr[i][j] představuje základní adresu j ^čt 1-D pole.

Příklad

Níže uvedený příklad ukazuje program pro tisk prvků 3D pole pomocí ukazatelů.

C

// C program to print the elements of 3-D> // array using pointer notation> #include> int> main()> {> > int> arr[2][3][2] = {> > {> > {5, 10},> > {6, 11},> > {7, 12},> > },> > {> > {20, 30},> > {21, 31},> > {22, 32},> > }> > };> > int> i, j, k;> > for> (i = 0; i <2; i++)> > {> > for> (j = 0; j <3; j++)> > {> > for> (k = 0; k <2; k++)> > printf> (> '%d '> , *(*(*(arr + i) + j) +k));> > printf> (> ' '> );> > }> > }> > return> 0;> }>

Výstup

5 10 6 11 7 12 20 30 21 31 22 32 

Následující obrázek ukazuje, jak je 3-D pole použité ve výše uvedeném programu uloženo v paměti.

Subscripting ukazatele na pole

Předpokládat arr je 2-D pole se 3 řádky a 4 sloupci a ptr je ukazatel na pole 4 celých čísel a ptr obsahuje základní adresu pole arr .

int arr[3][4] = {{10, 11, 12, 13}, {20, 21, 22, 23}, {30, 31, 32, 33}}; int (*ptr)[4]; ptr = arr;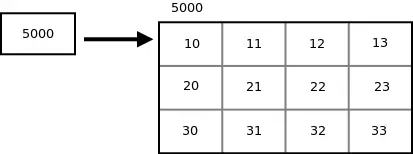 

Od té doby ptr je ukazatel na první řádek 2-D pole, tj. pole 4 celých čísel, ptr + i bude ukazovat na i ^čt řádek. Na dereferencování ptr + i , získáme základní adresu i ^čt řádek. Pro přístup na adresu j ^čt prvek i ^čt řádek můžeme přidat j do ukazatelového výrazu *(ptr + i) . Tedy ukazatelový výraz *(ptr + i) + j uvádí adresu j ^čt prvek i ^čt řádek a výraz ukazatele *(*(ptr + i)+j) udává hodnotu j ^čt prvek i ^čt řádek.
Víme, že ukazatelový výraz *(*(ptr + i) + j) je ekvivalentní výrazu dolního indexu ptr[i][j]. Takže pokud máme proměnnou ukazatele obsahující základní adresu 2-D pole, pak můžeme přistupovat k prvkům pole dvojitým indexováním této proměnné ukazatele.

Příklad

C

// C program to print elements of a 2-D array> // by scripting a pointer to an array> #include> int> main()> {> > int> arr[3][4] = {> > {10, 11, 12, 13},> > {20, 21, 22, 23},> > {30, 31, 32, 33}> > };> > int> (*ptr)[4];> > ptr = arr;> > printf> (> '%p %p %p '> , ptr, ptr + 1, ptr + 2);> > printf> (> '%p %p %p '> , *ptr, *(ptr + 1), *(ptr + 2));> > printf> (> '%d %d %d '> , **ptr, *(*(ptr + 1) + 2), *(*(ptr + 2) + 3));> > printf> (> '%d %d %d '> , ptr[0][0], ptr[1][2], ptr[2][3]);> > return> 0;> }>

Výstup

0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 10 22 33 10 22 33