DISKRÉTNÍ MATEMATICKÉ SVAZY - DISKRÉTNÍ MATEMATIKA

Nechť L je neprázdná množina uzavřená dvěma binárními operacemi zvanými meet and join, označovanými ∧ a ∨. Pak se L nazývá mřížka, pokud platí následující axiomy, kde a, b, c jsou prvky v L:

1) Komutativní zákon: -
(a) a ∧ b = b ∧ a (b) a ∨ b = b ∨ a

2) Asociační zákon:-
(a) (a ∧ b)∧ c = a ∧(b∧ c) (b) (a ∨ b) ∨ c = a ∨ (b ∨ c)

3) Absorpční zákon: -
(a) a ∧ ( a ∨ b) = a (b) a ∨ ( a ∧ b) = a

Dualita:

Duál libovolného výroku v mřížce (L,∧ ,∨ ) je definován jako výrok získaný záměnou ∧ an ∨.

Například , duál a ∧ (b ∨ a) = a ∨ a je a ∨ (b ∧ a )= a ∧ a

Ohraničené mřížky:

Mřížka L se nazývá ohraničená, pokud má největší prvek 1 a nejmenší prvek 0.

Příklad:

Množina P(S) množiny S při operacích průniku a sjednocení je omezená mřížka, protože ∅ je nejmenší prvek P(S) a množina S je největší prvek P(S).
Množina +ve celého čísla I ₊pod obvyklým řádem ≦ není ohraničená mřížka, protože má nejmenší prvek 1, ale největší prvek neexistuje.

Vlastnosti ohraničených mřížek:

Je-li L omezená mřížka, pak pro jakýkoli prvek a ∈ L máme následující identity:

a ∨ 1 = 1
a ∧1= a
a ∨0=a
a ∧0=0

Teorém: Dokažte, že každá konečná mřížka L = {a ₁,A ₂,A ₃....A _n} je ohraničený.

Důkaz: Dali jsme konečnou mřížku:

L = {a ₁,A ₂,A ₃....A _n}

Největším prvkem mřížek L je tedy a ₁∨ a ₂∨ a _{3∨.....∨a _n.}

Také nejmenší prvek mřížky L je a ₁∧ a ₂∧a ₃∧....∧a _n.

Protože pro každou konečnou mřížku existují největší a nejmenší prvky. L je tedy ohraničené.

Dílčí mřížky:

Uvažujme neprázdnou podmnožinu L ₁mřížky L. Poté L ₁se nazývá podmřížka L, pokud L ₁samo o sobě je mřížka, tj. operace L, tj. a ∨ b ∈ L ₁a a ∧ b ∈ L ₁kdykoli ∈ L ₁a b ∈ L ₁.

Příklad: Uvažujme mřížku všech +ve celých čísel I ₊za operace dělitelnosti. Mříž D _nze všech dělitelů n > 1 je podmřížka I ₊.

Určete všechny dílčí mřížky D ₃₀které obsahují alespoň čtyři prvky, D ₃₀={1,2,3,5,6,10,15,30}.

Řešení: Dílčí mřížky D ₃₀které obsahují alespoň čtyři prvky, jsou následující:

1. {1, 2, 6, 30} 2. {1, 2, 3, 30}
3. {1, 5, 15, 30} 4. {1, 3, 6, 30}
5. {1, 5, 10, 30} 6. {1, 3, 15, 30}
7. {2, 6, 10, 30}

Izomorfní mřížky:

Dvě mříže L ₁a L ₂se nazývají izomorfní mřížky, pokud existuje bijekce z L ₁k L ₂tj. f: L ₁⟶ L ₂, takže f (a ∧ b) =f(a)∧ f(b) a f (a ∨ b) = f (a) ∨ f (b)

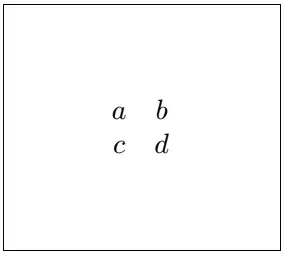
Příklad: Určete, zda jsou mřížky zobrazené na obr izomorfní.

Řešení: Mřížky zobrazené na obr jsou izomorfní. Uvažujme zobrazení f = {(a, 1), (b, 2), (c, 3), (d, 4)}. Například f (b ∧ c) = f (a) = 1. mají f (b) ∧ f(c) = 2 ∧ 3 = 1

Distribuční mřížka:

Mřížka L se nazývá distributivní mřížka, pokud pro libovolné prvky a, b a c z L splňuje následující distribuční vlastnosti:

a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)

Pokud mřížka L nesplňuje výše uvedené vlastnosti, nazývá se nedistributivní mřížka.

Příklad:

Výkonová množina P (S) množiny S při operaci průniku a sjednocení je distribuční funkcí. Od té doby,
a ∩ (b ∪ c) = (a ∩ b) ∪ (a ∩ c)
a také a ∪ (b ∩ c) = (a ∪ b) ∩ (a ∪c) pro libovolné množiny a, b a c P(S).
Mříž zobrazená na obr. II je distributivní. Vzhledem k tomu, že splňuje distribuční vlastnosti pro všechny objednané trojice, které jsou převzaty z 1, 2, 3 a 4.

Doplňky a doplněné mřížky:

Nechť L je omezená mřížka s dolní hranicí o a horní hranicí I. Nechť a je prvkem, jestliže L. Prvek x v L nazýváme doplňkem a, jestliže a ∨ x = I a a ∧ x = 0

O mřížce L se říká, že je doplněná, pokud je L omezená a každý prvek v L má doplněk.

Příklad: Určete doplněk a a c na obr.

Řešení: Doplněk a je d. Protože a ∨ d = 1 a a ∧ d = 0

Doplněk c neexistuje. Protože neexistuje žádný prvek c takový, že c ∨ c'=1 a c ∧ c'= 0.

Modulární mříž:

Mřížka (L, ∧,∨) se nazývá modulární mřížka, jestliže a ∨ (b ∧ c) = (a ∨ b) ∧ c vždy, když a ≦ c.

Přímý součin mřížek:

Nechte (L ₁∨ ₁∧ ₁) a (L ₂∨ ₂∧ ₂) být dvě mřížky. Pak (L, ∧,∨) je přímý součin mříží, kde L = L ₁x L ₂ve které jsou binární operace ∨(join) a ∧(meet) na L takové, že pro libovolný (a ₁,b ₁) a (a ₂,b ₂) v L.