Ford-Fulkersonův algoritmus je široce používaný algoritmus pro řešení problému maximálního toku v tokové síti. Problém maximálního toku zahrnuje určení maximálního množství toku, které lze poslat ze zdrojového vrcholu do klesajícího vrcholu v orientovaném váženém grafu, s výhradou kapacitních omezení na okrajích.

Algoritmus funguje tak, že iterativně najde rozšiřující cestu, což je cesta od zdroje k jímce v grafu zbytků, tj. grafu získaném odečtením toku proudu od kapacity každé hrany. Algoritmus pak zvýší tok podél této cesty o maximální možnou hodnotu, což je minimální kapacita hran podél cesty.

Problém:

Je dán graf, který představuje síť toků, kde každá hrana má kapacitu. Také vzhledem ke dvěma vrcholům zdroj „s“ a dřez „t“ v grafu najděte maximální možný průtok od s do t s následujícími omezeními:

• Tok na hraně nepřekračuje danou kapacitu hrany.
• Příchozí tok se rovná odchozímu toku pro každý vrchol kromě sat.

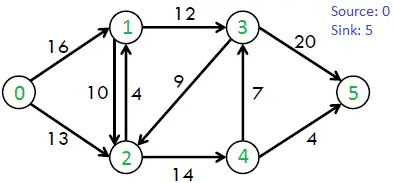
Vezměme si například následující graf z knihy CLRS.

Maximální možný průtok ve výše uvedeném grafu je 23.

Doporučený postup Najděte maximální průtok Vyzkoušejte!

Předpoklad : Úvod do problému maximálního průtoku

Ford-Fulkersonův algoritmus

Následuje jednoduchá myšlenka Ford-Fulkersonova algoritmu:

1. Začněte s počátečním tokem jako 0.
2. Zatímco existuje rozšiřující cesta od zdroje k jímce:
   • Najděte rozšiřující cestu pomocí libovolného algoritmu hledání cesty, jako je prohledávání do šířky nebo prohledávání do hloubky.
   • Určete množství toku, které lze poslat podél rozšiřující cesty, což je minimální zbytková kapacita podél okrajů cesty.
   • Zvyšte průtok podél augmentační dráhy o určené množství.
3. Vraťte maximální průtok.

Časová náročnost: Časová složitost výše uvedeného algoritmu je O(max_flow * E). Spustíme smyčku, zatímco existuje rozšiřující cesta. V nejhorším případě můžeme přidat 1 jednotkový tok v každé iteraci. Proto se časová složitost stává O(max_flow * E).

Jak implementovat výše uvedený jednoduchý algoritmus?
Nejprve definujme koncept reziduálního grafu, který je potřebný pro pochopení implementace.

Zbytkový graf průtokové sítě je graf, který ukazuje další možný průtok. Pokud v grafu zbytků existuje cesta od zdroje k propadu, pak je možné přidat průtok. Každá hrana zbytkového grafu má hodnotu tzv zbytková kapacita což se rovná původní kapacitě hrany mínus průtok proudu. Zbytková kapacita je v podstatě aktuální kapacita hrany.

Promluvme si nyní o detailech implementace. Zbytková kapacita je 0, pokud mezi dvěma vrcholy reziduálního grafu není žádná hrana. Můžeme inicializovat zbytkový graf jako původní graf, protože neexistuje žádný počáteční tok a zpočátku se zbytková kapacita rovná původní kapacitě. Abychom našli rozšiřující cestu, můžeme buď provést BFS nebo DFS zbytkového grafu. V níže uvedené implementaci jsme použili BFS. Pomocí BFS můžeme zjistit, zda existuje cesta od zdroje k jímce. BFS také vytváří parent[] pole. Pomocí pole parent[] procházíme nalezenou cestu a najdeme možný průtok touto cestou nalezením minimální zbytkové kapacity podél cesty. Později přidáme tok nalezené cesty k celkovému toku.

Důležité je, že musíme aktualizovat zbytkové kapacity v grafu zbytků. Odečteme tok cesty od všech hran podél cesty a přidáme tok cesty podél reverzních hran Potřebujeme přidat tok cesty podél reverzních hran, protože později může být nutné poslat tok v opačném směru (viz například následující odkaz).

Níže je uvedena implementace Ford-Fulkersonova algoritmu. Aby to bylo jednoduché, graf je reprezentován jako 2D matice.

C++

// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> > 't' in residual graph. Also fills parent[] to store the> > path */> bool> bfs(> int> rGraph[V][V],> int> s,> int> t,> int> parent[])> {> > // Create a visited array and mark all vertices as not> > // visited> > bool> visited[V];> > memset> (visited, 0,> sizeof> (visited));> > // Create a queue, enqueue source vertex and mark source> > // vertex as visited> > queue <> int> >q;> > q.push(s);> > visited[s] => true> ;> > parent[s] = -1;> > // Standard BFS Loop> > while> (!q.empty()) {> > int> u = q.front();> > q.pop();> > for> (> int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Pokud najdeme spojení se sink nodem, // pak už v BFS nemá smysl Musíme // jen nastavit jeho rodiče a můžeme vrátit // true if (v == t) { parent[ v] = u; vrátit true; } q.push(v); rodič[v] = u; navštíveno[v] = true; } } } // Nedosáhli jsme sink v BFS počínaje zdrojem, takže // return false return false; } // Vrátí maximální průtok od s do t v daném grafu int fordFulkerson(int graf[V][V], int s, int t) { int u, v; // Vytvořte reziduální graf a vyplňte reziduální graf // danými kapacitami v původním grafu jako // reziduálními kapacitami v reziduálním grafu int rGraph[V] [V]; // Reziduální graf kde rGraph[i][j] // udává zbytkovou kapacitu hrany // od i do j (pokud tam hrana je. Pokud // rGraph[i][j] je 0, tak není) for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; int parent[V]; // Toto pole je vyplněno BFS a // ukládá cestu int max_flow = 0 // Na začátku není žádný tok // Rozšiřte tok, když existuje cesta od zdroje k // propadu while (bfs(rGraph, s, t, parent)) { // Najděte minimální zbytkovou kapacitu hran podél // cesty vyplněné BFS Nebo můžeme říci najít // maximální tok nalezenou cestou int cesta_tok = INT_MAX pro (v = t; v != s; v = rodič[v]) { u = parent[v]; cesta_tok = min(cesta_tok, rGraph[u][v] } // aktualizace zbytkových kapacit hran a // obrácení hran podél cesty pro (v = t; v != s; v =); rodič[v]) { u = rodič[v]; rGraph[u][v] -= cesta_tok; // Vrátí celkový tok return max_flow; } // Program ovladače pro testování výše uvedených funkcí int main() { // Vytvořme graf zobrazený ve výše uvedeném příkladu int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout < < 'The maximum possible flow is ' < < fordFulkerson(graph, 0, 5); return 0; }>

Jáva

// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> > static> final> int> V => 6> ;> // Number of vertices in graph> > /* Returns true if there is a path from source 's' to> > sink 't' in residual graph. Also fills parent[] to> > store the path */> > boolean> bfs(> int> rGraph[][],> int> s,> int> t,> int> parent[])> > {> > // Create a visited array and mark all vertices as> > // not visited> > boolean> visited[] => new> boolean> [V];> > for> (> int> i => 0> ; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Pokud najdeme spojení se sink // uzlem, pak už v BFS // není žádný smysl Musíme pouze nastavit jeho rodič // a může vrátit true if (v == t) { parent[ v] = u; vrátit true; } queue.add(v); rodič[v] = u; navštíveno[v] = true; } } } // Nedosáhli jsme sink v BFS počínaje zdrojem, // takže return false return false; } // Vrátí maximální průtok od s do t v daném // grafu int fordFulkerson(int graf[][], int s, int t) { int u, v; // Vytvořte zbytkový graf a vyplňte zbytkový // graf danými kapacitami v původním grafu // jako zbytkové kapacity v grafu zbytků // Zbytkový graf kde rGraph[i][j] označuje // zbytkovou kapacitu hrany od i do j (pokud // je hrana. Je-li rGraph[i][j] 0, pak // není) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; // Toto pole je vyplněno BFS a pro uložení cesty int parent[] = new int[ V] int max_flow = 0 // Na začátku není žádný tok // Rozšiřte tok, když existuje cesta od zdroje // k propadu while (bfs(rGraph, s, t, parent)) { // Najděte minimální zbytkovou kapacitu; hran // podél cesty vyplněné BFS Nebo můžeme říci // najít maximální průtok nalezenou cestou int cesta_tok = Integer.MAX_VALUE for (v = t; v != s; v = parent[v ]) { u = parent[v]; cesta_tok = Math.min(cesta_tok, rGraph[u][v] } // aktualizace zbytkových kapacit hran a // obrácení hran podél cesty pro (v = t; v != s; v = rodič[v]) { u = rodič[v]; rGraph[u][v] -= tok_cesty[v][u] += tok_cesty } // Přidat tok cesty k celkovému; flow max_flow += path_flow } // Vrátí celkový tok return max_flow } // Ovladač pro testování výše uvedených funkcí public static void main(String[] args) throws java.lang.Exception { // Vytvořme zobrazený graf; ve výše uvedeném příkladu int graf[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); System.out.println('Maximální možný průtok je ' + m.fordFulkerson(graph, 0, 5)); } }>

Krajta

# Python program for implementation> # of Ford Fulkerson algorithm> from> collections> import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> > def> __init__(> self> , graph):> > self> .graph> => graph> # residual graph> > self> . ROW> => len> (graph)> > # self.COL = len(gr[0])> > '''Returns true if there is a path from source 's' to sink 't' in> > residual graph. Also fills parent[] to store the path '''> > def> BFS(> self> , s, t, parent):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> self> .ROW)> > # Create a queue for BFS> > queue> => []> > # Mark the source node as visited and enqueue it> > queue.append(s)> > visited[s]> => True> > # Standard BFS Loop> > while> queue:> > # Dequeue a vertex from queue and print it> > u> => queue.pop(> 0> )> > # Get all adjacent vertices of the dequeued vertex u> > # If a adjacent has not been visited, then mark it> > # visited and enqueue it> > for> ind, val> in> enumerate> (> self> .graph[u]):> > if> visited[ind]> => => False> and> val>> 0> :> > # If we find a connection to the sink node,> > # then there is no point in BFS anymore> > # We just have to set its parent and can return true> > queue.append(ind)> > visited[ind]> => True> > parent[ind]> => u> > if> ind> => => t:> > return> True> > # We didn't reach sink in BFS starting> > # from source, so return false> > return> False> > > > # Returns the maximum flow from s to t in the given graph> > def> FordFulkerson(> self> , source, sink):> > # This array is filled by BFS and to store path> > parent> => [> -> 1> ]> *> (> self> .ROW)> > max_flow> => 0> # There is no flow initially> > # Augment the flow while there is path from source to sink> > while> self> .BFS(source, sink, parent) :> > # Find minimum residual capacity of the edges along the> > # path filled by BFS. Or we can say find the maximum flow> > # through the path found.> > path_flow> => float> (> 'Inf'> )> > s> => sink> > while> (s !> => source):> > path_flow> => min> (path_flow,> self> .graph[parent[s]][s])> > s> => parent[s]> > # Add path flow to overall flow> > max_flow> +> => path_flow> > # update residual capacities of the edges and reverse edges> > # along the path> > v> => sink> > while> (v !> => source):> > u> => parent[v]> > self> .graph[u][v]> -> => path_flow> > self> .graph[v][u]> +> => path_flow> > v> => parent[v]> > return> max_flow> > # Create a graph given in the above diagram> graph> => [[> 0> ,> 16> ,> 13> ,> 0> ,> 0> ,> 0> ],> > [> 0> ,> 0> ,> 10> ,> 12> ,> 0> ,> 0> ],> > [> 0> ,> 4> ,> 0> ,> 0> ,> 14> ,> 0> ],> > [> 0> ,> 0> ,> 9> ,> 0> ,> 0> ,> 20> ],> > [> 0> ,> 0> ,> 0> ,> 7> ,> 0> ,> 4> ],> > [> 0> ,> 0> ,> 0> ,> 0> ,> 0> ,> 0> ]]> g> => Graph(graph)> source> => 0> ; sink> => 5> > print> (> 'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav>

C#

// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> > static> readonly> int> V = 6;> // Number of vertices in> > // graph> > /* Returns true if there is a path> > from source 's' to sink 't' in residual> > graph. Also fills parent[] to store the> > path */> > bool> bfs(> int> [, ] rGraph,> int> s,> int> t,> int> [] parent)> > {> > // Create a visited array and mark> > // all vertices as not visited> > bool> [] visited => new> bool> [V];> > for> (> int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List fronta = nový seznam (); fronta.Přidat(y); navštíveno [s] = true; rodič[s] = -1; // Standardní smyčka BFS while (queue.Count != 0) { int u = queue[0]; queue.RemoveAt(0); for (int v = 0; v if (navštívené[v] == false && rGraph[u, v]> 0) { // Pokud najdeme spojení se sink // uzlem, pak v BFS nemá smysl / / už jen musíme nastavit jeho rodič // a může vrátit true if (v == t) { parent[v] = u } queue.Add(v] = u; v] = true; (int[, ] graf, int s, int t) { int u, v // Vytvořte zbytkový graf a vyplňte // graf zbytků danými // kapacitami v původním grafu jako // zbytkovými kapacitami v grafu zbytků //; / Reziduální graf kde rGraph[i,j] // udává zbytkovou kapacitu // hrany od i do j (pokud existuje // hrana. Pokud je rGraph[i,j] 0, pak // není) int [, ] rGraph = new int[V, V] for (u = 0; u for (v = 0; v rGraph[u, v] = graf[u, v]; // Toto pole je vyplněno BFS a k uložení cesty int[] parent = new int[V]; int max_flow = 0; // Na začátku není žádný tok // Rozšiřte tok, když existuje cesta od zdroje // k propadu while (bfs(rGraph, s, t, parent)) { // Najděte minimální zbytkovou kapacitu hran // podél cesty vyplněno BFS. Nebo můžeme říci // najít maximální průtok nalezenou cestou. int cesta_tok = int.MaxValue; for (v = t; v != s; v = rodič[v]) { u = rodič[v]; cesta_tok = Math.Min(cesta_tok, rGraf[u, v]); } // aktualizace zbytkové kapacity hran a // obrácení hran podél cesty for (v = t; v != s; v = rodič[v]) { u = rodič[v]; rGraph[u, v] -= tok_cesty; rGraph[v, u] += tok_cesty; } // Přidání toku cesty k celkovému toku max_flow += tok_cesty; } // Vrátí celkový tok return max_flow; } // Kód ovladače public static void Main() { // Vytvořme graf zobrazený ve výše uvedeném příkladu int[, ] graph = new int[, ] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); Console.WriteLine('Maximální možný tok je ' + m.fordFulkerson(graf, 0, 5)); } } /* Tento kód přispěl PrinceRaj1992 */>

Javascript

> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > > // Create a visited array and mark all> > // vertices as not visited> > let visited => new> Array(V);> > for> (let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Pokud najdeme spojení se sink // uzlem, pak už v BFS // není žádný smysl Musíme pouze nastavit jeho rodič // a může vrátit true if (v == t) { parent[ v] = u; vrátit true; } fronta.push(v); rodič[v] = u; navštíveno[v] = true; } } } // Nedosáhli jsme sink v BFS počínaje // ze zdroje, takže return false return false; } // Vrátí maximální průtok od s do t v // dané grafové funkci fordFulkerson(graph, s, t) { let u, v; // Vytvořte zbytkový graf a vyplňte // zbytkový graf danými kapacitami // v původním grafu jako zbytkové // kapacity ve zbytkovém grafu // Zbytkový graf kde rGraph[i][j] // označuje zbytkovou kapacitu hrany / / od i do j (pokud existuje hrana. // Pokud je rGraph[i][j] 0, pak je // není) nechť rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Toto pole je vyplněno BFS a pro uložení cesty let parent = new Array(V) // Na začátku není žádný tok let max_flow = 0 // Rozšiřte tok, když // existuje cesta od zdroje k jímce while (bfs(rGraph, s, t); , parent)) { // Najděte minimální zbytkovou kapacitu hran // podél cesty vyplněné BFS Nebo můžeme říci // najít maximální tok nalezenou cestou nech cesta_tok = Číslo.MAX_VALUE; ; v != s; v = rodič[v]) { u = rodič[v]; obrácené hrany podél cesty for(v = t; v != s; v = rodič[v]) { u = rodič[v]] -= tok_cesty[v][u] + = path_flow } // Přidání toku cesty k celkovému toku max_flow += path_flow } // Návrat celkového toku max_flow } // Kód ovladače // Vytvořme graf zobrazený ve výše uvedeném příkladu let graph = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('Maximální možný tok je ' + fordFulkerson(graf, 0, 5)); // Tento kód přispěl avanitrachhadiya2155>

Výstup

The maximum possible flow is 23 

Časová složitost: O(|V| * E^2) ,kde E je počet hran a V je počet vrcholů.

Prostorová složitost :O(V), jak jsme vytvořili frontu.

Výše uvedená implementace Ford Fulkerson Algorithm se nazývá Edmonds-Karpův algoritmus . Myšlenka Edmonds-Karpa je použít BFS v implementaci Ford Fulkerson, protože BFS vždy vybírá cestu s minimálním počtem hran. Při použití BFS lze časovou složitost v nejhorším případě snížit na O(VE ² ). Výše uvedená implementace používá reprezentaci matice sousedství, ačkoli BFS bere O(V ² ) čas, časová složitost výše uvedené implementace je O(EV ³ ) (Odkaz kniha CLRS pro důkaz časové náročnosti)

Toto je důležitý problém, který se objevuje v mnoha praktických situacích. Příklady zahrnují maximalizaci přepravy s danými provozními limity, maximalizaci toku paketů v počítačových sítích.
Dincův algoritmus pro Max-Flow.

Cvičení:
Upravte výše uvedenou implementaci tak, aby běžela v O(VE ² ) čas.