Dynamické programování je metoda používaná v matematice a informatice k řešení složitých problémů jejich rozdělením na jednodušší dílčí problémy. Řešením každého dílčího problému pouze jednou a uložením výsledků se vyhnete nadbytečným výpočtům, což vede k efektivnějším řešením pro širokou škálu problémů. Tento článek poskytuje podrobný průzkum konceptů dynamického programování ilustrovaný příklady.

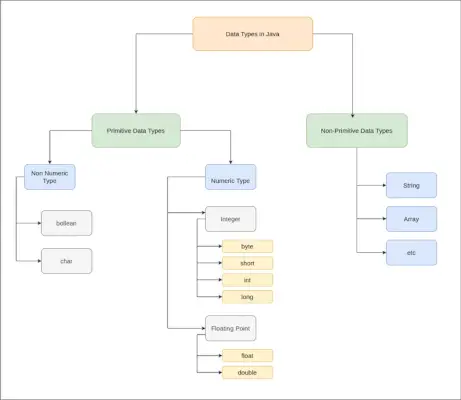
Dynamické programování

Obsah

• Co je dynamické programování?
• Jak funguje dynamické programování?
• Příklady dynamického programování
• Kdy použít dynamické programování?
• Přístupy dynamického programování
• Algoritmus dynamického programování
• Výhody dynamického programování
• Aplikace dynamického programování
• Naučte se základy dynamického programování
• Pokročilé koncepty dynamického programování
• Problémy dynamického programování

Co je dynamické programování (DP)?

Dynamické programování (DP) je metoda používaná v matematice a informatice k řešení složitých problémů jejich rozdělením na jednodušší dílčí problémy. Řešením každého dílčího problému pouze jednou a uložením výsledků se vyhnete nadbytečným výpočtům, což vede k efektivnějším řešením pro širokou škálu problémů.

Jak funguje dynamické programování (DP)?

• Identifikujte dílčí problémy: Rozdělte hlavní problém na menší, nezávislé dílčí problémy.
• Řešení prodejen: Vyřešte každý dílčí problém a uložte řešení do tabulky nebo pole.
• Build Up Solutions: Použijte uložená řešení k vytvoření řešení hlavního problému.
• Vyhněte se redundanci: Ukládáním řešení DP zajišťuje, že každý dílčí problém je vyřešen pouze jednou, čímž se zkracuje doba výpočtu.

Příklady dynamického programování (DP)

Příklad 1: Zvažte problém nalezení Fibonacciho posloupnosti:

Fibonacciho sekvence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Přístup hrubou silou:

Chcete-li najít n-té Fibonacciho číslo pomocí přístupu hrubé síly, jednoduše byste přidali (n-1). a (n-2). Fibonacciho čísla. To by fungovalo, ale pro velké hodnoty by to bylo neefektivní n , protože by to vyžadovalo výpočet všech předchozích Fibonacciho čísel.

Dynamický programovací přístup:

Fibonacciho řada využívající dynamické programování

• Dílčí problémy: F(0), F(1), F(2), F(3), …
• Řešení prodejen: Vytvořte tabulku pro uložení hodnot F(n) při jejich výpočtu.
• Build Up Solutions: Pro F(n) vyhledejte v tabulce F(n-1) a F(n-2) a sečtěte je.
• Vyhněte se redundanci: Tabulka zajišťuje, že každý dílčí problém (např. F(2)) je vyřešen pouze jednou.

Pomocí DP můžeme efektivně vypočítat Fibonacciho posloupnost, aniž bychom museli přepočítávat dílčí problémy.

Příklad 2: Nejdelší společná podsekvence (nalezení nejdelší podsekvence, která je společná pro dva řetězce)

Příklad 3: Nejkratší cesta v grafu (nalezení nejkratší cesty mezi dvěma uzly v grafu)

Příklad 4: Problém s batohem (zjištění maximální hodnoty položek, které lze umístit do batohu s danou kapacitou)

Kdy použít dynamické programování (DP)?

Dynamické programování je optimalizační technika používaná při řešení problémů, která se skládá z následujících charakteristik:

1. Optimální spodní struktura:

Optimální podstruktura znamená, že kombinujeme optimální výsledky dílčích problémů, abychom dosáhli optimálního výsledku většího problému.

Příklad:

Zvažte problém najít minimální náklady cesta ve váženém grafu z a zdroj uzel do a destinace uzel. Tento problém můžeme rozdělit na menší dílčí problémy:

• Najít minimální náklady cesta z zdroj uzel ke každému středně pokročilí uzel.
• Najít minimální náklady cesta od každého středně pokročilí uzel k destinace uzel.

Řešení většího problému (nalezení cesty s minimálními náklady ze zdrojového uzlu do cílového uzlu) lze sestavit z řešení těchto menších dílčích problémů.

2. Překrývající se dílčí problémy:

V různých částech problému se opakovaně řeší stejné dílčí problémy.

Příklad:

Zvažte problém výpočtu Fibonacciho řada . Chcete-li vypočítat Fibonacciho číslo v indexu n , potřebujeme spočítat Fibonacciho čísla u indexů n-1 a n-2 . To znamená, že podproblém výpočtu Fibonacciho čísla na indexu n-1 se používá dvakrát při řešení většího problému výpočtu Fibonacciho čísla v indexu n .

Přístupy dynamického programování (DP)

Dynamického programování lze dosáhnout dvěma způsoby:

1. Přístup shora dolů (zapamatování):

V přístupu shora dolů, známém také jako zapamatování , začneme s konečným řešením a rekurzivně jej rozložíme na menší podproblémy. Abychom se vyhnuli nadbytečným výpočtům, ukládáme výsledky vyřešených dílčích úloh do memoizační tabulky.

Pojďme si rozebrat přístup shora dolů:

• Začne s konečným řešením a rekurzivně jej rozdělí na menší dílčí problémy.
• Ukládá řešení dílčích problémů do tabulky, aby se zabránilo nadbytečným výpočtům.
• Vhodné, když je počet dílčích problémů velký a mnoho z nich je znovu použito.

2. Přístup zdola nahoru (tabulka):

V přístupu zdola nahoru, známém také jako tabelování , začínáme od nejmenších dílčích problémů a postupně se dostáváme ke konečnému řešení. Výsledky řešených dílčích úloh ukládáme do tabulky, abychom se vyhnuli nadbytečným výpočtům.

Pojďme si rozebrat přístup zdola nahoru:

• Začíná s nejmenšími dílčími problémy a postupně se staví ke konečnému řešení.
• Vyplní tabulku řešeními dílčích problémů způsobem zdola nahoru.
• Vhodné, když je počet dílčích problémů malý a optimální řešení lze přímo vypočítat z řešení menších dílčích problémů.

Dynamické programování (DP) Algoritmus

Dynamické programování je algoritmická technika, která řeší složité problémy jejich rozdělením na menší dílčí problémy a uložením jejich řešení pro budoucí použití. Je zvláště účinný při problémech, které obsahují překrývající se dílčí problémy a optimální spodní konstrukce.

Běžné algoritmy, které používají dynamické programování:

• Nejdelší společná podsekvence (LCS): Najde nejdelší společnou podsekvenci mezi dvěma řetězci.
• Nejkratší cesta v grafu: Vyhledá nejkratší cestu mezi dvěma uzly v grafu.
• Problém s batohem: Určuje maximální hodnotu položek, které lze umístit do batohu s danou kapacitou.
• Násobení maticového řetězce: Optimalizuje pořadí násobení matic, aby se minimalizoval počet operací.
• Fibonacciho sekvence: Vypočítá n-té Fibonacciho číslo.

Výhody dynamického programování (DP)

Dynamické programování má širokou škálu výhod, včetně:

• Zabraňuje opakovanému přepočítávání stejných dílčích problémů, což vede k výrazné úspoře času.
• Zajišťuje nalezení optimálního řešení zvážením všech možných kombinací.
• Rozděluje složité problémy na menší, lépe zvládnutelné dílčí problémy.

Aplikace dynamického programování (DP)

Dynamické programování má širokou škálu aplikací, včetně:

• Optimalizace: Problém batohu, problém nejkratší cesty, problém maximálního podpole
• Počítačová věda: Nejdelší společná podsekvence, editační vzdálenost, párování řetězců
• Operační výzkum: Řízení zásob, plánování, alokace zdrojů

Nyní se podívejme na komplexní plán pro zvládnutí dynamického programování.

Naučte se základy dynamického programování (DP)

• Co je zapamatování? Kompletní návod
• Tabulování vs Memoizace
• Optimální vlastnost spodní stavby
• Vlastnost překrývajících se dílčích problémů
• Jak vyřešit problém dynamického programování?

• Fibonacciho čísla
• n-té katalánské číslo
• Čísla zvonů (počet způsobů rozdělení sady)
• Binomický koeficient
• Problém s výměnou mincí
• Problém podmnožiny součtu
• Vypočítejte nCr % p
• Řezání tyče
• Algoritmus malování plotu
• Nejdelší společná posloupnost
• Nejdelší rostoucí subsekvence
• Nejdelší podsekvence taková, že rozdíl mezi sousedy je jedna
• Maximální velikost čtvercové podmatice se všemi 1
• Cesta minimálních nákladů
• Minimální počet skoků k dosažení konce
• Nejdelší společný podřetězec (řešení DP optimalizované pro prostor)
• Spočítejte způsoby, jak dosáhnout n-tého schodiště pomocí kroku 1, 2 nebo 3
• Spočítejte všechny možné cesty z matice mXn od levého horního do pravého dolního rohu
• Jedinečné cesty v mřížce s překážkami

2. Střední problémy dynamického programování (DP)

• Algoritmus Floyda Warshalla
• Bellman-Fordův algoritmus
• 0-1 Problém s batohem
• Potisk položek v 0/1 batohu
• Neohraničený batoh (opakování položek povoleno)
• Puzzle s vypouštěním vajíček
• Problém se zlomem slov
• Problém s krytím vertexu
• Problém se stohováním dlaždic
• Problém se stohováním krabic
• Problém s oddílem
• Problém obchodního cestujícího | Sada 1 (naivní a dynamické programování)
• Nejdelší palindromická podsekvence
• Nejdelší společná rostoucí subsekvence (LCS + LIS)
• Najděte všechny odlišné součty podmnožin (nebo podsekvencí) pole
• Vážené plánování práce
• Počítat odchylky (Permutace taková, že se žádný prvek neobjeví na své původní pozici)
• Minimální inzerce pro vytvoření palindromu
• Shoda vzoru zástupných znaků
• Způsoby uspořádání koulí tak, aby sousední koule byly různých typů

3. Těžké problémy dynamického programování (DP)

• Rozdělení palindromu
• Problém zalamování slov
• Malířův problém s oddílem
• Program pro problém s mostem a pochodní
• Násobení maticového řetězce
• Tisk závorek v Matrix Chain Multiplication Problem
• Obdélník maximálního součtu ve 2D matici
• Maximální zisk nákupem a prodejem podílu maximálně kkrát
• Minimální náklady na třídění řetězců pomocí operací obrácení různých nákladů
• Počet AP (aritmetický postup) subsekvencí v poli
• Úvod do dynamického programování na stromech
• Maximální výška stromu, kdy lze jakýkoli uzel považovat za kořen
• Nejdelší opakující se a nepřekrývající se podřetězec

Rychlé odkazy:

• Naučte se datovou strukturu a algoritmy | Výukový program DSA
• 20 nejčastějších otázek k pohovoru o dynamickém programování
• „Problémy procvičování“ dynamického programování
• „Kvíz“ o dynamickém programování