EL PROBLEMA DEL CÀTERER MANDRÓS

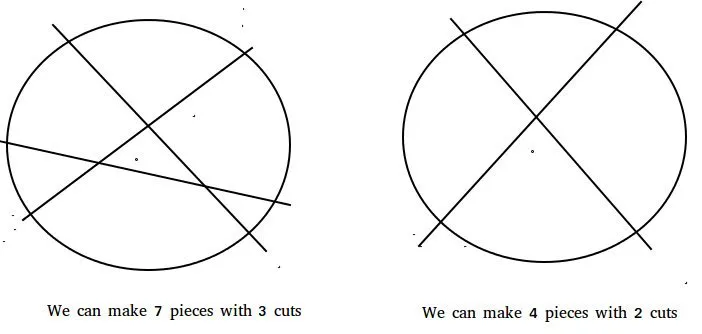
Tenint en compte un nombre enter que denota el nombre de talls que es poden fer en una crepe, trobeu el nombre màxim de peces que es poden formar fent n talls.
Exemples:

Input : n = 1 Output : 2 With 1 cut we can divide the pancake in 2 pieces Input : 2 Output : 4 With 2 cuts we can divide the pancake in 4 pieces Input : 3 Output : 7 We can divide the pancake in 7 parts with 3 cuts Input : 50 Output : 1276

Pràctica recomanada El problema del càterer mandrós Proveu -ho!

Let f(n) denote the maximum number of pieces that can be obtained by making n cuts. Trivially f(0) = 1 As there'd be only 1 piece without any cut. Similarly f(1) = 2 Proceeding in similar fashion we can deduce the recursive nature of the function. The function can be represented recursively as :   f(n) = n + f(n-1)   Hence a simple solution based on the above formula can run in O(n).

Podem optimitzar per sobre de la fórmula.

We now know  f(n) = n + f(n-1) Expanding f(n-1) and so on we have  f(n) = n + n-1 + n-2 + ...... + 1 + f(0) which gives f(n) = (n*(n+1))/2 + 1

Per tant, amb aquesta optimització podem respondre a totes les consultes a O (1).
A continuació, es mostra la implementació de la idea anterior:

C++

    // A C++ program to find the solution to   // The Lazy Caterer's Problem   #include          using     namespace     std  ;   // This function receives an integer n   // and returns the maximum number of   // pieces that can be made form pancake   // using n cuts   int     findPieces  (  int     n  )   {      // Use the formula      return     (  n     *     (     n     +     1  ))     /     2     +     1  ;   }   // Driver Code   int     main  ()   {      cout      < <     findPieces  (  1  )      < <     endl  ;      cout      < <     findPieces  (  2  )      < <     endl  ;      cout      < <     findPieces  (  3  )      < <     endl  ;      cout      < <     findPieces  (  50  )      < <     endl  ;      return     0  ;   }

Java

    // Java program to find the solution to   // The Lazy Caterer's Problem   import     java.io.*  ;   class   GFG      {      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      static     int     findPieces  (  int     n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }          // Driver program to test above function      public     static     void     main     (  String  []     args  )         {      System  .  out  .  println  (  findPieces  (  1  ));      System  .  out  .  println  (  findPieces  (  2  ));      System  .  out  .  println  (  findPieces  (  3  ));      System  .  out  .  println  (  findPieces  (  50  ));      }   }   // This code is contributed by Pramod Kumar

Python3

    # A Python 3 program to    # find the solution to   # The Lazy Caterer's Problem   # This function receives an    # integer n and returns the    # maximum number of pieces    # that can be made form    # pancake using n cuts   def   findPieces  (   n   ):   # Use the formula   return   (  n   *   (   n   +   1  ))   //   2   +   1   # Driver Code   print  (  findPieces  (  1  ))   print  (  findPieces  (  2  ))   print  (  findPieces  (  3  ))   print  (  findPieces  (  50  ))   # This code is contributed   # by ihritik

    // C# program to find the solution    // to The Lazy Caterer's Problem   using     System  ;   class     GFG      {      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      static     int     findPieces  (  int     n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }          // Driver code      public     static     void     Main     ()         {      Console  .  WriteLine  (  findPieces  (  1  ));      Console  .  WriteLine  (  findPieces  (  2  ));      Console  .  WriteLine  (  findPieces  (  3  ));      Console  .  Write  (  findPieces  (  50  ));      }   }   // This code is contributed by Nitin Mittal.

PHP

       // A php program to find    // the solution to The    // Lazy Caterer's Problem   // This function receives    // an integer n and returns    // the maximum number of   // pieces that can be made    // form pancake using n cuts   function   findPieces  (  $n  )   {   // Use the formula   return   (  $n   *   (   $n   +   1  ))   /   2   +   1  ;   }   // Driver Code   echo   findPieces  (  1  )      '  n  '   ;   echo   findPieces  (  2  )      '  n  '   ;   echo   findPieces  (  3  )      '  n  '   ;   echo   findPieces  (  50  )     '  n  '  ;   // This code is contributed   // by nitin mittal.    ?>

JavaScript

     <  script  >   // Javascript program to find the solution to   // The Lazy Caterer's Problem      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      function     findPieces  (  n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }       // Driver Code          document  .  write  (  findPieces  (  1  )     +     '  
'  );      document  .  write  (  findPieces  (  2  )     +     '  
'  );      document  .  write  (  findPieces  (  3  )     +     '  
'  );      document  .  write  (  findPieces  (  50  ));        <  /script>