Classificació ràpida
És un algorisme de tipus Divide & Conquer.
Dividir: Reorganitza els elements i divideix les matrius en dues submatrius i un element entre la cerca que cada element de la submatriu esquerra sigui menor o igual que l'element mitjà i cada element de la submatriu dreta sigui més gran que l'element central.
Conquerir: De manera recursiva, ordena dues submatrius.
Combina: Combina la matriu ja ordenada.
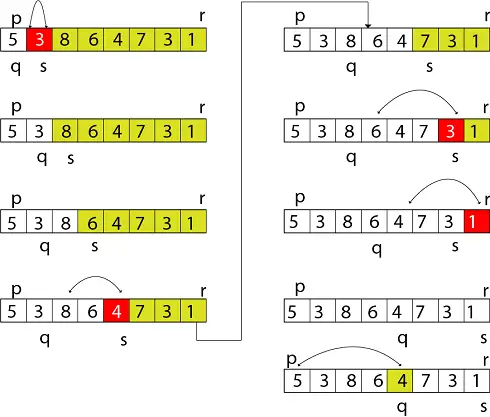
Algorisme:
QUICKSORT (array A, int m, int n) 1 if (n > m) 2 then 3 i ← a random index from [m,n] 4 swap A [i] with A[m] 5 o ← PARTITION (A, m, n) 6 QUICKSORT (A, m, o - 1) 7 QUICKSORT (A, o + 1, n)
Algoritme de partició:
L'algorisme de partició reordena les submatrius en un lloc.
PARTITION (array A, int m, int n) 1 x ← A[m] 2 o ← m 3 for p ← m + 1 to n 4 do if (A[p] <x) 1 5 6 7 8 then o ← + swap a[o] with a[p] a[m] return < pre> <p> <strong>Figure: shows the execution trace partition algorithm</strong> </p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort.webp" alt="DAA Quick sort"> <h3>Example of Quick Sort: </h3> <pre> 44 33 11 55 77 90 40 60 99 22 88 </pre> <p>Let <strong>44</strong> be the <strong>Pivot</strong> element and scanning done from right to left</p> <p>Comparing <strong>44</strong> to the right-side elements, and if right-side elements are <strong>smaller</strong> than <strong>44</strong> , then swap it. As <strong>22</strong> is smaller than <strong>44</strong> so swap them.</p> <pre> <strong>22</strong> 33 11 55 77 90 40 60 99 <strong>44</strong> 88 </pre> <p>Now comparing <strong>44</strong> to the left side element and the element must be <strong>greater</strong> than 44 then swap them. As <strong>55</strong> are greater than <strong>44</strong> so swap them.</p> <pre> 22 33 11 <strong>44</strong> 77 90 40 60 99 <strong>55</strong> 88 </pre> <p>Recursively, repeating steps 1 & steps 2 until we get two lists one left from pivot element <strong>44</strong> & one right from pivot element.</p> <pre> 22 33 11 <strong>40</strong> 77 90 <strong>44</strong> 60 99 55 88 </pre> <p> <strong>Swap with 77:</strong> </p> <pre> 22 33 11 40 <strong>44</strong> 90 <strong>77</strong> 60 99 55 88 </pre> <p>Now, the element on the right side and left side are greater than and smaller than <strong>44</strong> respectively.</p> <p> <strong>Now we get two sorted lists:</strong> </p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-2.webp" alt="DAA Quick sort"> <p>And these sublists are sorted under the same process as above done.</p> <p>These two sorted sublists side by side.</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-3.webp" alt="DAA Quick sort"> <br> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-4.webp" alt="DAA Quick sort"> <h3>Merging Sublists:</h3> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-5.webp" alt="DAA Quick sort"> <p> <strong> SORTED LISTS</strong> </p> <p> <strong>Worst Case Analysis:</strong> It is the case when items are already in sorted form and we try to sort them again. This will takes lots of time and space.</p> <h3>Equation:</h3> <pre> T (n) =T(1)+T(n-1)+n </pre> <p> <strong>T (1)</strong> is time taken by pivot element.</p> <p> <strong>T (n-1)</strong> is time taken by remaining element except for pivot element.</p> <p> <strong>N:</strong> the number of comparisons required to identify the exact position of itself (every element)</p> <p>If we compare first element pivot with other, then there will be 5 comparisons.</p> <p>It means there will be n comparisons if there are n items.</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-6.webp" alt="DAA Quick sort"> <h3>Relational Formula for Worst Case:</h3> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-7.webp" alt="DAA Quick sort"> <h3>Note: for making T (n-4) as T (1) we will put (n-1) in place of '4' and if <br> We put (n-1) in place of 4 then we have to put (n-2) in place of 3 and (n-3) <br> In place of 2 and so on. <p>T(n)=(n-1) T(1) + T(n-(n-1))+(n-(n-2))+(n-(n-3))+(n-(n-4))+n <br> T (n) = (n-1) T (1) + T (1) + 2 + 3 + 4+............n <br> T (n) = (n-1) T (1) +T (1) +2+3+4+...........+n+1-1</p> <p>[Adding 1 and subtracting 1 for making AP series]</p> <p>T (n) = (n-1) T (1) +T (1) +1+2+3+4+........ + n-1 <br> T (n) = (n-1) T (1) +T (1) + <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-8.webp" alt="DAA Quick sort">-1</p> <p> <strong>Stopping Condition: T (1) =0</strong> </p> <p>Because at last there is only one element left and no comparison is required.</p> <p>T (n) = (n-1) (0) +0+<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-8.webp" alt="DAA Quick sort">-1</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-9.webp" alt="DAA Quick sort"> <p> <strong>Worst Case Complexity of Quick Sort is T (n) =O (n<sup>2</sup>)</strong> </p> <h3>Randomized Quick Sort [Average Case]:</h3> <p>Generally, we assume the first element of the list as the pivot element. In an average Case, the number of chances to get a pivot element is equal to the number of items.</p> <pre> Let total time taken =T (n) For eg: In a given list p 1, p 2, p 3, p 4............pn If p 1 is the pivot list then we have 2 lists. I.e. T (0) and T (n-1) If p2 is the pivot list then we have 2 lists. I.e. T (1) and T (n-2) p 1, p 2, p 3, p 4............pn If p3 is the pivot list then we have 2 lists. I.e. T (2) and T (n-3) p 1, p 2, p 3, p 4............p n </pre> <p>So in general if we take the <strong>Kth</strong> element to be the pivot element.</p> <p> <strong>Then,</strong> </p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-10.webp" alt="DAA Quick sort"> <p>Pivot element will do n comparison and we are doing average case so,</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-11.webp" alt="DAA Quick sort"> <p> <strong>So Relational Formula for Randomized Quick Sort is:</strong> </p> <pre> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-12.webp" alt="DAA Quick sort"> = n+1 +<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-13.webp" alt="DAA Quick sort">(T(0)+T(1)+T(2)+...T(n-1)+T(n-2)+T(n-3)+...T(0)) <br> = n+1 +<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-13.webp" alt="DAA Quick sort">x2 (T(0)+T(1)+T(2)+...T(n-2)+T(n-1)) </pre> <pre> n T (n) = n (n+1) +2 (T(0)+T(1)+T(2)+...T(n-1)........eq 1 </pre> <p>Put n=n-1 in eq 1</p> <pre> (n -1) T (n-1) = (n-1) n+2 (T(0)+T(1)+T(2)+...T(n-2)......eq2 </pre> <p>From eq1 and eq 2</p> <p>n T (n) - (n-1) T (n-1)= n(n+1)-n(n-1)+2 (T(0)+T(1)+T(2)+?T(n-2)+T(n-1))-2(T(0)+T(1)+T(2)+...T(n-2)) <br> n T(n)- (n-1) T(n-1)= n[n+1-n+1]+2T(n-1) <br> n T(n)=[2+(n-1)]T(n-1)+2n <br> n T(n)= n+1 T(n-1)+2n</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-14.webp" alt="DAA Quick sort"> <p>Put n=n-1 in eq 3</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-15.webp" alt="DAA Quick sort"> <p>Put 4 eq in 3 eq</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-16.webp" alt="DAA Quick sort"> <p>Put n=n-2 in eq 3</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-17.webp" alt="DAA Quick sort"> <p>Put 6 eq in 5 eq</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-18.webp" alt="DAA Quick sort"> <p>Put n=n-3 in eq 3</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-19.webp" alt="DAA Quick sort"> <p>Put 8 eq in 7 eq</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-20.webp" alt="DAA Quick sort"> <br> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-21.webp" alt="DAA Quick sort"> <p>From 3eq, 5eq, 7eq, 9 eq we get</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-22.webp" alt="DAA Quick sort"> <br> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-23.webp" alt="DAA Quick sort"> <p>From 10 eq</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-24.webp" alt="DAA Quick sort"> <p>Multiply and divide the last term by 2</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-25.webp" alt="DAA Quick sort"> <p> <strong>Is the average case complexity of quick sort for sorting n elements.</strong> </p> <p> <strong>3. Quick Sort [Best Case]:</strong> In any sorting, best case is the only case in which we don't make any comparison between elements that is only done when we have only one element to sort.</p> <img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-26.webp" alt="DAA Quick sort"> <hr></h3></x)>
Deixar 44 ser el Pivot element i escaneig fet de dreta a esquerra
Comparant 44 als elements del costat dret, i si els elements del costat dret ho són més petit que 44 , després intercanvieu-lo. Com 22 és més petit que 44 així que intercanvieu-los.
<strong>22</strong> 33 11 55 77 90 40 60 99 <strong>44</strong> 88
Ara comparant 44 a l'element del costat esquerre i l'element ha de ser més gran de 44 i després intercanvieu-los. Com 55 són més grans que 44 així que intercanvieu-los.
22 33 11 <strong>44</strong> 77 90 40 60 99 <strong>55</strong> 88
Recursivament, repetint els passos 1 i 2 fins que ens queden dues llistes una de l'element pivot 44 & un directament des de l'element pivot.
22 33 11 <strong>40</strong> 77 90 <strong>44</strong> 60 99 55 88
Canvia amb 77:
22 33 11 40 <strong>44</strong> 90 <strong>77</strong> 60 99 55 88
Ara, l'element del costat dret i del costat esquerre són més grans que i més petits que 44 respectivament.
Ara tenim dues llistes ordenades:

I aquestes subllistes s'ordenen sota el mateix procés que s'ha fet anteriorment.
Aquestes dues subllistes ordenades una al costat de l'altra.


Fusió de subllistes:

LLISTES ORDENADES
Anàlisi del pitjor cas: És el cas quan els elements ja estan en forma ordenada i intentem ordenar-los de nou. Això necessitarà molt de temps i espai.
Equació:
T (n) =T(1)+T(n-1)+n
T (1) és el temps que triga l'element pivot.
T (n-1) és el temps que triga l'element restant excepte l'element pivot.
N: el nombre de comparacions necessàries per identificar la posició exacta de si mateix (cada element)
Si comparem el primer element pivot amb un altre, hi haurà 5 comparacions.
Significa que hi haurà n comparacions si hi ha n elements.

Fórmula relacional per al pitjor dels casos:

Nota: per fer T (n-4) com a T (1) posarem (n-1) en lloc de '4' i si
Posem (n-1) en lloc de 4 i després hem de posar (n-2) en lloc de 3 i (n-3)
En lloc de 2 i així successivament.
T(n)=(n-1) T(1) + T(n-(n-1))+(n-(n-2))+(n-(n-3))+(n-( n-4))+n
T (n) = (n-1) T (1) + T (1) + 2 + 3 + 4+...........n
T (n) = (n-1) T (1) +T (1) +2+3+4+...........+n+1-1
[Afegir 1 i restar 1 per fer sèries AP]
T (n) = (n-1) T (1) +T (1) +1+2+3+4+........ + n-1
T (n) = (n-1) T (1) +T (1) +  -1
-1
Condició d'aturada: T (1) =0
Perquè finalment només queda un element i no cal cap comparació.
T (n) = (n-1) (0) +0+  -1
-1

La complexitat del pitjor cas de l'ordenació ràpida és T (n) =O (n 2 )
Classificació ràpida aleatòria [cas mitjana]:
En general, assumim el primer element de la llista com a element pivot. En un cas mitjà, el nombre de possibilitats d'obtenir un element pivot és igual al nombre d'elements.
Let total time taken =T (n) For eg: In a given list p 1, p 2, p 3, p 4............pn If p 1 is the pivot list then we have 2 lists. I.e. T (0) and T (n-1) If p2 is the pivot list then we have 2 lists. I.e. T (1) and T (n-2) p 1, p 2, p 3, p 4............pn If p3 is the pivot list then we have 2 lists. I.e. T (2) and T (n-3) p 1, p 2, p 3, p 4............p n
Així, en general, si prenem el Kth element per ser l'element pivot.
Llavors,

L'element pivot farà una comparació i estem fent un cas mitjà, per tant,

Així que la fórmula relacional per a l'ordenació ràpida aleatòria és:
<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-12.webp" alt="DAA Quick sort"> = n+1 +<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-13.webp" alt="DAA Quick sort">(T(0)+T(1)+T(2)+...T(n-1)+T(n-2)+T(n-3)+...T(0)) <br> = n+1 +<img src="//techcodeview.com/img/daa-tutorial/50/quick-sort-13.webp" alt="DAA Quick sort">x2 (T(0)+T(1)+T(2)+...T(n-2)+T(n-1))
n T (n) = n (n+1) +2 (T(0)+T(1)+T(2)+...T(n-1)........eq 1
Posa n=n-1 a l'equació 1
(n -1) T (n-1) = (n-1) n+2 (T(0)+T(1)+T(2)+...T(n-2)......eq2
De l'eq1 i l'eq 2
n T (n) - (n-1) T (n-1)= n(n+1)-n(n-1)+2 (T(0)+T(1)+T(2)+? T(n-2)+T(n-1))-2(T(0)+T(1)+T(2)+...T(n-2))
n T(n)- (n-1) T(n-1)= n[n+1-n+1]+2T(n-1)
n T(n)=[2+(n-1)]T(n-1)+2n
n T(n)= n+1 T(n-1)+2n

Posa n=n-1 a l'equació 3

Posa 4 eq en 3 eq

Posa n=n-2 a l'equació 3

Posa 6 eq en 5 eq

Posa n=n-3 a l'equació 3

Posa 8 eq en 7 eq


A partir de 3eq, 5eq, 7eq, 9 eq obtenim


A partir de 10 eq

Multiplica i divideix l'últim terme per 2

És la complexitat mitjana del cas de l'ordenació ràpida per ordenar n elements.
3. Classificació ràpida [Millor cas]: En qualsevol classificació, el millor dels casos és l'únic cas en què no fem cap comparació entre elements que només es fa quan només tenim un element per ordenar.