Localització òptima del punt per minimitzar la distància total

 #practiceLinkDiv { mostrar: cap !important; }
#practiceLinkDiv { mostrar: cap !important; } Donat un conjunt de punts com i una recta com ax+by+c = 0. Hem de trobar un punt en una línia donada per al qual la suma de distàncies d'un conjunt de punts donat sigui mínima.
Exemple:

In above figure optimum location of point of x - y - 3 = 0 line is (2 -1) whose total distance with other points is 20.77 which is minimum obtainable total distance.Recommended Practice Localització òptima del punt per minimitzar la distància total Prova-ho!
Si prenem un punt d'una línia donada a una distància infinita, el cost total de la distància serà infinit ara quan movem aquest punt a la línia cap a punts donats, el cost total de la distància comença a disminuir i després d'un temps torna a augmentar, que arriba a l'infinit a l'altre extrem infinit de la línia, de manera que la corba del cost de la distància sembla una corba U i hem de trobar el valor inferior d'aquesta corba U.
Com que la corba U no augmenta ni disminueix monòtonament, no podem utilitzar la cerca binària per trobar el punt més baix aquí farem servir la cerca ternària per trobar el punt més baix la cerca ternària salta un terç de l'espai de cerca a cada iteració, podeu llegir més sobre la cerca ternària aquí .
Així que la solució procedeix de la següent manera, comencem amb els valors baix i alt inicialitzats com a valors més petits i més grans respectivament, després comencem la iteració a cada iteració, calculem dos mitjans mid1 i mid2 que representen 1/3 i 2/3 posicions a l'espai de cerca, calculem la distància total de tots els punts amb mid1 i mid2 i actualitzem baix o alt comparant aquestes distàncies costen aquesta iteració aproximadament.
C++ // C/C++ program to find optimum location and total cost #include using namespace std ; #define sq(x) ((x) * (x)) #define EPS 1e-6 #define N 5 // structure defining a point struct point { int x y ; point () {} point ( int x int y ) : x ( x ) y ( y ) { } }; // structure defining a line of ax + by + c = 0 form struct line { int a b c ; line ( int a int b int c ) : a ( a ) b ( b ) c ( c ) { } }; // method to get distance of point (x y) from point p double dist ( double x double y point p ) { return sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = -1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance double findOptimumCostUtil ( point p [] int n line l ) { double low = -1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x co-ordiantes // of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; // double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost double findOptimumCost ( int points [ N ][ 2 ] line l ) { point p [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver code to test above method int main () { line l ( 1 -1 -3 ); int points [ N ][ 2 ] = { { -3 -2 } { -1 0 } { -1 2 } { 1 2 } { 3 4 } }; cout < < findOptimumCost ( points l ) < < endl ; return 0 ; }
Java // A Java program to find optimum location // and total cost class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point static class point { int x y ; point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line of ax + by + c = 0 form static class line { int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of point (x y) from point p static double dist ( double x double y point p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ static double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ] ); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point p [] int n line l ) { double low = - 1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int points [][] line l ) { point [] p = new point [ N ] ; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ] ); return findOptimumCostUtil ( p N l ); } // Driver Code public static void main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int points [][] = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; System . out . println ( findOptimumCost ( points l )); } } // This code is contributed by Rajput-Ji
Python3 # A Python3 program to find optimum location # and total cost import math class Optimum_distance : # Class defining a point class Point : def __init__ ( self x y ): self . x = x self . y = y # Class defining a line of ax + by + c = 0 form class Line : def __init__ ( self a b c ): self . a = a self . b = b self . c = c # Method to get distance of point # (x y) from point p def dist ( self x y p ): return math . sqrt (( x - p . x ) ** 2 + ( y - p . y ) ** 2 ) # Utility method to compute total distance # all points when choose point on given # line has x-coordinate value as X def compute ( self p n l x ): res = 0 y = - 1 * ( l . a * x + l . c ) / l . b # Calculating Y of chosen point # by line equation for i in range ( n ): res += self . dist ( x y p [ i ]) return res # Utility method to find minimum total distance def find_Optimum_cost_untill ( self p n l ): low = - 1e6 high = 1e6 eps = 1e-6 + 1 # Loop until difference between low # and high become less than EPS while (( high - low ) > eps ): # mid1 and mid2 are representative x # co-ordiantes of search space mid1 = low + ( high - low ) / 3 mid2 = high - ( high - low ) / 3 dist1 = self . compute ( p n l mid1 ) dist2 = self . compute ( p n l mid2 ) # If mid2 point gives more total # distance skip third part if ( dist1 < dist2 ): high = mid2 # If mid1 point gives more total # distance skip first part else : low = mid1 # Compute optimum distance cost by # sending average of low and high as X return self . compute ( p n l ( low + high ) / 2 ) # Method to find optimum cost def find_Optimum_cost ( self p l ): n = len ( p ) p_arr = [ None ] * n # Converting 2D array input to point array for i in range ( n ): p_obj = self . Point ( p [ i ][ 0 ] p [ i ][ 1 ]) p_arr [ i ] = p_obj return self . find_Optimum_cost_untill ( p_arr n l ) # Driver Code if __name__ == '__main__' : obj = Optimum_distance () l = obj . Line ( 1 - 1 - 3 ) p = [ [ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ] ] print ( obj . find_Optimum_cost ( p l )) # This code is contributed by Sulu_mufi
C# // C# program to find optimum location // and total cost using System ; class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point public class point { public int x y ; public point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line // of ax + by + c = 0 form public class line { public int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of // point (x y) from point p static double dist ( double x double y point p ) { return Math . Sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance of all points when choose point on given line has x-coordinate value as X */ static double compute ( point [] p int n line l double X ) { double res = 0 ; // calculating Y of chosen point // by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point [] p int n line l ) { double low = - 1 e6 ; double high = 1 e6 ; // loop until difference between // low and high become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative // x co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by // sending average of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int [ ] points line l ) { point [] p = new point [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i 0 ] points [ i 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code public static void Main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int [ ] points = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; Console . WriteLine ( findOptimumCost ( points l )); } } // This code is contributed by 29AjayKumar
JavaScript < script > // A JavaScript program to find optimum location // and total cost function sq ( x ) { return x * x ; } let EPS = ( 1e-6 ) + 1 ; let N = 5 ; // structure defining a point class point { constructor ( x y ) { this . x = x ; this . y = y ; } } // structure defining a line of ax + by + c = 0 form class line { constructor ( a b c ) { this . a = a ; this . b = b ; this . c = c ; } } // method to get distance of point (x y) from point p function dist ( x y p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ function compute ( p n l X ) { let res = 0 ; // calculating Y of chosen point by line equation let Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( let i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance function findOptimumCostUtil ( p n l ) { let low = - 1e6 ; let high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space let mid1 = low + ( high - low ) / 3 ; let mid2 = high - ( high - low ) / 3 ; let dist1 = compute ( p n l mid1 ); let dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost function findOptimumCost ( points l ) { let p = new Array ( N ); // converting 2D array input to point array for ( let i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code let l = new line ( 1 - 1 - 3 ); let points = [[ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ]]; document . write ( findOptimumCost ( points l )); // This code is contributed by rag2127 < /script>
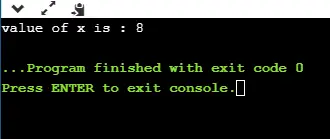
Sortida
20.7652
Complexitat temporal: O (n 2 )
Espai auxiliar: O(n)