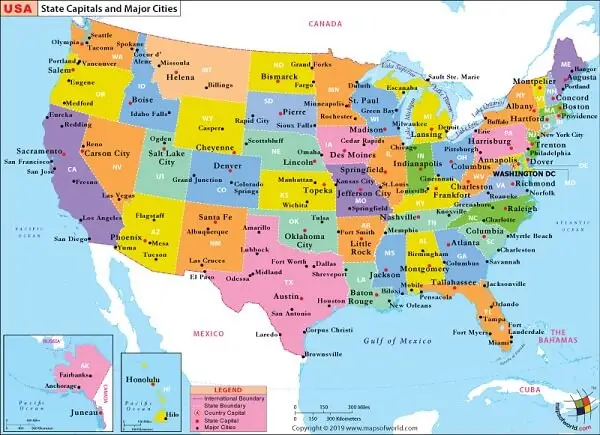
FÒRMULA DE GUANY DE MASON

La relació entre una variable d'entrada i una variable de sortida d'un gràfic de flux de senyal ve donada per la fórmula de guany de Mason.
Per a la determinació del sistema global, el guany ve donat per:

On,
P k = guany de camí cap endavant de la K th camí endavant.
∆ = 1 - [Suma del guany del bucle de tots els bucles individuals] + [Suma dels productes del guany de tots els possibles dos bucles no tàctils] + [Suma dels productes del guany dels tres llaços possibles] + ... ....
∆ k = El valor de ∆ per al camí del gràfic és la part del gràfic que no toca la K th camí endavant.

Camí endavant
A partir de l'SFG anterior, hi ha dos camins cap endavant amb el seu guany de camí com -

Bucle
Hi ha 5 bucles individuals a l'SFG anterior amb el seu guany de bucle com -

Bucles no tàctils
Hi ha dues combinacions possibles del bucle no tàctil amb el producte de guany de bucle com -

A l'SFG anterior, no hi ha combinacions de tres bucles no tàctils, 4 llaços no tàctils, etc.
On,


Exemple
Dibuixeu el diagrama de flux de senyal i determineu C/R per al diagrama de blocs que es mostra a la figura.

A continuació es dibuixa el gràfic de flux de senyal del diagrama anterior

El guany dels camins endavant
P 1 = G 1 G 2 G 3 ∆ 1 = 1
P 2 = -G 1 G 4 ∆ 2 = 1
Bucles individuals
L 1 = - G 1 G 2 H 1
L 2 = -G 2 G 3 H 2
L 3 = -G 1 G 2 G 3
L 4 = G 1 G 4
L 5 = G 4 H 2
Bucles sense tocar = 0