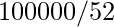Trobar el nombre de dígits en n'èsimo nombre de Fibonacci

 #practiceLinkDiv { mostrar: cap !important; }
#practiceLinkDiv { mostrar: cap !important; } Donat un nombre n, trobeu el nombre de dígits en n'èsimo nombres de Fibonacci. Els primers nombres de Fibonacci són 0 1 1 2 3 5 8 13 21 34 55 89 144 ....
Exemples:
Input : n = 6
Output : 1
6'th Fibonacci number is 8 and it has
1 digit.
Input : n = 12
Output : 3
12'th Fibonacci number is 144 and it has
3 digits.
Pràctica recomanada nè dígit de Fibonacci Prova-ho!
A solució senzilla és trobar n'è número de Fibonacci i després comptar el nombre de dígits que hi ha. Aquesta solució pot provocar problemes de desbordament per a valors grans de n.
A manera directa és comptar el nombre de dígits de l'enèsimo nombre de Fibonacci utilitzant la fórmula de Binet a continuació.
fib(n) = (? n - ? -n ) / ?5
where
? = (1 + ?5) / 2
? = (1 - ?5) / 2
The above formula can be simplified
fib(n) = round(? n / ?5)
Here round function indicates nearest integer.
Count of digits in Fib(n) = Log 10 Fib(n)
= Log 10 (? n / ?5)
= n*Log 10 (?) - Log 10 ?5
= n*Log 10 (?) - (Log 10 5)/2
C++
Com s'esmenta a això G-Fact aquesta fórmula sembla que no funciona i produeix nombres de Fibonacci correctes a causa de les limitacions de l'aritmètica de coma flotant. Tanmateix, sembla viable utilitzar aquesta fórmula per trobar el recompte de dígits en el número n'è de Fibonacci.
A continuació es mostra la implementació de la idea anterior:
Java/* C++ program to find number of digits in nth Fibonacci number */ #includeusing namespace std ; // This function returns the number of digits // in nth Fibonacci number after ceiling it // Formula used (n * log(phi) - (log 5) / 2) long long numberOfDigits ( long long n ) { if ( n == 1 ) return 1 ; // using phi = 1.6180339887498948 long double d = ( n * log10 ( 1.6180339887498948 )) - (( log10 ( 5 )) / 2 ); return ceil ( d ); } // Driver program to test the above function int main () { long long i ; for ( i = 1 ; i <= 10 ; i ++ ) cout < < 'Number of Digits in F(' < < i < < ') - ' < < numberOfDigits ( i ) < < ' n ' ; return 0 ; } Python3// Java program to find number of digits in nth // Fibonacci number class GFG { // This function returns the number of digits // in nth Fibonacci number after ceiling it // Formula used (n * log(phi) - (log 5) / 2) static double numberOfDigits ( double n ) { if ( n == 1 ) return 1 ; // using phi = 1.6180339887498948 double d = ( n * Math . log10 ( 1.6180339887498948 )) - (( Math . log10 ( 5 )) / 2 ); return Math . ceil ( d ); } // Driver code public static void main ( String [] args ) { double i ; for ( i = 1 ; i <= 10 ; i ++ ) System . out . println ( 'Number of Digits in F(' + i + ') - ' + numberOfDigits ( i )); } } // This code is contributed by Anant Agarwal.C## Python program to find # number of digits in nth # Fibonacci number import math # storing value of # golden ratio aka phi phi = ( 1 + 5 ** .5 ) / 2 # function to find number # of digits in F(n) This # function returns the number # of digitsin nth Fibonacci # number after ceiling it # Formula used (n * log(phi) - # (log 5) / 2) def numberOfDig ( n ) : if n == 1 : return 1 return math . ceil (( n * math . log10 ( phi ) - .5 * math . log10 ( 5 ))) // Driver Code for i in range ( 1 11 ) : print ( 'Number of Digits in F(' + str ( i ) + ') - ' + str ( numberOfDig ( i ))) # This code is contributed by SujanDuttaJavaScript// C# program to find number of // digits in nth Fibonacci number using System ; class GFG { // This function returns the number of digits // in nth Fibonacci number after ceiling it // Formula used (n * log(phi) - (log 5) / 2) static double numberOfDigits ( double n ) { if ( n == 1 ) return 1 ; // using phi = 1.6180339887498948 double d = ( n * Math . Log10 ( 1.6180339887498948 )) - (( Math . Log10 ( 5 )) / 2 ); return Math . Ceiling ( d ); } // Driver code public static void Main () { double i ; for ( i = 1 ; i <= 10 ; i ++ ) Console . WriteLine ( 'Number of Digits in F(' + i + ') - ' + numberOfDigits ( i )); } } // This code is contributed by Nitin Mittal.PHP< script > // Javascript program to find number of // digits in nth Fibonacci number // This function returns the // number of digits in nth // Fibonacci number after // ceiling it Formula used // (n * log(phi) - (log 5) / 2) function numberOfDigits ( n ) { if ( n == 1 ) return 1 ; // using phi = 1.6180339887498948 let d = ( n * Math . log10 ( 1.6180339887498948 )) - (( Math . log10 ( 5 )) / 2 ); return Math . ceil ( d ); } // Driver Code let i ; for ( let i = 1 ; i <= 10 ; i ++ ) document . write ( `Number of Digits in F( ${ i } ) - ${ numberOfDigits ( i ) }
` ); // This code is contributed by _saurabh_jaiswal < /script>
SortidaNumber of Digits in F(1) - 1 Number of Digits in F(2) - 1 Number of Digits in F(3) - 1 Number of Digits in F(4) - 1 Number of Digits in F(5) - 1 Number of Digits in F(6) - 1 Number of Digits in F(7) - 2 Number of Digits in F(8) - 2 Number of Digits in F(9) - 2 Number of Digits in F(10) - 2Complexitat temporal: O(1)
Espai auxiliar: O(1)Un altre enfocament (utilitzant el fet que els nombres de Fibonacci són periòdics):
La seqüència de Fibonacci és periòdica mòdul qualsevol nombre enter amb període igual a 60 (conegut com a període de Pisano). Això vol dir que podem calcular l'èsimo nombre de Fibonacci mòdul 10 ^ k per a una k gran i després utilitzar la periodicitat per calcular el nombre de dígits. Per exemple, podem calcular F_n mòdul 10^10 i comptar el nombre de dígits:
F_n_mod = F_n % 10**10
dígits = pis (log10 (F_n_mod)) + 1A continuació es mostra la implementació de l'enfocament anterior:
C++Java#includeusing namespace std ; long long numberOfDigits ( long long n ){ int k = 10 ; // module 10^k int phi = ( 1 + sqrt ( 5 )) / 2 ; //golden ratio // compute the n-th Fibonacci number modulo 10^k int a = 0 b = 1 ; for ( int i = 2 ; i <= n ; i ++ ) { int c = ( a + b ) % int ( pow ( 10 k )); a = b ; b = c ; } int F_n_mod = b ; // compute the number of digits in F_n_mod int digits = 1 ; while ( F_n_mod >= 10 ) { F_n_mod /= 10 ; digits ++ ; } return digits ; } int main (){ long long i ; for ( i = 1 ; i <= 10 ; i ++ ) cout < < 'Number of Digits in F(' < < i < < ') - ' < < numberOfDigits ( i ) < < ' n ' ; return 0 ; } // This code is contributed by Yash Agarwal(yashagarwal2852002) Python3import java.util.* ; public class GFG { public static long numberOfDigits ( long n ) { int k = 10 ; // module 10^k double phi = ( 1 + Math . sqrt ( 5 )) / 2 ; //golden ratio // compute the n-th Fibonacci number modulo 10^k int a = 0 b = 1 ; for ( int i = 2 ; i <= n ; i ++ ) { int c = ( a + b ) % ( int ) Math . pow ( 10 k ); a = b ; b = c ; } int F_n_mod = b ; // compute the number of digits in F_n_mod int digits = 1 ; while ( F_n_mod >= 10 ) { F_n_mod /= 10 ; digits ++ ; } return digits ; } public static void main ( String [] args ) { long i ; for ( i = 1 ; i <= 10 ; i ++ ) System . out . println ( 'Number of Digits in F(' + i + ') - ' + numberOfDigits ( i )); } }C#import math def numberOfDigits ( n ): k = 10 # Golden ratio (approximately 1.618033988749895) phi = ( 1 + math . sqrt ( 5 )) / 2 # Compute the n-th Fibonacci number modulo 10^k a b = 0 1 # Start the loop from 2 as we already have F(0) and F(1) for i in range ( 2 n + 1 ): c = ( a + b ) % pow ( 10 k ) # Update the previous Fibonacci numbers for the next iteration a = b b = c F_n_mod = b # Compute the number of digits in F_n_mod # Initialize the digit counter to 1 (as any number has at least one digit) digits = 1 # Keep dividing F_n_mod by 10 until it becomes less than 10 while F_n_mod >= 10 : F_n_mod = F_n_mod // 10 # Increment the digit counter digits += 1 # Return the number of digits in the n-th Fibonacci number modulo 10^k return digits # Driver code for i in range ( 1 11 ): # Calculate and print the number of digits in F(i) modulo 10^10 print ( 'Number of Digits in F(' + str ( i ) + ') - ' + str ( numberOfDigits ( i ))) # THIS CODE IS CONTRIBUTED BY YASH AGARWAL(YASHAGARWAL2852002)JavaScriptusing System ; class GFG { static int NumberOfDigits ( long n ) { int k = 10 ; // modulo 10^k // Compute the n-th Fibonacci number modulo 10^k int a = 0 b = 1 ; for ( int i = 2 ; i <= n ; i ++ ) { int c = ( a + b ) % ( int ) Math . Pow ( 10 k ); a = b ; b = c ; } int F_n_mod = b ; // Compute the number of digits in F_n_mod int digits = 1 ; while ( F_n_mod >= 10 ) { F_n_mod /= 10 ; digits ++ ; } return digits ; } static void Main ( string [] args ) { for ( long i = 1 ; i <= 10 ; i ++ ) { Console . WriteLine ( $'Number of Digits in F({i}) - {NumberOfDigits(i)}' ); } } }
SortidaNumber of Digits in F(1) - 1 Number of Digits in F(2) - 1 Number of Digits in F(3) - 1 Number of Digits in F(4) - 1 Number of Digits in F(5) - 1 Number of Digits in F(6) - 1 Number of Digits in F(7) - 2 Number of Digits in F(8) - 2 Number of Digits in F(9) - 2 Number of Digits in F(10) - 2Complexitat temporal: O(nk)
Espai auxiliar: O(1)
Referències:
https://r-knott.surrey.ac.uk/Fibonacci/fibFormula.html#section2
https://en.wikipedia.org/wiki/Fibonacci_number