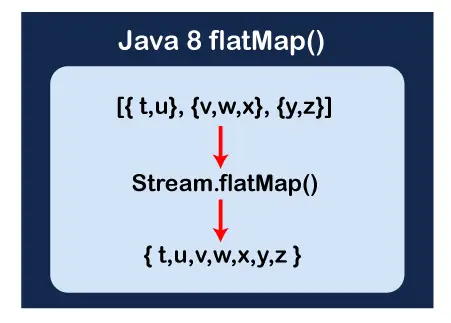
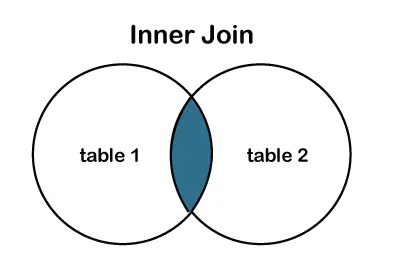
Algoritme d'encaminament vectorial de distància
- L'algorisme del vector de distància és un algorisme dinàmic.
- S'utilitza principalment en ARPANET i RIP.
- Cada encaminador manté una taula de distàncies coneguda com a Vector .
Tres claus per entendre el funcionament de l'algoritme d'encaminament vectorial a distància:
Algoritme d'encaminament vectorial de distància
Sigui d x (y) sigui el cost del camí de menor cost del node x al node y. Els menors costos estan relacionats per l'equació de Bellman-Ford,
d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} On el minv és l'equació presa per a tots els x veïns. Després de viatjar de x a v, si considerem el camí de menor cost de v a y, el cost del camí serà c(x,v)+d en (y). El menor cost de x a y és el mínim de c(x,v)+d en (y) es va fer càrrec de tots els veïns.
Amb l'algorisme d'encaminament del vector de distància, el node x conté la informació d'encaminament següent:
- Per a cada veí v, el cost c(x,v) és el cost del camí des de x fins al veí connectat directament, v.
- El vector distància x, és a dir, D x = [ D x (y): y en N ], que inclou el seu cost a totes les destinacions, y, en N.
- El vector distància de cadascun dels seus veïns, és a dir, D en = [ D en (y): y en N ] per a cada veí v de x.
L'encaminament del vector de distància és un algorisme asíncron en el qual el node x envia la còpia del seu vector de distància a tots els seus veïns. Quan el node x rep el nou vector de distància d'un dels seus vectors veí, v, desa el vector de distància de v i utilitza l'equació de Bellman-Ford per actualitzar el seu propi vector de distància. L'equació es dóna a continuació:
d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N El node x ha actualitzat la seva pròpia taula de vectors de distància utilitzant l'equació anterior i envia la seva taula actualitzada a tots els seus veïns perquè puguin actualitzar els seus propis vectors de distància.
Algorisme
At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = ∞ for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> Nota: a l'algorisme de vector de distància, el node x actualitza la seva taula quan veu qualsevol canvi de cost en un node directament enllaçat o rep una actualització vectorial d'algun veí.
Entenem-ho a través d'un exemple:
Compartint informació

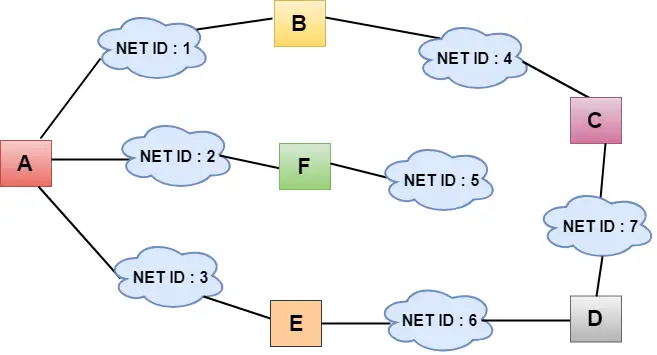
- A la figura anterior, cada núvol representa la xarxa i el número dins del núvol representa l'ID de la xarxa.
- Totes les LAN estan connectades per encaminadors i es representen en quadres etiquetats com A, B, C, D, E, F.
- L'algorisme d'encaminament de vectors de distància simplifica el procés d'encaminament suposant que el cost de cada enllaç és d'una unitat. Per tant, l'eficiència de la transmissió es pot mesurar pel nombre d'enllaços per arribar a la destinació.
- A l'encaminament vectorial de distància, el cost es basa en el recompte de salts.

A la figura anterior, observem que l'encaminador envia el coneixement als veïns immediats. Els veïns afegeixen aquests coneixements al seu propi coneixement i envia la taula actualitzada als seus propis veïns. D'aquesta manera, els routers obtenen la seva pròpia informació més la nova informació sobre els veïns.
Taula d'encaminament
Es produeixen dos processos:
- Creació de la Taula
- Actualització de la taula
Creació de la Taula
Inicialment, es crea la taula d'encaminament per a cada encaminador que conté almenys tres tipus d'informació, com ara l'identificador de xarxa, el cost i el salt següent.


- A la figura anterior, es mostren les taules d'encaminament originals de tots els encaminadors. En una taula d'encaminament, la primera columna representa l'ID de la xarxa, la segona columna representa el cost de l'enllaç i la tercera columna està buida.
- Aquestes taules d'encaminament s'envien a tots els veïns.
Per exemple:
A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A.
Actualització de la taula
- Quan A rep una taula d'encaminament de B, utilitza la seva informació per actualitzar la taula.
- La taula d'encaminament de B mostra com es poden moure els paquets a les xarxes 1 i 4.
- El B és un veí del router A, els paquets d'A a B poden arribar en un sol salt. Així, s'afegeix 1 a tots els costos indicats a la taula de B i la suma serà el cost per arribar a una xarxa determinada.

- Després de l'ajust, A combina aquesta taula amb la seva pròpia taula per crear una taula combinada.

- La taula combinada pot contenir algunes dades duplicades. A la figura anterior, la taula combinada de l'encaminador A conté les dades duplicades, de manera que només conserva aquelles dades que tenen el cost més baix. Per exemple, A pot enviar les dades a la xarxa 1 de dues maneres. El primer, que no utilitza cap encaminador següent, de manera que costa un salt. El segon requereix dos salts (A a B, després B a la xarxa 1). La primera opció té el cost més baix, per tant es manté i la segona s'abandona.

- El procés de creació de la taula d'encaminament continua per a tots els encaminadors. Cada router rep la informació dels veïns i actualitza la taula d'encaminament.
Les taules d'encaminament finals de tots els encaminadors es donen a continuació: