L'algorithme de multiplication de Booth

L'algorithme de Booth est un algorithme de multiplication qui nous permet de multiplier respectivement deux entiers binaires signés en complément de 2. Il est également utilisé pour accélérer les performances du processus de multiplication. C'est très efficace aussi. Il fonctionne sur les bits de chaîne 0 dans le multiplicateur qui ne nécessite aucun bit supplémentaire, il suffit de décaler les bits de chaîne les plus à droite et une chaîne de 1 dans un poids de bits multiplicateur 2. k au poids 2 m que l'on peut considérer comme 2 k+1 - 2 m .
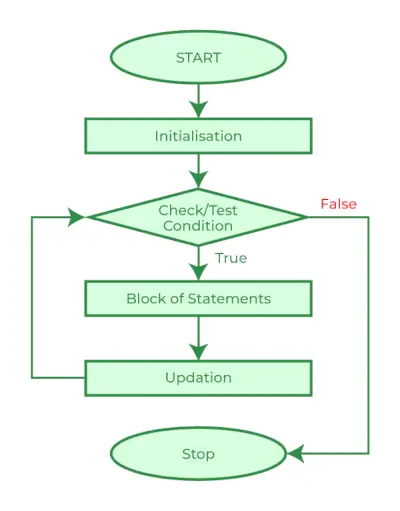
Voici la représentation picturale de l'algorithme de Booth :

Dans l'organigramme ci-dessus, initialement, CA et Q n + 1 les bits sont mis à 0 et les CS est un compteur de séquence qui représente le total des bits définis n, qui est égal au nombre de bits du multiplicateur. Il y a BR qui représentent le bits multiplicandes, et QR représente le bits multiplicateurs . Après cela, nous avons rencontré deux bits du multiplicateur comme Q n et Q n + 1 , où Qn représente le dernier bit de QR, et Q n + 1 représente le bit incrémenté de Qn de 1. Supposons que deux bits du multiplicateur soient égaux à 10 ; cela signifie que nous devons soustraire le multiplicateur du produit partiel dans l'accumulateur AC puis effectuer l'opération de décalage arithmétique (ashr). Si les deux multiplicateurs sont égaux à 01, cela signifie que nous devons effectuer l'addition du multiplicande au produit partiel dans l'accumulateur AC puis effectuer l'opération de décalage arithmétique ( Ashr ), y compris Q n + 1 . L'opération de décalage arithmétique est utilisée dans l'algorithme de Booth pour décaler les bits AC et QR d'un vers la droite et reste le bit de signe dans AC inchangé. Et le compteur de séquence est continuellement décrémenté jusqu'à ce que la boucle de calcul soit répétée, égale au nombre de bits (n).
Travailler sur l'algorithme du stand
- Définissez les bits binaires multiplicande et multiplicateur sur M et Q, respectivement.
- Initialement, nous définissons l'AC et le Q n + 1 enregistre la valeur à 0.
- SC représente le nombre de bits multiplicateurs (Q), et c'est un compteur de séquence qui est continuellement décrémenté jusqu'à être égal au nombre de bits (n) ou atteint 0.
- Un Qn représente le dernier bit du Q, et le Q n+1 montre le bit incrémenté de Qn de 1.
- À chaque cycle de l'algorithme de stand, Q n et Q n + 1 les bits seront vérifiés sur les paramètres suivants comme suit :
- Quand deux bits Q n et Q n + 1 sont 00 ou 11, nous effectuons simplement l’opération de décalage arithmétique vers la droite (ashr) vers le produit partiel AC. Et les bits de Qn et Q n + 1 est incrémenté de 1 bit.
- Si les bits de Q n et Q n + 1 s'affiche à 01, les bits multiplicandes (M) seront ajoutés à l'AC (registre accumulateur). Après cela, nous effectuons l'opération de décalage à droite vers les bits AC et QR de 1.
- Si les bits de Q n et Q n + 1 est affiché à 10, les bits multiplicandes (M) seront soustraits de l'AC (registre accumulateur). Après cela, nous effectuons l'opération de décalage à droite vers les bits AC et QR de 1.
- L'opération fonctionne en continu jusqu'à ce que nous atteignions n - 1 bit dans l'algorithme du stand.
- Les résultats des bits binaires de multiplication seront stockés dans les registres AC et QR.
Deux méthodes sont utilisées dans l'algorithme de Booth :
1. RSC (circulaire de décalage à droite)
Il décale le bit le plus à droite du nombre binaire, puis il est ajouté au début des bits binaires.

2. RSA (arithmétique du décalage vers la droite)
Il ajoute les deux bits binaires, puis décale le résultat vers la droite d'une position de 1 bit.
Exemple : 0100 + 0110 => 1010, après avoir ajouté le nombre binaire, décalez chaque bit de 1 vers la droite et placez le premier bit de la résultante au début du nouveau bit.
Exemple : Multipliez les deux nombres 7 et 3 en utilisant l'algorithme de multiplication de Booth.
Ans . Ici, nous avons deux nombres, 7 et 3. Tout d’abord, nous devons convertir 7 et 3 en nombres binaires comme 7 = (0111) et 3 = (0011). Définissez maintenant 7 (en binaire 0111) comme multiplicande (M) et 3 (en binaire 0011) comme multiplicateur (Q). Et SC (Sequence Count) représente le nombre de bits, et ici nous avons 4 bits, donc définissez SC = 4. En outre, il affiche le nombre de cycles d'itération des algorithmes de la cabine, puis les cycles exécutés SC = SC - 1 fois.
| Q n | Q n + 1 | M = (0111) M' + 1 = (1001) & Opération | CA | Q | Q n + 1 | CS |
|---|---|---|---|---|---|---|
| 1 | 0 | Initial | 0000 | 0011 | 0 | 4 |
| Soustraire (M' + 1) | 1001 | |||||
| 1001 | ||||||
| Effectuer des opérations arithmétiques de décalage vers la droite (ashr) | 1100 | 1001 | 1 | 3 | ||
| 1 | 1 | Effectuer des opérations arithmétiques de décalage vers la droite (ashr) | 1110 | 0100 | 1 | 2 |
| 0 | 1 | Ajout (A + M) | 0111 | |||
| 0101 | 0100 | |||||
| Effectuer une opération de décalage arithmétique vers la droite | 0010 | 1010 | 0 | 1 | ||
| 0 | 0 | Effectuer une opération de décalage arithmétique vers la droite | 0001 | 0101 | 0 | 0 |
L'exemple numérique de l'algorithme de multiplication de Booth est 7 x 3 = 21 et la représentation binaire de 21 est 10101. Ici, nous obtenons le résultat en binaire 00010101. Maintenant, nous le convertissons en décimal, comme (000010101) dix = 2*4 + 2*3 + 2*2 + 2*1 + 2*0 => 21.
Exemple : Multipliez les deux nombres 23 et -9 en utilisant l'algorithme de multiplication de Booth.
Ici, M = 23 = (010111) et Q = -9 = (110111)
| Q n Q n + 1 | M = 0 1 0 1 1 1 M' + 1 = 1 0 1 0 0 1 | CA | Q | Q n + 1 CS |
|---|---|---|---|---|
| Initialement | 000000 | 110111 | 0 6 | |
| dix | Soustraire M | 101001 | ||
| 101001 | ||||
| Effectuer une opération de décalage arithmétique vers la droite | 110100 | 111011 | quinze | |
| onze | Effectuer une opération de décalage arithmétique vers la droite | 111010 | 011101 | 1 4 |
| onze | Effectuer une opération de décalage arithmétique vers la droite | 111101 | 001110 | 1 3 |
| 0 1 | Ajout (A + M) | 010111 | ||
| 010100 | ||||
| Effectuer une opération de décalage arithmétique vers la droite | 001010 | 000111 | 0 2 | |
| dix | Soustraire M | 101001 | ||
| 110011 | ||||
| Effectuer une opération de décalage arithmétique vers la droite | 111001 | 100011 | onze | |
| onze | Effectuer une opération de décalage arithmétique vers la droite | 111100 | 110001 | 1 0 |
Q n + 1 = 1, cela signifie que la sortie est négative.
Donc 23 * -9 = complément à 2 de 111100110001 => (00001100111)