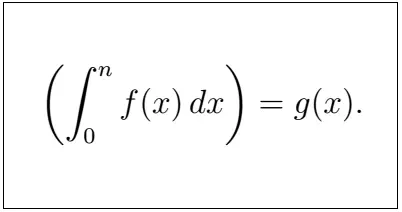Внедряване на афинен шифър

Афинният шифър е вид моноазбучен заместващ шифър, при който всяка буква в азбука се съпоставя с нейния цифров еквивалент, шифрован с помощта на проста математическа функция и преобразуван обратно в буква. Използваната формула означава, че всяка буква криптира една друга буква и обратно, което означава, че шифърът е по същество стандартен заместващ шифър с правило, управляващо коя буква към коя отива.
Целият процес разчита на работен модул m (дължината на използваната азбука). В афинния шифър буквите от азбука с размер m първо се съпоставят с цели числа в диапазона 0 … m-1.
„Ключът“ за афинния шифър се състои от 2 числа, които ще наречем a и b. Следващата дискусия предполага използването на азбука от 26 знака (m = 26). a трябва да бъде избрано да бъде относително просто спрямо m (т.е. a не трябва да има общи фактори с m).

Шифроване
Той използва модулна аритметика, за да преобразува цялото число, на което съответства всяка буква в обикновен текст, в друго цяло число, което съответства на буква в шифрован текст. Функцията за криптиране на една буква е
E ( x ) = ( a x + b ) mod m modulus m: size of the alphabet a and b: key of the cipher. a must be chosen such that a and m are coprime.
Декриптиране
При дешифрирането на шифрования текст трябва да изпълним противоположни (или обратни) функции върху шифрования текст, за да извлечем открития текст. Отново първата стъпка е да конвертирате всяка от буквите на шифрования текст в техните цели числа. Функцията за дешифриране е
D ( x ) = a^-1 ( x - b ) mod m a^-1 : modular multiplicative inverse of a modulo m. i.e. it satisfies the equation 1 = a a^-1 mod m .
За намиране на мултипликативно обратно
Трябва да намерим число x, така че:
Ако намерим числото x, така че уравнението да е вярно, тогава x е обратното на a и го наричаме a^-1. Най-лесният начин да решите това уравнение е да потърсите всяко от числата от 1 до 25 и да видите кое отговаря на уравнението.
[gxd] = gcd(am); % we can ignore g and d we dont need them x = mod(xm);
Ако сега умножите x и a и намалите резултата (mod 26), ще получите отговор 1. Не забравяйте, че това е само дефиницията на обратна, т.е. ако a*x = 1 (mod 26), тогава x е обратна на a (и a е обратна на x)
Пример:

Изпълнение:
C++ //CPP program to illustrate Affine Cipher #include using namespace std ; //Key values of a and b const int a = 17 ; const int b = 20 ; string encryptMessage ( string msg ) { ///Cipher Text initially empty string cipher = '' ; for ( int i = 0 ; i < msg . length (); i ++ ) { // Avoid space to be encrypted if ( msg [ i ] != ' ' ) /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' ) ) + b ) % 26 ) + 'A' ); else //else simply append space character cipher += msg [ i ]; } return cipher ; } string decryptCipher ( string cipher ) { string msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; //Check if (a*i)%26 == 1 //then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . length (); i ++ ) { if ( cipher [ i ] != ' ' ) /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ msg = msg + ( char ) ((( a_inv * (( cipher [ i ] + 'A' - b )) % 26 )) + 'A' ); else //else simply append space character msg += cipher [ i ]; } return msg ; } //Driver Program int main ( void ) { string msg = 'AFFINE CIPHER' ; //Calling encryption function string cipherText = encryptMessage ( msg ); cout < < 'Encrypted Message is : ' < < cipherText < < endl ; //Calling Decryption function cout < < 'Decrypted Message is: ' < < decryptCipher ( cipherText ); return 0 ; }
Java // Java program to illustrate Affine Cipher class GFG { // Key values of a and b static int a = 17 ; static int b = 20 ; static String encryptMessage ( char [] msg ) { /// Cipher Text initially empty String cipher = '' ; for ( int i = 0 ; i < msg . length ; i ++ ) { // Avoid space to be encrypted /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ if ( msg [ i ] != ' ' ) { cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' )) + b ) % 26 ) + 'A' ); } else // else simply append space character { cipher += msg [ i ] ; } } return cipher ; } static String decryptCipher ( String cipher ) { String msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; // Check if (a*i)%26 == 1 // then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . length (); i ++ ) { /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ if ( cipher . charAt ( i ) != ' ' ) { msg = msg + ( char ) ((( a_inv * (( cipher . charAt ( i ) + 'A' - b )) % 26 )) + 'A' ); } else //else simply append space character { msg += cipher . charAt ( i ); } } return msg ; } // Driver code public static void main ( String [] args ) { String msg = 'AFFINE CIPHER' ; // Calling encryption function String cipherText = encryptMessage ( msg . toCharArray ()); System . out . println ( 'Encrypted Message is : ' + cipherText ); // Calling Decryption function System . out . println ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); } } // This code contributed by Rajput-Ji
Python # Implementation of Affine Cipher in Python # Extended Euclidean Algorithm for finding modular inverse # eg: modinv(7 26) = 15 def egcd ( a b ): x y u v = 0 1 1 0 while a != 0 : q r = b // a b % a m n = x - u * q y - v * q b a x y u v = a r u v m n gcd = b return gcd x y def modinv ( a m ): gcd x y = egcd ( a m ) if gcd != 1 : return None # modular inverse does not exist else : return x % m # affine cipher encryption function # returns the cipher text def affine_encrypt ( text key ): ''' C = (a*P + b) % 26 ''' return '' . join ([ chr ((( key [ 0 ] * ( ord ( t ) - ord ( 'A' )) + key [ 1 ] ) % 26 ) + ord ( 'A' )) for t in text . upper () . replace ( ' ' '' ) ]) # affine cipher decryption function # returns original text def affine_decrypt ( cipher key ): ''' P = (a^-1 * (C - b)) % 26 ''' return '' . join ([ chr ((( modinv ( key [ 0 ] 26 ) * ( ord ( c ) - ord ( 'A' ) - key [ 1 ])) % 26 ) + ord ( 'A' )) for c in cipher ]) # Driver Code to test the above functions def main (): # declaring text and key text = 'AFFINE CIPHER' key = [ 17 20 ] # calling encryption function affine_encrypted_text = affine_encrypt ( text key ) print ( 'Encrypted Text: {} ' . format ( affine_encrypted_text )) # calling decryption function print ( 'Decrypted Text: {} ' . format ( affine_decrypt ( affine_encrypted_text key ) )) if __name__ == '__main__' : main () # This code is contributed by # Bhushan Borole
C# // C# program to illustrate Affine Cipher using System ; class GFG { // Key values of a and b static int a = 17 ; static int b = 20 ; static String encryptMessage ( char [] msg ) { /// Cipher Text initially empty String cipher = '' ; for ( int i = 0 ; i < msg . Length ; i ++ ) { // Avoid space to be encrypted /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ if ( msg [ i ] != ' ' ) { cipher = cipher + ( char ) (((( a * ( msg [ i ] - 'A' )) + b ) % 26 ) + 'A' ); } else // else simply append space character { cipher += msg [ i ]; } } return cipher ; } static String decryptCipher ( String cipher ) { String msg = '' ; int a_inv = 0 ; int flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( int i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; // Check if (a*i)%26 == 1 // then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( int i = 0 ; i < cipher . Length ; i ++ ) { /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ if ( cipher [ i ] != ' ' ) { msg = msg + ( char ) ((( a_inv * (( cipher [ i ] + 'A' - b )) % 26 )) + 'A' ); } else //else simply append space character { msg += cipher [ i ]; } } return msg ; } // Driver code public static void Main ( String [] args ) { String msg = 'AFFINE CIPHER' ; // Calling encryption function String cipherText = encryptMessage ( msg . ToCharArray ()); Console . WriteLine ( 'Encrypted Message is : ' + cipherText ); // Calling Decryption function Console . WriteLine ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); } } /* This code contributed by PrinciRaj1992 */
JavaScript //Javascript program to illustrate Affine Cipher //Key values of a and b let a = 17 ; let b = 20 ; function encryptMessage ( msg ) { ///Cipher Text initially empty let cipher = '' ; for ( let i = 0 ; i < msg . length ; i ++ ) { // Avoid space to be encrypted if ( msg [ i ] != ' ' ) /* applying encryption formula ( a x + b ) mod m {here x is msg[i] and m is 26} and added 'A' to bring it in range of ascii alphabet[ 65-90 | A-Z ] */ cipher = cipher + String . fromCharCode (((( a * ( msg [ i ]. charCodeAt ( 0 ) - 65 ) ) + b ) % 26 ) + 65 ); else //else simply append space character cipher += msg [ i ]; } return cipher ; } function decryptCipher ( cipher ) { let msg = '' ; let a_inv = 0 ; let flag = 0 ; //Find a^-1 (the multiplicative inverse of a //in the group of integers modulo m.) for ( let i = 0 ; i < 26 ; i ++ ) { flag = ( a * i ) % 26 ; //Check if (a*i)%26 == 1 //then i will be the multiplicative inverse of a if ( flag == 1 ) { a_inv = i ; } } for ( let i = 0 ; i < cipher . length ; i ++ ) { if ( cipher [ i ] != ' ' ) /*Applying decryption formula a^-1 ( x - b ) mod m {here x is cipher[i] and m is 26} and added 'A' to bring it in range of ASCII alphabet[ 65-90 | A-Z ] */ msg = msg + String . fromCharCode ((( a_inv * (( cipher [ i ]. charCodeAt ( 0 ) + 65 - b )) % 26 )) + 65 ); else //else simply append space character msg += cipher [ i ]; } return msg ; } //Driver Program let msg = 'AFFINE CIPHER' ; //Calling encryption function let cipherText = encryptMessage ( msg ); console . log ( 'Encrypted Message is : ' + cipherText ); //Calling Decryption function console . log ( 'Decrypted Message is: ' + decryptCipher ( cipherText )); // The code is contributed by Arushi Jindal.
Изход
Encrypted Message is : UBBAHK CAPJKX Decrypted Message is: AFFINE CIPHER
Създаване на тест