Декодер

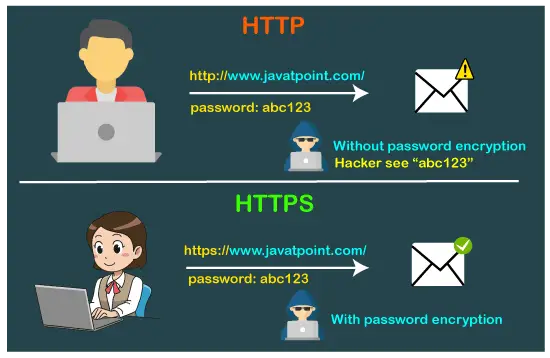
Комбинационната схема, която променя двоичната информация в 2 н изходните линии е известен като Декодери. Двоичната информация се предава под формата на N входни реда. Изходните линии определят 2 н -битов код за двоичната информация. С прости думи, Декодер извършва обратната операция на Енкодер . В даден момент само един входен ред се активира за простота. Произведените 2 н -битов изходен код е еквивалентен на двоичната информация.

Има различни видове декодери, които са както следва:
2 до 4 редов декодер:
В 2 до 4 редовия декодер има общо три входа, т.е. A 0 и А 1 и E и четири изхода, т.е. Y 0 , И 1 , И 2 , и Y 3 . За всяка комбинация от входове, когато активирането 'E' е зададено на 1, един от тези четири изхода ще бъде 1. Блоковата диаграма и таблицата на истината на декодера от 2 до 4 реда са дадени по-долу.
Блокова диаграма:

Таблица на истината:

Логическият израз на термина Y0, Y0, Y2 и Y3 е както следва:
И 3 =E.A 1 .А 0
И 2 =E.A 1 .А 0 '
И 1 =E.A 1 '.A 0
Y0=E.A 1 '.A 0 '
Логическата верига на горните изрази е дадена по-долу:

3 до 8 редов декодер:
Декодерът от 3 до 8 линии е известен още като Двоичен към осмичен декодер . В 3 до 8 редовия декодер има общо осем изхода, т.е. Y 0 , И 1 , И 2 , И 3 , И 4 , И 5 , И 6 , и Y 7 и три изхода, т.е. A 0 , A1 и A 2 . Тази схема има вход за разрешаване 'E'. Точно както при 2 до 4 редовия декодер, когато активирането на 'E' е зададено на 1, един от тези четири изхода ще бъде 1. Блоковата диаграма и таблицата на истинността на 3 до 8 редовия енкодер са дадени по-долу.
Блокова диаграма:

Таблица на истината:

Логическият израз на термина Y 0 , И 1 , И 2 , И 3 , И 4 , И 5 , И 6 , и Y 7 е както следва:
И 0 =А 0 '.A 1 '.A 2 '
И 1 =А 0 .А 1 '.A 2 '
И 2 =А 0 '.A 1 .А 2 '
И 3 =А 0 .А 1 .А 2 '
И 4 =А 0 '.A 1 '.A 2
И 5 =А 0 .А 1 '.A 2
И 6 =А 0 '.A 1 .А 2
И 7 =А 0 .А 1 .А 2
Логическата верига на горните изрази е дадена по-долу:

4 до 16 редов декодер
В 4 до 16 редовия декодер има общо 16 изхода, т.е. Y 0 , И 1 , И 2 ,……, И 16 и четири входа, т.е. A 0 , A1, A 2 и А 3 . Декодерът от 3 до 16 линии може да бъде конструиран с помощта на декодер от 2 до 4 или декодер от 3 до 8. Има следната формула, използвана за намиране на необходимия брой декодери от по-нисък ред.
Необходим брой декодери от по-нисък ред=m 2 /м 1
м 1 = 8
м 2 = 16
Необходим брой от 3 до 8 декодера=  =2
=2
Блокова диаграма:

Таблица на истината:

Логическият израз на термина A0, A1, A2,…, A15 е както следва:
И 0 =А 0 '.A 1 '.A 2 '.A 3 '
И 1 =А 0 '.A 1 '.A 2 '.A 3
И 2 =А 0 '.A 1 '.A 2 .А 3 '
И 3 =А 0 '.A 1 '.A 2 .А 3
И 4 =А 0 '.A 1 .А 2 '.A 3 '
И 5 =А 0 '.A 1 .А 2 '.A 3
И 6 =А 0 '.A 1 .А 2 .А 3 '
И 7 =А 0 '.A 1 .А 2 .А 3
И 8 =А 0 .А 1 '.A 2 '.A 3 '
И 9 =А 0 .А 1 '.A 2 '.A 3
И 10 =А 0 .А 1 '.A 2 .А 3 '
И единадесет =А 0 .А 1 '.A 2 .А 3
И 12 =А 0 .А 1 .А 2 '.A 3 '
И 13 =А 0 .А 1 .А 2 '.A 3
И 14 =А 0 .А 1 .А 2 .А 3 '
И петнадесет =А 0 .А 1 .А 2 '.A 3
Логическата верига на горните изрази е дадена по-долу: