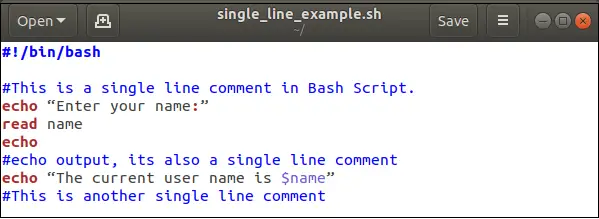
المشابك:

لتكن L مجموعة غير فارغة مغلقة تحت عمليتين ثنائيتين تسمى الالتقاء والانضمام، ويشار إليهما بـ ∧ و ∨. ثم يُطلق على L اسم شبكة إذا كانت البديهيات التالية تثبت أن a، b، c عبارة عن عناصر في L:
1) القانون التبادلي :-
(أ) أ ∧ ب = ب ∧ أ (ب) أ ∨ ب = ب ∨ أ
2) القانون النقابي:-
(أ) (أ ∧ ب)∧ ج = أ ∧(ب∧ ج) (ب) (أ ∨ ب) ∨ ج = أ ∨ (ب ∨ ج)
3) قانون الامتصاص :-
(أ) أ ∧ ( أ ∨ ب) = أ (ب) أ ∨ ( أ ∧ ب) = أ
الازدواجية:
يتم تعريف ثنائي أي عبارة في الشبكة (L,∧ ,∨ ) على أنها عبارة يتم الحصول عليها عن طريق تبادل ∧ و ∨.
على سبيل المثال , ثنائي أ ∧ (ب ∨ أ) = أ ∨ أ هو ∨ (ب ∧ أ )= أ ∧ أ
المشابك يحدها:
تسمى الشبكة L بالشبكة المحدودة إذا كانت تحتوي على العنصر الأكبر 1 والعنصر الأصغر 0.
مثال:
- مجموعة القدرة P(S) للمجموعة S تحت عمليات التقاطع والاتحاد هي شبكة محدودة لأن ∅ هو العنصر الأصغر في P(S) والمجموعة S هي العنصر الأكبر في P(S).
- مجموعة + ve عدد صحيح I + تحت الترتيب المعتاد لـ ≦ ليست شبكة محدودة نظرًا لأنها تحتوي على العنصر الأدنى 1 ولكن العنصر الأكبر غير موجود.
خصائص المشابك المحدودة:
إذا كانت L عبارة عن شبكة محددة، فبالنسبة لأي عنصر a ∈ L، لدينا المتطابقات التالية:
- أ ∨ 1 = 1
- أ ∧1= أ
- أ ∨0 = أ
- أ ∧0=0
نظرية: أثبت أن كل شبكة محدودة L = {a 1 ،أ 2 ،أ 3 ....أ ن } يحدها.
دليل: لقد أعطينا الشبكة المحدودة:
ل = {أ 1 ،أ 2 ،أ 3 ....أ ن }
وبالتالي، فإن العنصر الأعظم في المشابك L هو أ 1 ∨ أ 2 ∨ أ 3∨....∨أ ن .
كما أن أقل عنصر في الشبكة L هو أ 1 ∧ أ 2 ∧أ 3 ∧....∧أ ن .
وبما أن العناصر الأكبر والأصغر موجودة في كل شبكة محدودة. ومن ثم، يحدها L.
الشبكات الفرعية:
النظر في مجموعة فرعية غير فارغة L 1 من شعرية L. ثم L 1 يُطلق عليها شبكة فرعية من L إذا كانت L 1 في حد ذاته عبارة عن شبكة، أي عملية L أي a ∨ b ∈ L 1 و ∧ ب ∈ L 1 عندما يكون ∈ L 1 و ب ∈ L 1 .
مثال: النظر في شعرية جميع الأعداد الصحيحة + ve I + تحت عملية القسمة. الشباك د ن جميع مقسومات n > 1 عبارة عن شبكة فرعية من I + .
تحديد جميع الشبكات الفرعية لـ D 30 التي تحتوي على أربعة عناصر على الأقل، د 30 ={1,2,3,5,6,10,15,30}.
حل: الشبكات الفرعية د 30 التي تحتوي على أربعة عناصر على الأقل وهي كما يلي:
1. {1، 2، 6، 30} 2. {1، 2، 3، 30}
3. {1، 5، 15، 30} 4. {1، 3، 6، 30}
5. {1، 5، 10، 30} 6. {1، 3، 15، 30}
7. {2، 6، 10، 30}
المشابك متماثلة:
شبكتان L 1 و أنا 2 تسمى شبكات متماثلة إذا كان هناك انحراف من L 1 إلى ل 2 أي، و: ل 1 ⟶ ل 2 ، بحيث f (a ∧ b) =f(a)∧ f(b) و f (a ∨ b) = f (a) ∨ f (b)
مثال: حدد ما إذا كانت الشبكات الموضحة في الشكل متماثلة أم لا.
حل: المشابك الموضحة في الشكل متماثلة الشكل. خذ بعين الاعتبار التعيين f = {(a, 1), (b, 2), (c, 3), (d, 4)}. على سبيل المثال f (b ∧ c) = f (a) = 1. أيضًا، نحن f (b) ∧ f(c) = 2 ∧ 3 = 1

شعرية التوزيع:
تُسمى الشبكة L بشبكة التوزيع إذا كانت أي من العناصر a وb وc من L تفي بخصائص التوزيع التالية:
- أ ∧ (ب ∨ ج) = (أ ∧ ب) ∨ (أ ∧ ج)
- أ ∨ (ب ∧ ج) = (أ ∨ ب) ∧ (أ ∨ ج)
إذا كانت الشبكة L لا تستوفي الخصائص المذكورة أعلاه، فإنها تسمى شبكة غير توزيعية.
مثال:
- مجموعة الطاقة P (S) للمجموعة S تحت تشغيل التقاطع والاتحاد هي وظيفة توزيع. منذ،
أ ∩ (ب ∪ ج) = (أ ∩ ب) ∪ (أ ∩ ج)
وأيضًا a ∪ (b ∩ c) = (a ∪ b) ∩ (a ∪c) لأي مجموعات a وb وc من P(S). - الشبكة الموضحة في الشكل الثاني هي شبكة توزيعية. وبما أنها تحقق خصائص التوزيع لجميع الثلاثيات المرتبة المأخوذة من 1 و 2 و 3 و 4.

المكملات والشبكات المكملة:
دع L يكون شبكة محدودة مع الحد الأدنى o والحد العلوي I. دع a يكون عنصرًا إذا L. يُسمى العنصر x في L مكملاً لـ a إذا كان a ∨ x = I وa ∧ x = 0
يقال إن الشبكة L مكملة إذا كان L محددًا وكل عنصر في L له مكمل.
مثال: تحديد تكملة a و c في الشكل:

حل: تكملة أ هي د. بما أن أ ∨ د = 1 و أ ∧ د = 0
تكملة c غير موجودة. وبما أنه لا يوجد أي عنصر c مثل c ∨ c'=1 و c ∧ c'= 0.
شعرية وحدات:
تُسمى الشبكة (L, ∧,∨) بشبكة معيارية إذا كانت a ∨ (b ∧ c) = (a ∨ b) ∧ c كلما كانت a ≦ c.
المنتج المباشر للشبكات:
دع (ل 1 ∨ 1 ∧ 1 )و أنا 2 ∨ 2 ∧ 2 ) يكون شبكتين. إذن (L, ∧,∨) هو المنتج المباشر للشبكات، حيث L = L 1 س ل 2 حيث تكون العملية الثنائية ∨(الانضمام) و ∧(التقاء) على L بحيث تكون لأي (a 1 ،ب 1 ) و (أ 2 ،ب 2 ) في ل.
(أ 1 ،ب 1 )∨( أ 2 ،ب 2 )=(أ 1 ∨ 1 أ 2 ،ب 1 ∨ 2 ب 2 )
و (أ 1 ،ب 1 ) ∧ ( أ 2 ،ب 2 )=(أ 1 ∧ 1 أ 2 ،ب 1 ∧ 2 ب 2 ).
مثال: خذ بعين الاعتبار الشبكة (L, ≦) كما هو موضح في الشكل. حيث L = {1، 2}. تحديد المشابك (L 2 ، ≦)، حيث L 2 =الطول × الطول.

حل: الشباك (L 2 ، ≦) يظهر في الشكل: