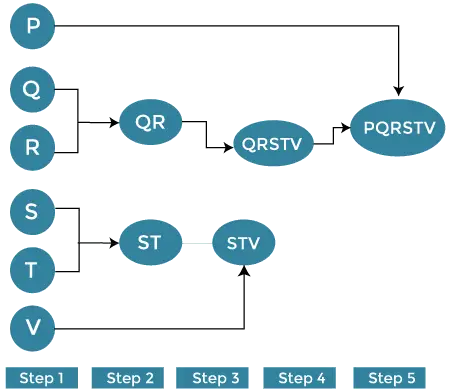
أكبر رقم في BST وهو أقل من أو يساوي k

نظرا لجذر أ شجرة البحث الثنائية وعدد صحيح ك . المهمة هي العثور على أكبر عدد في شجرة البحث الثنائية أقل من أو متساوي إلى k في حالة عدم وجود مثل هذا العنصر، اطبع -1.
أمثلة:
مدخل:

الإخراج : 21
توضيح : 19 و 25 هما أقرب رقمين إلى 21 و 19 هو أكبر عدد له قيمة أقل من أو تساوي 21.
مدخل: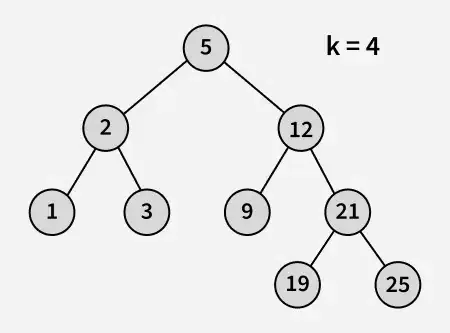
الإخراج : 3
توضيح : 3 و 5 هما أقرب رقمين إلى 4 و 3 هو أكبر رقم له قيمة أقل من أو تساوي 4.
جدول المحتويات
- [نهج ساذج] استخدام العودية - O(h) الوقت وO(h) الفضاء
- [النهج المتوقع] استخدام التكرار - O(h) Time وO(1) Space
[نهج ساذج] استخدام العودية - O(h) الوقت وO(h) الفضاء
C++والفكرة هي أن تبدأ في جذر وقارن قيمتها بـ k . إذا كانت قيمة العقدة أكبر من k، فانتقل إلى الشجرة الفرعية اليسرى. بخلاف ذلك، ابحث عن قيمة أكبر رقم أقل من k في الشجرة الفرعية الصحيحة . إذا قامت الشجرة الفرعية الصحيحة بإرجاع -1 (مما يعني عدم وجود مثل هذه القيمة)، فقم بإرجاع قيمة العقدة الحالية. وإلا قم بإرجاع القيمة التي تم إرجاعها بواسطة الشجرة الفرعية اليمنى (لأنها ستكون أكبر من قيمة العقدة الحالية ولكنها أقل من k).
// C++ code to find the largest value // smaller than or equal to k using recursion #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int val ){ data = val ; left = nullptr ; right = nullptr ; } }; // function to find max value less than k int findMaxFork ( Node * root int k ) { // Base cases if ( root == nullptr ) return -1 ; if ( root -> data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root -> data < k ) { int x = findMaxFork ( root -> right k ); if ( x == -1 ) return root -> data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root -> left k ); } int main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node * root = new Node ( 5 ); root -> left = new Node ( 2 ); root -> left -> left = new Node ( 1 ); root -> left -> right = new Node ( 3 ); root -> right = new Node ( 12 ); root -> right -> left = new Node ( 9 ); root -> right -> right = new Node ( 21 ); root -> right -> right -> left = new Node ( 19 ); root -> right -> right -> right = new Node ( 25 ); cout < < findMaxFork ( root k ); return 0 ; }
Java // Java code to find the largest value // smaller than or equal to k using recursion class Node { int data ; Node left right ; Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int findMaxFork ( Node root int k ) { // Base cases if ( root == null ) return - 1 ; if ( root . data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { int x = findMaxFork ( root . right k ); if ( x == - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root . left k ); } public static void main ( String [] args ) { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); System . out . println ( findMaxFork ( root k )); } }
Python # Python code to find the largest value # smaller than or equal to k using recursion class Node : def __init__ ( self val ): self . data = val self . left = None self . right = None # function to find max value less than k def findMaxFork ( root k ): # Base cases if root is None : return - 1 if root . data == k : return k # If root's value is smaller # try in right subtree elif root . data < k : x = findMaxFork ( root . right k ) if x == - 1 : return root . data else : return x # If root's data is greater # return value from left subtree. return findMaxFork ( root . left k ) if __name__ == '__main__' : k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node ( 5 ) root . left = Node ( 2 ) root . left . left = Node ( 1 ) root . left . right = Node ( 3 ) root . right = Node ( 12 ) root . right . left = Node ( 9 ) root . right . right = Node ( 21 ) root . right . right . left = Node ( 19 ) root . right . right . right = Node ( 25 ) print ( findMaxFork ( root k ))
C# // C# code to find the largest value // smaller than or equal to k using recursion using System ; class Node { public int data ; public Node left right ; public Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int FindMaxFork ( Node root int k ) { // Base cases if ( root == null ) return - 1 ; if ( root . data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { int x = FindMaxFork ( root . right k ); if ( x == - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return FindMaxFork ( root . left k ); } static void Main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); Console . WriteLine ( FindMaxFork ( root k )); } }
JavaScript // JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor ( val ) { this . data = val ; this . left = null ; this . right = null ; } } // function to find max value less than k function findMaxFork ( root k ) { // Base cases if ( root === null ) return - 1 ; if ( root . data === k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { let x = findMaxFork ( root . right k ); if ( x === - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root . left k ); } let k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); console . log ( findMaxFork ( root k ));
الإخراج
21
[النهج المتوقع] استخدام التكرار - O(h) Time وO(1) Space
C++والفكرة هي أن تبدأ في جذر ومقارنة قيمتها مع ك . إذا كانت قيمة العقدة <= k قم بتحديث القيمة الناتجة إلى قيمة الجذر وانتقل إلى ملف يمين الشجرة الفرعية تنتقل إلى آخر غادر شجرة فرعية. بواسطة بشكل متكرر وبتطبيق هذه العملية على جميع العقد يمكننا تقليل المساحة اللازمة للعقد العودية كومة.
// C++ code to find the largest value // smaller than or equal to k using recursion #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int val ){ data = val ; left = nullptr ; right = nullptr ; } }; // function to find max value less than k int findMaxFork ( Node * root int k ) { int result = -1 ; // Start from root and keep looking for larger while ( root != nullptr ) { // If root is smaller go to right side if ( root -> data <= k ){ result = root -> data ; root = root -> right ; } // If root is greater go to left side else root = root -> left ; } return result ; } int main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node * root = new Node ( 5 ); root -> left = new Node ( 2 ); root -> left -> left = new Node ( 1 ); root -> left -> right = new Node ( 3 ); root -> right = new Node ( 12 ); root -> right -> left = new Node ( 9 ); root -> right -> right = new Node ( 21 ); root -> right -> right -> left = new Node ( 19 ); root -> right -> right -> right = new Node ( 25 ); cout < < findMaxFork ( root k ); return 0 ; }
Java // Java code to find the largest value // smaller than or equal to k using recursion class Node { int data ; Node left right ; Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int findMaxFork ( Node root int k ) { int result = - 1 ; // Start from root and keep looking for larger while ( root != null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } public static void main ( String [] args ) { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); System . out . println ( findMaxFork ( root k )); } }
Python # Python code to find the largest value # smaller than or equal to k using recursion class Node : def __init__ ( self val ): self . data = val self . left = None self . right = None # function to find max value less than k def findMaxFork ( root k ): result = - 1 # Start from root and keep looking for larger while root is not None : # If root is smaller go to right side if root . data <= k : result = root . data root = root . right # If root is greater go to left side else : root = root . left return result if __name__ == '__main__' : k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node ( 5 ) root . left = Node ( 2 ) root . left . left = Node ( 1 ) root . left . right = Node ( 3 ) root . right = Node ( 12 ) root . right . left = Node ( 9 ) root . right . right = Node ( 21 ) root . right . right . left = Node ( 19 ) root . right . right . right = Node ( 25 ) print ( findMaxFork ( root k ))
C# // C# code to find the largest value // smaller than or equal to k using recursion using System ; class Node { public int data ; public Node left right ; public Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int FindMaxFork ( Node root int k ) { int result = - 1 ; // Start from root and keep looking for larger while ( root != null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } static void Main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); Console . WriteLine ( FindMaxFork ( root k )); } }
JavaScript // JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor ( val ) { this . data = val ; this . left = null ; this . right = null ; } } // function to find max value less than k function findMaxFork ( root k ) { let result = - 1 ; // Start from root and keep looking for larger while ( root !== null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } let k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); console . log ( findMaxFork ( root k ));
الإخراج
21إنشاء اختبار