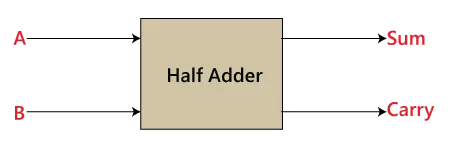
يعد Half-Adder لبنة أساسية لإضافة رقمين كمدخلين وإنتاج مخرجين. يتم استخدام المُجمِع لإجراء عملية OR لرقمين ثنائيين فرديين. ال أنها تزيد و ملحق البتات هي حالتان من حالات الإدخال، و 'يحمل ' و 'مجموع 'هما حالتان من حالات الإخراج لنصف الأفعى.

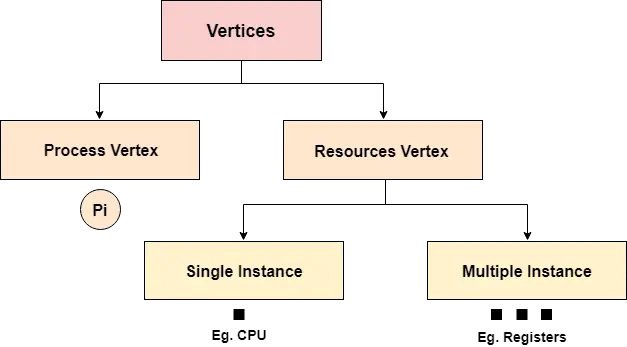
مخطط الكتلة

جدول الحقيقة

في الجدول أعلاه،

1. 'A' و'B' هما حالتا الإدخال، و'sum' و'carry' هما حالتا الإخراج.
2. ويكون خرج الحمل 0 في حالة عدم وجود كلا المدخلين 1.
3. يتم تحديد البت الأقل أهمية من المجموع بواسطة بت 'المجموع'.

نموذج SOP للمبلغ والحمل هو كما يلي:

المجموع = س'ص+ص'
احمل = س ص

بناء دائرة نصف الأفعى:

في المخطط الهيكلي، رأينا أنه يحتوي على مدخلين ومخرجين. ال أنها تزيد و ملحق البتات هي حالات الإدخال، و يحمل و مجموع هي حالات الإخراج للنصف الأفعى. تم تصميم نصف الأفعى بمساعدة البوابتين المنطقيتين التاليتين:

1. 2-المدخل والبوابة.
2. 2-مدخل بوابة حصرية OR أو بوابة Ex-OR

1. بوابة OR حصرية أو بوابة Ex-OR ذات مدخلين

ال مجموع يتم إنشاء البت بمساعدة حصري أو أو السابق أو بوابة.

ما ورد أعلاه هو رمز EX-OR بوابة. في الرسم البياني أعلاه، 'A' و'B' هما المدخلان، و'SUMOUT' هي النتيجة النهائية بعد إجراء عملية XOR لكلا الرقمين.

جدول الحقيقة لبوابة EX-OR هو كما يلي:

يتضح من الجدول أعلاه أن بوابة XOR تعطي النتيجة 1 عندما يكون كلا المدخلين مختلفين. عندما يكون كلا المدخلين متماثلين، فإن XOR يعطي النتيجة 0. لمعرفة المزيد حول بوابة XOR، انقر هنا.

2. 2-المدخل والبوابة:

بوابة XOR غير قادرة على إنشاء بتة الحمل. ولهذا الغرض نستخدم بوابة أخرى تسمى AND Gate. بوابة AND تعطي النتيجة الصحيحة للحمل.

ما ورد أعلاه هو رمز و بوابة. في الرسم البياني أعلاه، 'A' و'B' هما المدخلان، و'OUT' هي النتيجة النهائية بعد تنفيذ وتشغيل كلا الرقمين.

يوجد جدول الحقيقة التالي للبوابة AND:

يتضح من الجدول أعلاه أن بوابة AND تعطي النتيجة 1 عندما يكون كلا المدخلين 1. عندما يكون كلا المدخلين مختلفين و0، فإن بوابات AND تعطي النتيجة 0. لمعرفة المزيد حول بوابة AND، انقر هنا .

الدائرة المنطقية النصفية:

لذلك، تم تصميم Half Adder من خلال الجمع بين بوابات 'XOR' و'AND' وتوفير المبلغ والحمل.

هناك ما يلي تعبير منطقي ل دائرة نصف الأفعى :

المجموع= أ XOR ب (أ+ب)

احمل= أ وب (أ.ب)